Fizyka II OO/Ćwiczenia III: Prąd przesunięcia oraz obwód drgający LC
Zadania do rozwiązania na ćwiczeniach
Zad.1
Wychodząc od równania [math] I_{przesunięcia} = \epsilon_{0} A \frac{dE}{dt} [/math] przedstaw zależność pomiędzy natężeniem prądu przesunięcia w kondensatorze płaskim a pojemnością C oraz prędkością zmian różnicy potencjałów pomiędzy okładkami.
Zad.2
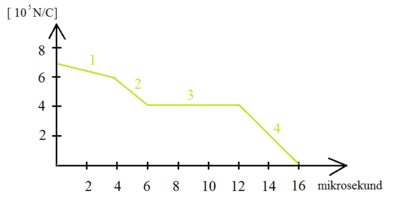
Natężenie jednorodnego pola elektrycznego zmienia się zgodnie z przedstawionym wykresem. Jaka jest wartość [math] I_{przesunięcia} [/math] (w zaznaczonych 4 przedziałach czasowych), który płynie przez prostopadłą do kierunku pola powierzchnię o polu 1,13 [m²]?
Zad.3
Przeprowadź analizę dwóch analogicznych układów drgających: mechanicznego - klocek i sprężyna oraz elektrycznego układ LC.
Zad.4
Całkowita energia pewnego obwodu drgającego LC wynosi 115 [μJ], zaś maksymalny ładunek na okładkach kondensatora jest równy 1,19 [μC]. Oblicz pojemność takiego obwodu.
Zad.5
Ile wynosi okres oraz częstość drgań obwodu drgającego LC, w którym energia elektryczna na kondensatorze zmienia się na energię magnetyczną w cewce w ciągu 1,85 [μs]? Ile czasu wymaga zmiana energii magnetycznej maksymalnej w minimalną?
Zad.6
Ile czasu zajmie kondensatorowi (w obwodzie drgającym LC) ponowne naładowanie, jeśli w momencie początkowym natężenie prądu miało wartość maksymalną? Przyjmij, że L = 40 [mH] oraz C = 3,5 [μF].
Zadania domowe
Zad. 1
Wyznacz maksymalną wartość natężenia prądu w obwodzie drgającym LC, w przypadku gdy L = 1,3 [mH], C = 5 [μF] zaś maksymalny ładunek na okładkach kondensatora wynosi 3 [μC].
Zad. 2
Wyznacz maksymalną wartość natężenia prądu w obwodzie drgającym LC, w przypadku gdy L = 80 [mH], C = 4,1 [μF]. Jaka będzie całkowita energia w obwodzie jeśli maksymalny ładunek na okładkach kondensatora wynosi 3,2 [μC].
Zad. 3
W chwili początkowej dodatni ładunek na jednej z okładek kondensatora osiąga wartość maksymalną. Ile musi upłynąć czasu, aby ładunek dodatni na tej okładce znów osiągnął maksimum? Ile musi upłynąć czasu, aby indukcja magnetyczna pola w cewce osiągnęła wartość maksymalną? Przyjmij, że częstość drgań omawianego obwodu wynosi 280 [Hz].