Fizyka II OO/Ćwiczenia VI: Załamanie światła na granicy ośrodków

Z Brain-wiki

Zadania do rozwiązania na ćwiczeniach

Zad.1
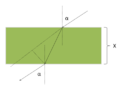
Proszę obliczyć wartości kątów: [math]\alpha_{4}[/math] i [math]\alpha_{5}[/math]. Przyjmij, że początkowo światło pada na powierzchnię graniczną między dwoma przezroczystymi ośrodkami pod kątem [math]\alpha_{0}[/math] = 38,9 [°].


Zad.2
Twierdzenie: promień światła padający na powierzchnię szklanej płytki o pewnej grubości X przechodzi przez nią nie zmieniając kierunku. Obserwuje się jedynie pewne przesunięcie, zobrazowane na rysunku. Proszę udowodnić to twierdzenie oraz wyprowadzić wzór na to przesuniecie dla bardzo małych kątów padania (w przypadku, gdy promień pada prawie prostopadle).


Zad.3
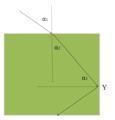
Jaką minimalną wartość współczynnika załamania światła posiada materiał, z którego zbudowana jest sztabka, jeśli w punkcie Y promień świetlny doznaje całkowitego wewnętrznego odbicia?


Zad.4
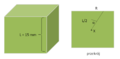
Posiadasz pewien sześcian wykonany z materiału o współczynniku załamania 1,38, który jest uszkodzony dokładnie w samym środku. Proszę obliczyć, ile procent całkowitej powierzchni bryły musi zostać zasłonięty, aby uszkodzenie było niewidoczne. Zakładamy, że każda z krawędzi kostki ma długość 15 [mm].


  • Rysunek do zadania 1

  • Rysunek do zadania 2

  • Rysunek do zadania 3

  • Rysunek do zadania 4

Zadania domowe

Zad.1
Jaki współczynnik załamania charakteryzuje sześcian o wymiarach 0,93 [m] (wysokość) na 1,2 [m] (szerokość), jeśli obserwator patrzą z poziomu górnej powierzchni widzi widzi dolną krawędź Y na skraju obrazu sześcianu?


Zad.2
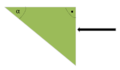
Promień światła pada na pryzmat pod kątem prostym do jeden ze ścian (tak jak to przedstawiono na rysunku). Współczynnik załamania materiału, z którego zbudowany jest pryzmat wynosi 1,49. Jaka jest największa wartość kąta, przy którym nastąpi całkowite wewnętrzne odbicie promienia świetlnego? Zakładamy, że eksperyment przeprowadzany jest w warunkach domowych, a zatem pryzmat otoczony jest powietrzem. Jak zmieni się wartość tego kąta, jeśli umieścimy pryzmat w alkoholu etylowym o współczynniku załamania 1,37?


Zad.3
Który z ośrodków ma największy, a który największy współczynnik załamania?


  • Rysunek do zadania 1

  • Rysunek do zadania 2

  • Rysunek do zadania 3

Źródło: „http://brain.fuw.edu.pl/edu/index.php?title=Fizyka_II_OO/Ćwiczenia_VI:_Załamanie_światła_na_granicy_ośrodków&oldid=2398”