Fizyka I FM/Dynamika w układach inercjalnych i nieinercjalne
Zadanie 1
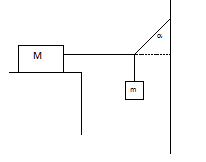
Układ pokazany na rysunku 1 jest w równowadze, ale zaczyna się poruszać jeśli jakakolwiek dodatkowa masa zostaje dołożona do ciężarka m=5 kg. Jaki jest współczynnik tarcia statycznego pomiędzy klockiem o masie M=10kg a płaszczyzną na której on spoczywa.
Zadanie 2
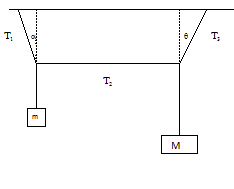
Układ pokazany na rysunku 2 jest w równowadze i sznurek w centrum jest dokładnie poziomo. Znaleźć naprężenia [math]T_1[/math], [math]T_2[/math], [math]T_3[/math] oraz kąt [math]\Theta[/math] jeśli znane są masy m, M oraz kąt [math]\alpha[/math].
Zadanie 3
Po równi pochyłej o kącie nachylenia [math]\alpha[/math] zsuwa się klocek. Zależność przebytej drogi do czasu dana jest wzorem [math]x(t)=A+Bt+Ct^2[/math], gdzie A,B,C — stałe. Oblicz współczynnik tarcia klocka o równie.
Zadanie 4
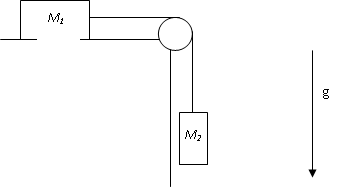
Dwie masy [math]M_1[/math] i [math]M_2[/math] są połączone nierozciągliwą giętką lina o zaniedbywanie małej masie. Masa [math]M_1[/math] leży na poziomym stole i może się po nim poruszać doznając siły tarcia ze współczynnikiem tarcia poślizgowego równym f. Masa [math]M_2[/math] zwisa na linie poza krawędzią stołu (patrz rysunek 3.). Zakładając, że na linę nie działa siła tarcia ani od powierzchni stołu, ani od krawędzi oblicz przyspieszenie w ruchu tych mas pod wpływem siły ciężkości. Zakładamy, że w czasie ruchu mas lina jest naprężona. Ile wynosi naprężenie liny? Przyśpieszenie grawitacyjne wynosi g. Przedyskutuj możliwe rozwiązania w zależności od początkowej prędkości ruchu masy [math]M_1[/math] (zakładamy, że kierunek tej prędkości początkowej może być tylko wzdłuż naprężonej liny). Zakładamy też, że obie części liny są prostopadłe do krawędzi stołu.
Zadanie 5
Oscylatorem harmonicznym nazywamy punkt materialny, który wykonuje drgania pod wpływem siły zwrotnej [math]F(x)=-kx[/math]. Zapisz równanie ruchu oscylatora harmonicznego. Rozwiąż to równanie (wyznacz [math]x(t)[/math]) oraz korzystając z pochodnej oblicz prędkość i przyśpieszenie oscylatora.
Zadanie 6
Swobodnie spadający kamień o masie m wpada do studni z prędkością początkową [math]V_0[/math]. Zakładamy, że w wodzie działa siła oporu. Znaleźć równanie położenia, prędkości oraz przyśpieszenia w zależności od czasu.
Zadanie 7
W windzie znajduje się waga sprężynowa (dynanometr). Jakie są jej wskazania dla masy m w przypadku, gdy winda jedzie:
- z przyspieszeniem a skierowanym do góry,
- ruchem jednostajnym,
- z przyspieszeniem a skierowanym w dół.
Zadanie 8
W wagonie, który porusza się z przyspieszeniem [math]a[/math] po prostym torze poziomym znajduje się równia nachylona pod kątem α do poziomu. Na równi leży ciało o masie m.
- Jakie powinno być przyśpieszenie ao wagonu, aby ciało nie zsuwało się z równi, jeżeli nie ma siły tarcia?
- Jaką siłą nacisku N ciało działa na równie? Jak porusza się ziało względem wagonu, jeżeli wagon jedzie z przyśpieszeniem: [math]a \gt a_{0} [/math], [math]a \lt a_{0}[/math].
Zadanie 9
W samochodzie cysternie jest przewożona woda. O jaki kat odchyli się poziom cieczy w chwili gdy samochód zacznie hamować z opóźnieniem [math]\unit{5 }{m/s^{2}}[/math]?
Zadanie 10
Dwaj myśliwi polowali na wilki w Bieszczadach. Pierwszy myśliwy oddał strzał w kierunku zachodnim od siebie, drugi – w kierunku południowym. Oba strzały były nie celne. Myśliwi tłumaczyli swoje niepowodzenie istnieniem siły Coriolisa. Czy ich uzasadnienie było słuszne? Oblicze odchylenia toru pocisku będące skutkiem siły Coriolisa, jeżeli średnia prędkość lotu [math]V_0[/math]=300m/s, czas lotu t = 1 s, a szerokość geograficzna [math]\phi=49^0[/math].