Fizyka I FM/Kinematyka2
Wstęp
Ruch po okręgu jest najprostszym przypadkiem płaskich ruchów krzywoliniowych. W ogólnym przypadku ruch po okręgu opisujemy równaniami:
gdzie:
[math]\phi(t)[/math] — dowolna funkcja czasu.
Ruch odbywa się po okręgu o środku w punkcie [math](x_0, y_0)[/math] i promieniu [math]\rho[/math].
co sprowadza się do równania:
jeśli środek okręgu znajduje się w punkcie (0,0).
Ruch po okręgu w kartezjańskim układzie współrzędnych
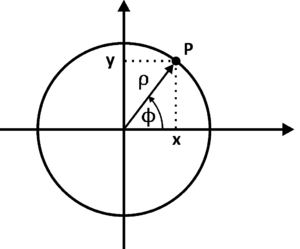
Współrzędne punktu P poruszającego się po okręgu można wyrazić w następujący sposób (patrz rysunek %i 1):
Wprowadzimy teraz następujące wielkości:
Prędkość kątowa
Przyspieszenie kątowe
Ruch po okręgu — opis
Dla ruchu po okręgu mamy więc:
- Współrzędne punktu P:
[math]\left\{\begin{array}{l} x(t)=\rho\cos(\alpha(t))\\ \\ y(t)=\rho\sin(\alpha(t)) \end{array}\right. [/math]
- Prędkość wzdłuż osi x i y kartezjańskiego układu współrzędnych:
[math]\left\{\begin{array}{rcccccl} V_x(t)&=&\frac{dx(t)}{dt}&=&-\frac{d\alpha(t)}{dt}\cdot\frac{d}{dt}(\rho\cos(\alpha(t)))&=& -\omega \rho\sin(\alpha(t))\\[5pt] V_y(t)&=&\frac{dy(t)}{dt}&=&\frac{d\alpha(t)}{dt}\cdot\frac{d}{dt}(\rho\sin(\alpha(t)))&=& \omega \rho\cos(\alpha(t))\\ \end{array}\right. [/math]
- Przyspieszenie liniowe wzdłuż osi x i y kartezjańskiego układu współrzędnych:
[math] \left\{\begin{array}{rcl} a_x&=&\frac{dV_x(t)}{dt}= -\omega^2\rho\cos(\alpha(t))-\epsilon \rho\sin(\alpha(t))\\ \\ a_y&=&\frac{dV_x(t)}{dt}= -\omega^2\rho\sin(\alpha(t))+\epsilon \rho\cos(\alpha(t))\\ \end{array}\right. [/math]
Ruch po okręgu w biegunowym układzie współrzędnych
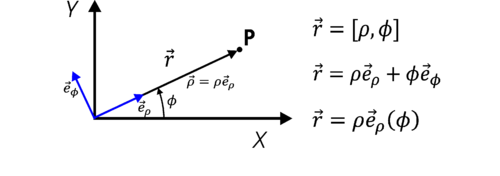
Czasem wygodniej jest opisać ruch w biegunowym układzie współrzędnych (patrz rysunek %i 2). Zanim opiszemy ruch po okręgu w tym układzie, zauważmy związki jakie zachodzą pomiędzy współrzędnymi układu kartezjańskiego i biegunowego:
Wersory [math](\vec{e}_\rho,\vec{e}_\phi)[/math] układu biegunowego, w układzie kartezjańskim można zapisać w następujący sposób:
Wektor położenia punktu w płaskim układzie kartezjańskim można wyrazić w następujący sposób:
Podstawiając zależności pomiędzy współrzędnymi kartezjańskim i i biegunowymi dostajemy następujący wzór na wektor położenia:
Z kolei wektor prędkości w układzie kartezjańskim:
Podobnego przejścia z układu kartezjańskiego do biegunowego możemy dokonać również dla przyspieszenia:
Zauważmy, iż w przypadku ruchu po okręgu w układzie biegunowym wektor prędkości ma tylko jedną składową, prostopadłą do wektora wodzącego [math]\rho[/math]:
natomiast przyspieszenie ma dwie składowe:
- składową styczną do toru, nazywaną przyspieszeniem transersalnym:
[math]\vec{a}_s=\epsilon\rho\vec{e}_\phi [/math]
- składową równoległą do wektora wodzącego [math]\vec{\rho}[/math], nazywaną przyspieszeniem radialnym:
[math] \vec{a}_r=-\omega^2\rho\vec{e}_\rho [/math]
Ruch jednostajny po okręgu
Rozważymy teraz ruch po okręgu, który odbywa się ze stałą prędkością liniową [math]V[/math]. W przypadku ruchu jednostajnego prostoliniowego, wektor prędkości zachowywał stały kierunek w przestrzeni oraz stałą wartość. Ruch po okręgu jest przypadkiem ruchu krzywoliniowego, w którym wartość wektora prędkości (długość tego wektora) może być zachowana, zmienia się natomiast jego kierunek. Mówiąc zatem o ruchu jednostajnym po okręgu, zakładamy, że nie ulega zmianie wartość prędkości w tymże ruchu. W poprzednim rozdziale pokazaliśmy, iż w przypadku ruchu po okręgu opisywanego w układzie biegunowym prędkość można wyrazić następującym wzorem:
Skoro z założenia wartość wektora prędkości ma być stała [math](\vec{V}=const)[/math], to widzimy, że również wyrażenie [math]\omega\rho[/math] musi mieć stałą wartość. Stały jest również promień okręgu [math]\rho[/math], w związku z czym stała jest także prędkość kątowa [math]\omega[/math]. Przyspieszenie kątowe [math]\epsilon[/math] jest pochodną prędkości kątowej po czasie:
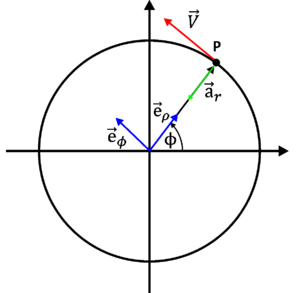
Jak wiemy z kursu matematyki, pochodna wektora stałego jest równa 0, a zatem w przypadku ruchu jednostajnego po okręgu, kiedy to [math]\omega=const[/math], przyspieszenie kątowe [math]\epsilon = 0[/math]. Wiadomo, że przyspieszenie w ruchu po okręgu w układzie biegunowym ma dwie składowe, (równania (%i 17 i (%i 19)), jednakże z uwagi na zerową wartość przyspieszenia kątowego [math]\epsilon[/math], składowa styczna wektora przyspieszenia (wzór (%i 17) znika i pozostaje tylko i wyłącznie składowa radialna (patrz rysunek %i 3).
Ruch jednostajny po okręgu jest przykładem ruchu harmonicznego, co prześledzimy powracając z opisem ruchu do układu kartezjańskiego. Analogicznie jak w przypadku drogi pokonywanej przez ciało w ruchu jednostajnie prostoliniowym, w przypadku ruchu jednostajnego po okręgu, w którym stała jest wartość wektora prędkości, przyrost zakreślanego przez punkt P kąta [math]\phi[/math] można zapisać następującym wyrażeniem:
podstawiając powyższy wzór do wzorów (%i 8), (%i 8) i (%i 9) dostajemy (przypominamy, że we wzorze (%i 9 na przyspieszenie liniowe, przyspieszenie kątowe [math]\epsilon[/math] ma wartość 0):
Przyspieszenie liniowe wzdłuż osi x i y kartezjańskiego układu współrzędnych:
Jak widzimy zarówno położenie punktu, wartość i kierunek jego prędkość oraz przyspieszenie zmieniają się periodycznie z okresem: