Fizyka I FM/Ruch w polu siły centralnej

Zadanie 1.

Cząstka o masie m i energii E znajduje się w polu siły jednowymiarowego oscylatora harmonicznego: F=−kx. Wyznacz i narysuj potencjał tej siły. Scharakteryzuj punkty przestrzeni dostępne cząstce w trakcie jej ruchu . Przedyskutuj ruch tej cząstki w zależności od jej energii.

Zadanie 2.

Przedyskutuj ruch cząstki o masie m i energii E_p w polu o energii potencjalnej:
[math]E_{p}(x)= \begin{cases} A(|x-a|-a),\ \textrm{dla}\ x\geq 0 \\ 0,\ \textrm{dla}\ x\lt 0 \\ \end{cases} [/math]

Zadanie 3.

Punkt o masie m porusza się pod wpływem siły centralnej po okręgu o promieniu R, który przechodzi przez centrum siły, jak zależy zawartość siły od odległości od centrum, wiedząc iż wartość moment pędu wynosi L.

Zadanie 4.

W filmie „Armagedon” z 1998r. zespół geologów mających wysadzić w powietrze kometę, zostaje wyposażony w specjalne kombinezony, które za pomocą silniczków rakietowych dociskają astronautę do powierzchni komety. Tego typu kombinezony miały zabezpieczyć geologa przed jego wejściem na orbitę wokół komety lub odlotem w przestrzeń kosmiczną np. gdyby wykonał silny skok w górę. Sprawdź sensowność takiego uzasadnienia. Przyjmij, że masa komety wynosi [math]M_k=\unit{10^{15}}{kg}[/math], promień komety [math]R_k = \unit{8}{km}[/math], masa Ziemi [math]M_z =\unit{ 6\cdot10^{24}}{kg}[/math], promień Ziemi [math]R_z = \unit{6400}{km}[/math], stała grawitacji [math]\textrm{G}=\unit{6,67\cdot10^{-11}}{\frac{m^3}{kg\cdot s^2}}[/math], rekord świata w skoku wzwyż [math]h = \unit{2,45}{m}[/math].

Zadanie 5.

Przyjmując, że kometa z zadania 4 porusza się wokół Słońca po orbicie eliptycznej, a dużej półosi a 10 razy większej od półosi orbity Ziemi, oblicz okres jej obiegu w latach.

Zadanie 6.

Przyjmując, że kometa z zadania 4 obraca się wokół własnej osi w czasie [math]T = \unit{8}{h}[/math], oblicz, na jakiej wysokości, trzeba umieścić satelitę, który ma stale znajdować się nad określonym obszarem tej komety. (W przypadku Ziemi, orbita, po której poruszający się satelita stale znajduje się nad tym samym punktem Ziemi, nazywana jest orbitą geostacjonarną).

Materiały uzupełniające do ćwiczeń

Ciała w polu o potencjale: [math]V=-\frac{\alpha}{r}[/math], gdzie r jest odległością ciała od centrum siły, poruszają się po krzywych stożkowych. Ogólna postać takiej krzywej we współrzędnych biegunowych jest następująca:

[math]r(\phi)=\frac{p}{1+ecos(\phi)}[/math]

gdzie:

• p jest tzw. parametrem orbity,
• e jest mimośrodem orbity,
  
• r i φ to współrzędne, określające położenie ciała.

W przypadku potencjału pola grawitacyjnego: [math]V=-\frac{GM}{r}[/math], związki pomiędzy masą ciała m, które porusza się w polu ciała o masie M (przy czym [math]m\lt \lt M[/math], jego momentem pędu L i energią całkowitą E, a parametrem orbity oraz jej mimośrodem są następujące:

• [math]p=\frac{L^2}{GMm^2}[/math]
  
  
• [math]e=\sqrt{1+\frac{2EL^2}{GM^2m^3}}[/math]
  

W przypadku gdy całkowita energia ciała jest ujemna ([math]E\lt 0[/math]), wówczas mimośród [math]e\lt 1[/math] i tor ruchu jest elipsą, które we współrzędnych kartezjańskich ma postać:

[math]\frac{x^2}{a}+\frac{y^2}{b}=1[/math]

Elipsa we współrzędnych kartezjańskich. O — środek układu współrzędnych oraz środek elipsy;F, F’ — ogniska elipsy, w jednym ognisk głównych znajduje się ciało o masie M, będące źródłem pola grawitacyjnego, na powyższym rysunku przyjęto, że jest to ognisko — F, a, b — odpowiednio duża i mała półoś elipsy, c' — odległość ognisk od środka elipsy, r, φ — współrzędne ciała w układzie biegunowym.

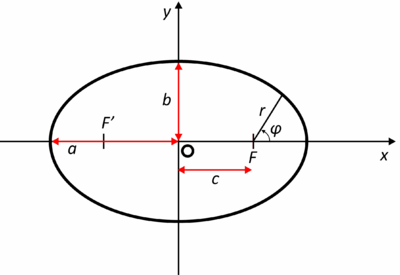
Na rysunku %i 1 możemy zauważyć proste związki geometryczne:

[math]c=a^2-b^2[/math], [math]e=\frac{c}{a}=\sqrt{1-\frac{b^2}{a}}[/math]

z kolei, półosie elipsy a i b są powiązane z parametrami orbity p:

[math]p=\frac{b^2}{a}[/math]

Całkowita energia kinetyczna ciała w ruchu po orbicie zamkniętej w polu grawitacyjnym jest równa:

[math]E=-\frac{GMm}{2a}[/math]

Ciekawe zagadnienia

Zagadnienie 1.

Podczas przelotu satelity szpiegowskiego obserwowano go od zenitu do punktu wschodu na horyzoncie. Przyjmując, że satelita poruszał się po okręgu, na wysokości [math]h=\unit{1000}{km}[/math], oblicz jak długo trwał obserwowany przelot. Przyjmij, że promień Ziemi wynosi [math]R=\unit{6400}{km}[/math], zaś przyspieszenie ziemskie tuż przy powierzchni Ziemi wynosi [math]\textrm{g} = \unit{10}{\frac{m}{s^2}}[/math].

Zagadnienie 2.

W dniu 18 marca 1965 roku w statku kosmicznym Woschod 2 zostali wyniesieni na orbitę dwaj astronauci — Aleksy Leonow oraz Paweł Bielajew. Celem misji było pierwsze w historii wyjście człowieka w otwartą przestrzeń kosmiczną. Eksperyment się udał, chociaż nie obyło się bez sporych problemów. Po 12 minutowym pobycie Leonowa w przestrzeni kosmicznej, w trakcie jego wchodzenia z powrotem do kapsuły, Woschod został wprawiony w ruch obrotowy oraz utracił orientację względem Słońca i Ziemi. W zaistniałej sytuacji statek nie mógł wejść na orbitę schodzącą w kierunku Ziemi. Jedynym wyjściem ratującym życie astronautom było samodzielne ustawienie statku względem punktów orientacyjnych oraz samodzielne obliczenie parametrów schodzenia z orbity. W ciągu 43 minut, przy pomocy kartki, ołówka i suwaka logarytmicznego, astronauci dokonali niezbędnych obliczeń. W wyznaczonym przez nich momencie, zostały uruchomione silniki hamujące. Astronauci szczęśliwie powrócili na Ziemię, chociaż nie obyło się bez dalszych przygód. Drobny błąd spowodował iż wylądowali 3000 km od zaplanowanego miejsca, a ich kapsuła wpadła idealnie pomiędzy trzy syberyjskie sosny, z których jedna zasłaniała wyjście. Kiedy w końcu udało im się z niej wydostać na zewnątrz, musieli zaraz wrócić do środka statku. Na zewnątrz bowiem panował siarczysty mróz, śnieg sięgał astronautom do pasa, a do tego pojawiły się wilki i niedźwiedzie, zainteresowane co spadło z kosmosu do jedzenia. Po dwóch dniach, astronauci zostali odnalezieni przez ekipę ratunkową, która po następnych kliku godzinach spędzonych na wypłaszaniu natrętnych niedźwiedzi, zabrała astronautów do domu. Poniższe zadanie jest bardzo uproszczoną próbą odtworzenia lądowania.

Po orbicie kołowej, na wysokości h = 400 km nad Ziemią krąży załogowy statek kosmiczny. W momencie kiedy statek znajduje się nad miejscowością A, zostają włączone silniki hamujące, celem sprowadzenia statku na Ziemię.

• Pozycja na liście punktowanej
• Oblicz parametry orbity, po której statek zbliża się w kierunku Ziemi (krzywa narysowana linią przerywaną), jeśli astronauci mają wylądować na poligonie (punkt B), oddalonym o d = 3200 km od miejscowości A.
• Oblicz prędkość statku tuż przed zetknięciem z Ziemią.

Przyjmij, że promień Ziemi [math]R = \unit{6400}{km}[/math], jej masa [math]M = \unit{6\cdot10^{24}}{kg}[/math], stała grawitacji [math]\textrm{G}=\unit{6,67\cdot10^{-11}}{\frac{m^3}{kg\cdot s^2}}[/math], wartość przyspieszenia Ziemskiego [math]\textrm{g} = \unit{10}{\frac{\textrm{m}}{s^2}}[/math].