Fizyka I FM/Zasada zachowania energii

Zadanie 1

Lekkoatleta rzucający młotem, rozpędza młot przed puszczeniem wykonując wspólnie z nim kilka obrotów. Podaj na tym przykładzie jakie to siły: odśrodkowa i dośrodkowa. Wiedząc, że rekord świata długości rzutu wynosi D = 86,7 m, a masa młota wynosi M = 7,257 kg, oblicz wektor pędu młota w chwili puszczenia w tym rekordowym rzucie. Rzut ukośny młota nastąpił pod optymalnym kątem ze względu na zasięg rzutu — podaj jakim. Zakładamy, że młot został rzucony z wysokości pomijalnie małej nad poziomem stadionu. Przyspieszenie grawitacyjne wynosi [math]g=\unit{9,81}{\frac{m}{s^2}}[/math]. Masę linki młota można pominąć jako małą. Porównaj liczbowo wartość pędu nadanego kuli z pędem piechura o masie 75 kg maszerującego z prędkością [math]\unit{4,5}{\frac{km}{h}}[/math].

Zadanie 2

Spoczywająca kulka o masie m w pewnej chwili czasu zaczyna swobodnie spadać w jednorodnym, stałym polu grawitacyjnym o natężeniu g. Jej tor jest opisany równaniami x=L=const oraz z=0, a przyśpieszenie kulki opisuje wektor [math] \vec{g}=[0,-g,0][/math]. Znajdź moment pędu kulki względem początku układu współrzędnych w dowolnej chwili czasu. Wyznacz moment siły działający na kulkę względem początku układu współrzędnych i pokaż, że zasada dynamiki [math]\vec{M}=\lim_{\Delta t \to \infty} \frac{\Delta \vec{J}}{\Delta t}[/math] prowadzi do poprawnego wyniku.

Zadanie 3

Ogrodnik o masie M siedzi na lekkiej (przyjmujemy, że nieważkiej) huśtawce i podlewa trawnik kierując strumień wody z cienkiego elastycznego węża poziomo na wprost przed siebie. Huśtawka może się odchylać w płaszczyźnie poruszania się wody. Policzyć siłę odrzutu działającą na ogrodnika oraz kąt odchylenia huśtawki od pionu jeśli prędkość strumienia wody wynosi U, przepływ wody (czyli jej objętość wylatująca z końcówki węża w ciągu jednostki czasu) wynosi J (liczone np. w [math]\unit{}{\frac{{cm}^3}{s}}[/math]), a gęstość wody wynosi ρ. Przyspieszenie grawitacyjne wynosi g.

Zadanie 4

Dwóch mężczyzn stoi na zamarzniętym stawie w odległości 20 m. Jeden z nich waży 60 kg, a drugi 90 kg. Pomiędzy nimi (w połowie drogi) stoi kubek z gorącą herbatą. Panowie ciągną za końce cienkiej linki tak, że jest ona cały czas napięta. Jak daleko i w jakim kierunku przesunie się lżejszy z panów,jeżeli cięższy przesunął się w kierunku kubka o 6 m.

Zadanie 5

Masa Ziemi wynosi [math]m_Z=\unit{5,98\cdot {10}^{24}}{ kg}[/math], masa Księżyca [math]m_K=\unit{7,35\cdot {10}^{22}}{ kg}[/math], średnia odległość między Ziemią a Księżycem [math]d=\unit{3,82\cdot {10}^5}{km}[/math], a okres obiegu Księżyca wokół Ziemi [math]T=\unit{2,36\cdot {10}^6}{s}[/math]. Policz moment pędu układu Ziemia — Księżyc względem jego środka masy.

Zadanie 6

Rakieta znajduje się w przestrzeni kosmicznej, daleko od planet. W pewnej chwili zostały włączonej jej silniki. W pierwszej sekundzie odrzutu (ognia), rakieta wyrzuciła 1/120 swojej masy ze względną prędkością [math]\unit{2400}{\frac{m}{s}}[/math].

1. Jakie było początkowe przyspieszenie rakiety?
2. Załóż, że [math]\frac{3}{4}[/math] początkowej masy rakiety to paliwo, które jest spalane w stałym tempie. Policz, jaka będzie prędkość rakiety, jeżeli rakieta początkowo spoczywała, a całe paliwo uległo spaleniu po [math]\unit{90}{s}[/math].

Zadanie 7

Na lince o długości l zawieszono ciężarek o masie m i odchylono z położenia równowagi o kąt α=30[math]^\textrm{o}[/math], a następnie puszczono. Wyznacz siłę naprężenia linki, gdy linka tworzy z pionem dowolny kąt β (β [math]\leq[/math]30[math]^\textrm{o}[/math]).

Zadanie 8

Z górki o wysokości h i kącie nachylenia do poziomu α zjeżdża na sankach chłopiec. W jakiej odległości od podnóża górki zatrzymają się sanki, jeśli współczynnik tarcia między śniegiem a sankami jest na całej drodze taki sam i wynosi f ?

Zadanie 9

Ilustracja do zadania 3.

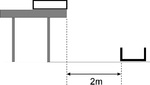
Dwoje dzieci strzela ze sprężynowego pistoletu umieszczonego na stole do pudełka, o podstawie 20x20 cm, umieszczonego na podłodze i oddalonego w poziomie o 2 m od brzegu stołu (Rys.%i 1). Jedno dziecko ścisnęło sprężynę o 1 cm i kulka upadła 20 cm przed pudełkiem. Jak powinno ścisnąć tę sprężynę drugie dziecko, aby ta sama kulka wpadła do pudełka? Zaniedbać wysokość pudełka.

Zadanie 10

Trzy kule o jednakowych średnicach i masach [math]m_1[/math], [math]m_2[/math], [math]m_3[/math] umieszczono w poziomej rynnie, w której mogą poruszać się bez tarcia. Kuli 1 nadano prędkość [math]v_1[/math] w kierunku spoczywających kul 2 i 3. Kule 2 i 3 nie dotykają się. Zakładając, że zderzenia są doskonale sprężyste policzyć prędkości kul po zderzeniach.

Zadanie 11

Cząsteczka gazu mająca prędkość v zderza się sprężyście z drugą taką samą cząsteczką, która początkowo spoczywa. Po zderzeniu pierwsza cząsteczka porusza się pod kątem 30[math]^{\textrm{o}}[/math] do pierwotnego kierunku ruchu. Znajdź wektor prędkosci każdej cząsteczki po zderzeniu i kąt, jaki tworzy odrzucona cząsteczka z kierunkiem pierwotnym cząsteczki padającej.