
Fizyka I OO/Wykład II
Pojęcia i wielkości fizyczne wprowadzane na wykładzie:
- punkt materialny,
- układ odniesienia,
- tor ruchu,
- prędkość chwilowa,
- prędkość średnia,
- przyspieszenie,
- droga,
- wektor położenia.
Pokazy
- Analiza ruchu jednostajnego i jednostajnie przyspieszonego prostoliniowego na torze powietrznym z użyciem programu komputerowego
- Ruch po okręgu, kierunek prędkości w tym ruchu.
Klasyfikacja ruchów
- ze względu na kształt toru: prostoliniowe i krzywoliniowe
- ze względu na zmianę prędkości: jednostajny, jednostajnie zmienny, niejednostajnie zmienny.
Układ odniesienia
ciało względem którego opisuje się ruchu.
Ruch dowolnego ciała można opisywać korzystając z modelu punktu materialnego. Model ten może być użyty, jeśli w opisywanym zjawisku rozmiary ciała nie odgrywają żadnej roli. Realne gabaryty przedmiotu nie mają znaczenia. Model ten, jak każdy model w fizyce, ma granice stosowalności.
Z układem odniesienia związuje się układ współrzędnych. Jednym z nich jest kartezjański układ współrzędnych.
Opis ruchu w układzie odniesienia
- Wektor położenia
Wersory kierunków: [math] \begin{matrix} \vec{i} = (1,0,0)\\ \vec{j} = (0,1,0)\\ \vec{k} = (0,0,1) \end{matrix} [/math]
x, y, z — wartości współrzędnych
[math] \vec{r} = x\vec{i}+y\vec{j}+z\vec{k}[/math] - Droga — długość toru — wielkość skalarna (zwyczajowo oznaczana literą s)
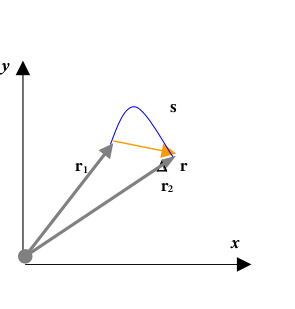
- Przesunięcie [math]\Delta \vec{r} = \vec{r}_2-\vec{r}_1[/math] Przesunięcie i droga to dwie zupełnie różne wielkości. Ich wielkości są sobie równe tylko w ruchu po prostej w bez zmiany kierunku.
- Prędkość chwilowa albo rzeczywista
[math] v_{ch} = \lim_{\Delta t \rightarrow 0} \frac{x(t+\Delta t)-x(t)}{\Delta t} =\frac{dx}{dt}[/math]
[math] \vec{v}_{ch} = \lim_{\Delta t \rightarrow 0} \frac{\vec{r}(t+\Delta t)-\vec{r}(t)}{\Delta t} =\frac{d\vec{r}}{dt}[/math] - Prędkość średnia
[math]v_{sr} = \frac{\Delta x}{\Delta t}[/math]
[math]\vec{v}_{sr} = \frac{\vec{x}_2(t_2)-\vec{x}_(t_1)}{t_2-t_2}[/math]
Definicja ogólna
[math]\vec{v}_{sr} = \frac{\Delta \vec{x}}{\Delta t}[/math] - Przyspieszenie
- Definicja dla ruchu prostoliniowego
[math] a_{x_{ch}} = \lim_{\Delta t\rightarrow 0} \frac{v_x(t+\Delta t)-v_x(t)}{\Delta t} = \frac{dv_x}{dt}[/math] - Definicja ogólna
[math]\vec{a}_{ch} = \lim_{\Delta t \rightarrow 0} \frac{\vec{v}(t+\Delta t)-\vec{v}(t)}{\Delta t}[/math]
- Definicja dla ruchu prostoliniowego
Analiza ruchu prostoliniowego jednostajnego i jednostajnie zmiennego w oparciu o doświadczenia i powiązanie informacji z matematyki o wykresach funkcji liniowej i kwadratowej. Analiza wykresów drogi i prędkości od czasu dla tych ruchów.
Przykład opisu ruchu
Ruch kajaka w kierunku prostopadłym do prądu rzeki
Zastanówmy się teraz, jak zapisać wektor położenia, by opisywał on ruch kajaka. Kajak się porusza, a więc składowe wektora muszą się również zmieniać Zależność wektora położenia od czasu [math]\vec{r}(t)[/math], wyrażona poprzez funkcje [math]x(t)[/math], [math]y(t)[/math], [math]z(t)[/math] nosi nazwę parametrycznego równania toru. Parametrem w tych równaniach jest czas.
Współrzędne poruszającego się kajaka w układzie związanym z brzegiem rzeki zapiszemy następująco:
[math]\left.
\begin{matrix}
x(t)= v_r t\\
y(t)= v_w t\\
z(t)= 0
\end{matrix}
\right\} \vec{r}(t)
[/math]
Jeśli z powyższych równań wyeliminuje się czas, to uzyska się zależność y(x). Będzie to równanie opisujące kształt toru na płaszczyźnie. W omawianym przykładzie, jeśli z pierwszego równania wyznaczymy czas t i wstawimy do drugiego równania, to uzyskamy:
[math] y(x) = \frac{v_w}{v_r} x[/math]
Jest to równanie prostej. Wszystko się zgadza! Kajak porusza się po prostej. Kąt, jaki tworzy prosta z brzegiem rzeki, zależy od stosunku prędkości — prędkości, którą nadajemy kajakowi i prędkości prądu rzeki. Taki stosunek, to tangens kąta nachylenia prostej do osi x. Przypomnijmy, że tangens kąta nachylenia prostej jest równy współczynnikowi kierunkowemu prostej.
Ruch po okręgu
Prędkość kątowa [math] \omega = \frac{d\alpha}{dt}[/math]
W ruchu jednostajnym [math] \alpha = \omega t[/math]
Parametryczne równanie toru: [math] x = r \cos\alpha[/math]
[math] y = r \sin\alpha[/math]
[math] x^2+y^2 = r^2[/math]
[math] v_x = -\omega r \sin \alpha[/math]
[math] v_y = \omega r \cos\alpha [/math]
Kierunek wektora styczny do toru.( pokaz i jego omówienie).