Fizyka I OO/Wykład IV

Pojęcia fizyczne i prawa fizyczne wprowadzone na wykładzie

• swobodny spadek w polu grawitacyjnym
• rzuty pionowe
• rzut poziomy
• siła tarcia

1. Swobodny spadek bez oporów ruchu ( rura próżniowa)
2. Rzut poziomy jako złożenie ruchu jednostajnego i jednostajnie zmiennego
3. Programy komputerowe symulujące rzuty, zdjęcia stroboskopowe.
4. Badanie siły tarcia: siłomierze, klocki, podłoże o różnym współczynniku tarcia

Dynamiczne skutki działania nie zrównoważonej siły

Swobodny spadek ciał

Gdy nie ma sił oporu ruchu przyspieszenie ruchu jest równe przyspieszeniu grawitacyjnemu. Przyspieszenie grawitacyjne nie zależy od masy ciała.
[math] y = h-\frac{gt^2}{2}[/math]

Rzut pionowy w dół

[math]y = h- gt -\frac{gt^2}{2}[/math]

Rzut pionowy w górę

[math]y = h+ gt -\frac{gt^2}{2}[/math]

Rzut poziomy

Parametryczne równanie toru
[math]\begin{matrix} x(t) = v_xt\\ y(t) = h-\frac{gt^2}{2} \end{matrix}[/math]
[math] y(x) = h-\frac{gx^2}{2v^2_x}[/math] — torem jest parabola
h — odległość od podłoża, [math]v_x[/math] — prędkość początkowa nadana w kierunku poziomym.

Siła tarcia

Cykl pokazów, z których wynika że:

• współczynnik tarcia statycznego jest większy od współczynnika tarcia posuwistego
• siła tarcia posuwistego zależy od siły nacisku i współczynnika

[math] T = Nf[/math]

[math] T= Nfs[/math]

Przykład 1

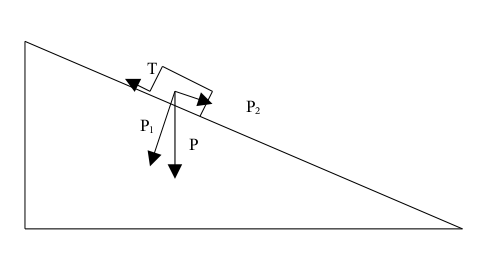
Oblicz przyspieszenie klocka zsuwającego się z równi pochyłej o kącie nachylenia [math]\alpha[/math] i współczynniku tarcia f.

Siłę ciężkości [math]\vec{P}[/math], jak każdy wektor, możesz rozłożyć na dwa dowolne wektory, byle wektor [math]\vec{P}[/math] był przekątną równoległoboku utworzonego na tych wektorach. Nas, oczywiście, nie będą interesowały wektory o dowolnych kierunkach. Wyróżnimy kierunek równoległy do powierzchni równi i kierunek prostopadły do powierzchni równi (rys. Figure 1). Wzdłuż tych dwóch kierunków rozłóżmy siłę [math]\vec{P}[/math]. Uzyskamy składowe [math]\vec{P}_1[/math] i [math]\vec{P}_2[/math] o wartościach [math]P_1 = P \cos \alpha[/math] i [math]P_2= P \sin \alpha[/math]. Siła [math]P_1[/math] zostanie zrównoważona przez siłę sprężystości powie­rzchni równi R, a siła [math]P_2[/math] pozostanie nie zrów­noważona i będzie powodowała ruch jednostajnie przyspieszony klocka.

Przyspieszenie klocka jest równe:

[math]a_1 = \frac{P\sin\alpha}{m} = \frac{mg\sin \alpha}{m} = g\sin\alpha[/math]

Obliczone przyspieszenie jest mniejsze od grawitacyjnego (sinus kąta nachylenia równi jest mniejszy od jedynki).

W tej części przykładu została zaniedbana siła tarcia. Jeśli ją uwzględnimy, to są dwie możliwości:

• Klocek pozostanie nieruchomy, jeśli siła zsuwająca i siła tarcia będą się równoważyć.
• Klocek będzie poruszał się z przyspieszeniem, ale mniejszym niż w poprzednim wypadku, ponieważ nie zrównoważoną siłą będzie wypadkowa siły zsuwającej [math]P_2[/math] i siły tarcia T.

[math]a = \frac{P_2-T}{m}[/math]

Obliczmy siłę tarcia. Jest ona równa sile nacisku pomnożonej przez współczynnik tarcia. Tym razem siła nacisku ma wartość składowej [math]P_1[/math]. A więc

[math]T=mgf\cos\alpha[/math]

Zatem przyspieszenie zsuwającego się klocka wyniesie

[math] a = g sin\alpha - gf \cos\alpha = g(sin\alpha - f\cos\alpha)[/math]

Przykład 2

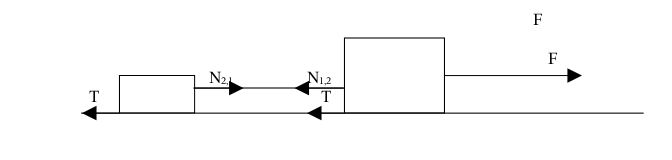
Dwa klocki o masach [math]m_1[/math] i [math]m_2[/math] połączone są linką. Do pierwszego z nich przyłożona jest siła [math]\vec{F}[/math] (rys. Figure 2). Z jakim przyspieszeniem porusza się układ, jeśli na każdy z klocków działa siła oporów ruchu [math]\vec{T}[/math]. Jaka jest siła napięcia linki [math]\vec{N}[/math]?

Rozwiązanie

Rozważmy siły działające na każdy klocek. Niech siła [math]\vec{F}_1[/math] oznacza wypadkową sił działających na pierwszy klocek, a [math]\vec{F}_2[/math] odpowiednio na drugi. Obliczając te siły pamiętamy, że o ruchu ciała decydują siły, które są przyłożone do tego ciała.

[math]\vec{N}_{12}= \vec{N}_{21} = \vec{N}[/math] &mdash wartość sił napięcia linki jest taka sama. Siły te różnią się punktem przyłożenia i dlatego ich oznakowanie na rysunku jest różne.

[math]\vec{F}_1 = \vec{F}+\vec{N} + \vec{T}[/math]	[math]\vec{F}_2 = \vec{N} + \vec{T}[/math]
[math]\vec{a}m_1 = \vec{F}-\vec{N} - \vec{T}[/math]	[math]\vec{a}m_2 = \vec{N} - \vec{T}[/math]

Po dodaniu stronami dwu ostatnich równań uzyskujemy: [math] a (m_1+m_2) - F-N+N -2T[/math]

[math] a = \frac{F-2T}{m_1+m_2}[/math]

Siłę napięcia linki znajdujemy następująco:

[math] N = a m_2 +T = \frac{F-2T}{m_1+m_2}m_2 +T[/math]