Funkcje
Funkcja
Funkcją (stosuje się też nazwę odwzorowanie) określoną na zbiorze [math]X\;[/math] o wartościach w zbiorze [math]Y\;[/math] nazywamy przyporządkowanie każdemu elementowi [math]x\in X\;[/math] dokładnie jednego elementu [math]y\in Y\;[/math]. [math]x\;[/math] nazywamy argumentem, zaś [math]y\;[/math] — wartością funkcji. Zbiór [math]X\;[/math] nazywamy dziedziną funkcji.
Zapisujemy: [math]y=f(x)\;[/math]. Dla jednoczesnego podania funkcji (sposobu przyporządkowania) oraz zbiorów [math]X\;[/math] i [math]Y\;[/math] piszemy: [math]f: X\to Y\;[/math].
Uwaga
Do definicji funkcji trzeba podać trzy rzeczy: [math]f\;[/math], [math]X\;[/math], [math]Y\;[/math]. Dwie funkcje: [math]f: X_1\to Y_1\;[/math] oraz [math]f: X_2 \to Y_2\;[/math], dla których sposób przyporządkowania [math]f\;[/math] jest taki sam, ale [math]X_1\ne X_2\;[/math] lub [math]Y_1\ne Y_2\;[/math], uważamy za różne! Np. [math]f: \mathbb R \to \mathbb R: f(x) =x+1 \;[/math] oraz [math]f: \mathbb N \to \mathbb N: f(x) = x+1\;[/math], uważamy za różne, mimo iż recepta przyporządkowania jest ta sama!
Injekcja
Injekcją nazywamy odwzorowanie o własności:
[math]\forall x_1,x_2 \in X \,:\,(f(x_1) = f(x_2)) \Longrightarrow (x_1 = x_2)\;.[/math]
(innymi słowy, jest to odwzorowanie różnowartościowe)
Surjekcja
Surjekcją nazywamy takie odwzorowanie, że każdy [math]y\in Y\;[/math] jest obrazem pewnego [math]x\in X\;[/math]. Zapiszmy to używając kwantyfikatorów: [math] \mathop{\forall}_{y\in Y} \mathop{\exists}_{x\in X}: y=f(x)\;[/math]. W tym przypadku mówimy też, że [math]f\;[/math] jest odwzorowaniem "na".
Bijekcja
Bijekcją nazywamy odwzorowanie, które jest jednocześnie injekcją i surjekcją.
Przykład
Rozważmy trzy funkcje [math]f_1, f_2, f_3\;[/math]: [math]f_1: \mathbb R\to\mathbb R, f_1(x):=x^2\;[/math]; [math]f_2: \mathbb R\to\mathbb R_+ \cup \{0\}, f_2(x):=x^2\;[/math]; [math]f_3: \mathbb R_+ \cup \{0\} \to\mathbb R_+ \cup \{0\} , f_3(x):=x^2\;[/math].
[math]f_1\;[/math] nie jest iniekcją ani surjekcją;
[math]f_2\;[/math] nie jest injekcją, ale jest surjekcją;
wreszcie [math]f_3\;[/math] jest zarówno injekcją jak i surjekcją.
Przykład ten pokazuje, w jak dużym (decydującym!) stopniu własności funkcji (injektywność, surjektywność itp.) zależą od zbioru, na którym są określone.
Odwzorowanie odwrotne
Bijekcje są ważną klasą odwzorowań, gdyż można dla nich określić odwzorowanie odwrotne:
Jeśli [math]f: X\to Y\;[/math] jest bijekcją, to odwzorowaniem odwrotnym do [math]f\;[/math] (oznaczanym jako [math]f^{-1})\;[/math] jest odwzorowanie [math]f^{-1}: Y\to X\;[/math], definiowane tak: Jeśli [math]y=f(x)\;[/math], to [math]f^{-1}(y)=x\;[/math].
Przykład
Weźmy [math]f_3\;[/math] z powyższego przykładu. Mamy tu [math]y=f(x)=x^2\;[/math], więc [math]x=+\sqrt{y}=f^{-1}(y)\;[/math].
Obraz
Obrazem zbioru [math]A\subset X\;[/math] przy odwzorowaniu [math]f\;[/math] nazywamy zbiór [math]B\subset Y\;[/math] oznaczany jako [math]B=f(A)\;[/math] i określony jako
Przeciwobraz
Przeciwobrazem zbioru [math]C\subset Y\;[/math] przy odwzorowaniu [math]f\;[/math] nazywamy zbiór [math]E\subset X\;[/math], oznaczany jako [math]E=f^{-1}(C)\;[/math] i określony jako
Przykład
Rozważmy funkcję [math]f_1\;[/math] z powyższego przykładu: [math]f_1: \mathbb R\to\mathbb R, f_1(x):=x^2\;[/math]. Mamy: [math]f_1([1,2])=[1,4]\;[/math], zaś [math]f^{-1}([1,4])=[1,2]\cup [-2,-1]\;[/math].
Poziomica
Poziomicą punktu [math]c\in Y\;[/math] nazywamy przeciwobraz punktu [math]c\in Y\;[/math].
Przykład
Rozważmy funkcję [math]g: \mathbb R^2 \to \mathbb R\;[/math], określoną jako: [math]g(x,y)=x^2+y^2\;[/math]. Wtedy, dla [math]c\gt 0\;[/math], poziomica to zbiór punktów płaszczyzny spełniających równanie: [math]x^2+y^2=c\;[/math], w czym rozpoznajemy równanie okręgu o promieniu [math]\sqrt{c}\;[/math]. Dla [math]c=0\;[/math] poziomicą jest punkt [math](0,0)\;[/math], a dla [math]c\lt 0\;[/math] — zbiór pusty.
Wykres funkcji
Jako że zmysłem człowieka, odbierającym zdecydowaną większość bodźców jest wzrok, nic dziwnego, że łatwiej dostrzeżemy różne aspekty funkcji patrząc na jej wykres.
Def. Wykresem funkcji [math]f:X\to Y\;[/math] nazywamy następujący podzbiór [math]G\;[/math] iloczynu kartezjańskiego [math] X\times Y \;[/math]: [math]G=\{(x,f(x))\in X\times Y\}\;[/math].
W sytuacjach, z którymi teraz będziemy mieć do czynienia (tzn. wykresami funkcji rzeczywistych o argumentach rzeczywistych), wykres jest podzbiorem płaszczyzny, tzn. zbiorem par [math](x,y)\;[/math]. Na osi poziomej zaznaczamy argumenty [math]x\;[/math], a na osi pionowej wartości funkcji [math]y=f(x)\;[/math].
Miejsce zerowe
Miejscem zerowym [math]x_0\;[/math] funkcji [math]f\;[/math] nazywamy argument taki, że [math]f(x_0)\;[/math]=0.
Używając dopiero co wprowadzonej terminologii mówimy, że zbiorem miejsc zerowych funkcji [math]f\;[/math] jest poziomica:[math]f^{-1}(0)\;[/math].
Własności funkcji
Następujące właściwości funkcji rzeczywistych (tzn. [math]f:X\to Y\;[/math], gdzie [math]X,Y\;[/math] są podzbiorami [math]\mathbb R\;[/math]) są często ważne w zastosowaniach.
Monotoniczność funkcji
- Funkcję [math]f:X\to Y\;[/math] nazywamy rosnącą na zbiorze [math]A\subset X\;[/math] [math]\Longleftrightarrow \mathop{\forall}{x_1,x_2\in A}:x_1\lt x_2 \Longrightarrow f(x_1)\lt f(x_2)\;[/math]
- Funkcję [math]f:X\to Y\;[/math] nazywamy malejącą na zbiorze [math]A\subset X\;[/math] [math]\Longleftrightarrow \mathop{\forall}{x_1,x_2\in A}:x_1\lt x_2 \Longrightarrow f(x_1)\gt f(x_2)\;[/math]
- Funkcję [math]f:X\to Y\;[/math] nazywamy stałą na zbiorze [math]A\subset X\;[/math] [math]\Longleftrightarrow \mathop{\forall}{x_1,x_2\in A}: f(x_1)=f(x_2)\;[/math]
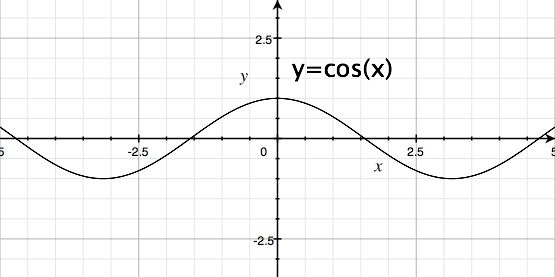
Parzystość
Funkcję [math]f:X\to Y\;[/math] nazywamy parzystą [math]\Longleftrightarrow \mathop{\forall}{x\in D}: f(x)=f(-x)\;[/math].
Wykres funkcji parzystej jest symetryczny względem osi [math]OY\;[/math].
Przykład
Funkcja [math]cos(x)\;[/math] jest parzysta na [math]\mathbb R.\;[/math]
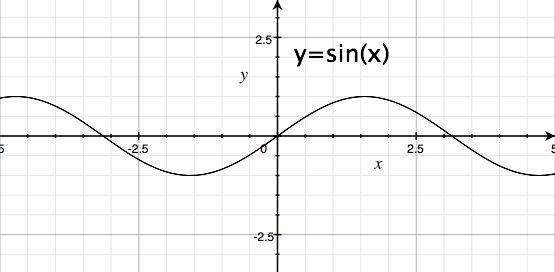
Nieparzystość
Funkcję [math]f:X\to Y\;[/math] nazywamy nieparzystą [math]\Longleftrightarrow \mathop{\forall}{x\in D}: f(x)=-f(-x)\;[/math].
Wykres funkcji parzystej jest symetryczny względem punktu [math](0,0)\;[/math].
Przykład
Funkcja [math]sin(x)\;[/math] jest nie parzysta na [math]\mathbb R.\;[/math]
Ograniczenie z dołu
Funkcję [math]f\;[/math] nazywamy ograniczoną z dołu[math]\Longleftrightarrow \exists_{m \in \mathbb R}:\forall_{x\in D}: f(x)\geq m \;[/math]
Ograniczenie z góry
Funkcję [math]f\;[/math] nazywamy ograniczoną z góry[math]\Longleftrightarrow \exists_{M \in \mathbb R}:\forall_{x\in D}: f(x)\leq M \;[/math]
Ograniczenie
Funkcję [math]f\;[/math] nazywamy ograniczoną jeśli jest jednocześnie ograniczona z góry i z dołu.
Przykład
Funkcja [math]F_1: \mathbb R_+\ni x \to F_1(x):=\frac{1}{x}\in \mathbb R\;[/math] jest ograniczona z dołu; [math]F_2: \mathbb R_-\ni x \to F_2(x):=\frac{1}{x}\in \mathbb R\;[/math] jest ograniczona z góry; [math]F_3: \mathbb R\setminus \{0\} \ni x \to F_3(x):=\frac{1}{x}\in \mathbb R\;[/math] nie jest ograniczona; a funkcja [math]F_4: \mathbb R \ni x \to F_4(x):=sin^2(x)\in \mathbb R\;[/math] jest ograniczona.
Największa wartość
Funkcja [math]f:X\to Y\;[/math] przyjmuje największą wartość [math]y_{max}\in Y\;[/math] dla [math]x_0\in X \Longleftrightarrow f(x_0)=y_{max}\;[/math] oraz [math]\forall_{x\in X}: f(x)\leq f(x_0)\;[/math].
Najmniejsza wartość
Analogicznie:
Def. Funkcja [math]f:X\to Y\;[/math] przyjmuje najmniejszą wartość [math]y_{min}\in Y\;[/math] dla [math]x_0\in X \Longleftrightarrow f(x_0)=y_{min}\;[/math] oraz [math]\forall_{x\in X}: f(x)\geq f(x_0)\;[/math].
Przekształcenia wykresu funkcji
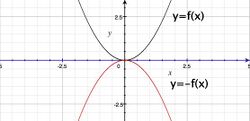
- Symetria względem osi [math]OX\;[/math]: Przekształcając wykres funkcji [math]y=f(x)\;[/math] przez symetrię względem osi [math]OX\;[/math], otrzymamy wykres funkcji [math]y=-f(x)\;[/math].
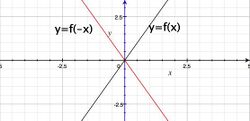
- Symetria względem osi [math]OY\;[/math]: Przekształcając wykres funkcji [math]y=f(x)\;[/math] przez symetrię względem osi [math]OY\;[/math], otrzymamy wykres funkcji [math]y=f(-x)\;[/math].
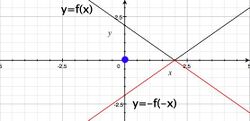
- Symetria względem punktu [math](0,0)\;[/math]: Przekształcając wykres funkcji [math]y=f(x)\;[/math] przez symetrię względem punktu [math](0,0)\;[/math], otrzymamy wykres funkcji [math]y=-f(-x)\;[/math].
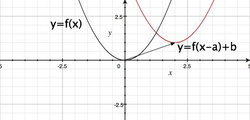
- Przesunięcie równoległe wykresu o wektor [math][a,b]\;[/math]: W wyniku przesunięcia równoległego wykresu funkcji [math]y=f(x)\;[/math] o wektor [math][a,b]\;[/math] otrzymujemy wykres funkcji [math]y=f(x-a)+b\;[/math].
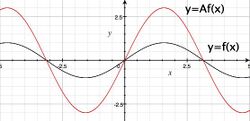
- Skalowanie wykresu funkcji: wykresy [math]y=f(x)\;[/math] oraz [math]y=A\;[/math]·[math]f(x)\;[/math].
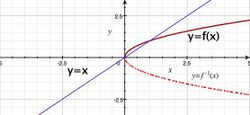
- Symetria względem prostej [math]y=x\;[/math]: Przekształcając w ten sposób wykres funkcji [math]y=f(x)\;[/math] otrzymamy wykres funkcji odwrotnej [math]y=f^{-1}(x)\;[/math].
Przykłady funkcji
Funkcja liniowa
Funkcją liniową nazywamy funkcję [math]f:\mathbb R\to\mathbb R\;[/math] określoną wzorem [math]f(x)=ax+b \,\;[/math], gdzie [math]a,b\in \mathbb R\;[/math].
Wykres
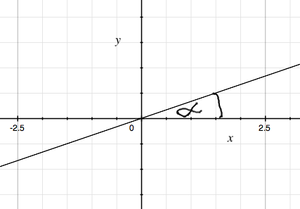
Wykresem funkcji liniowej [math]f(x)=ax+b \,\;[/math] jest prosta o równaniu [math]y=ax+b \,\;[/math], nachylona do osi [math]OX\;[/math] pod kątem [math]\alpha\;[/math] takim, że [math]a=tg\alpha\;[/math].
Monotoniczność
Funkcja liniowa jest:
- rosnąca [math]\Longleftrightarrow a\gt 0\;[/math],
- malejąca [math]\Longleftrightarrow a\lt 0\;[/math],
- stała [math]\Longleftrightarrow a=0\;[/math].
Jak uwzględnić proste pionowe
Jak powiedziano, wykresem funkcji liniowej jest prosta. Patrząc na wszystkie możliwe proste na płaszczyźnie, widzimy, że postać [math]y=ax+b\;[/math] obejmuje prawie wszystkie przypadki, z wyjątkiem jednej klasy — prostych pionowych. Aby uwzględnić także tę sytuację, dogodnie jest przyjąć ogólniejszą postać równań prostej, a mianowicie:
Warunki równoległości wykresów funkcji liniowych
- Proste zadane jako wykresy funkcji: [math]y=a_1 x + b_1 \,\;[/math] oraz [math]y=a_2 x + b_2 \,\;[/math] są równoległe [math]\Longleftrightarrow a_1=a_2\;[/math].
- Proste zadane w postaci ogólnej [math]A_1 x + B_1 y + C_1=0 \,\;[/math] oraz [math]A_2 x + B_2 y + C_2=0 \,\;[/math] są równoległe [math]\Longleftrightarrow A_1 B_2 - A_2 B_1=0\;[/math].
Równanie liniowe z jedną niewiadomą
Równaniem liniowym z jedną niewiadomą nazywamy równanie postaci [math]ax+b=0\;[/math], gdzie [math]a,b\in\mathbb R\;[/math].
Mogą zachodzić następujące sytuacje dotyczące rozwiązalności takiego równania:
- Jeśli [math]a\ne 0\;[/math], to równanie ma dokładnie jedno rozwiązanie [math]x=-\frac{b}{a}\;[/math].
- Jeśli [math]a=0\;[/math] i [math]b=0\;[/math], to rozwiązaniem równania jest dowolna liczba rzeczywista.
- Jeśli [math]a=0\;[/math] i [math]b\ne 0\;[/math], to równanie nie posiada rozwiązań
Układ dwu równań liniowych z dwiema niewiadomymi
Niech będzie dany układ dwu równań liniowych z dwiema niewiadomymi [math]x,y\;[/math]: [math] \left\{\begin{array}{ccccc} a_1 x & + & b_1 y & = & c_1\\ a_2 x & + & b_2 y & = & c_2 \end{array} \right.\; [/math]
- [math] W=\;\left|\begin{array}{cc}a_1 & b_1\\a_2 & b_2\end{array}\right|=a_1b_2-a_2b_1\;[/math];
- [math]W_x=\left|\begin{array}{cc}c_1 & b_1\\c_2 & b_2\end{array}\right|=c_1b_2-c_2b_1\;[/math];
- [math]W_y=\left|\begin{array}{cc}a_1 & c_1\\a_2 & c_2\end{array}\right|=a_1 c_2 - c_2 b_1\;[/math];
Mogą zachodzić następujące sytuacje dotyczące rozwiązalności układu (1):
- Jeśli [math]W\ne 0\;[/math], to układ ma dokładnie jedno rozwiązanie: [math]x=-\frac{W_x}{W}\;[/math], [math]y=-\frac{W_y}{W}\;[/math]. Układ taki nazywamy układem oznaczonym.
- Jeśli [math]W=0=W_x=W_y\;[/math], to układ (1) posiada nieskończenie wiele rozwiązań; rozwiązaniem jest każda para liczb [math]x,y\;[/math] spełniająca dowolne równanie danego układu. Układ taki nazywamy układem nieoznaczonym.
- Jeśli [math]W=0\;[/math] i co najmniej jeden z wyznaczników [math]W_x, W_y\;[/math] jest różny od zera, to układ nie posiada rozwiązań. Układ taki nazywamy układem sprzecznym.
Funkcja kwadratowa
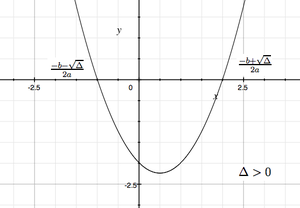
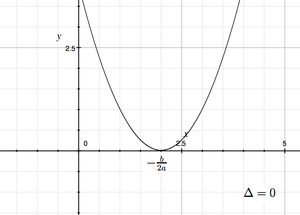
Funkcją kwadratową (trójmianem kwadratowym) nazywamy funkcję: [math]f(x)=ax^2+bx+c\;[/math], gdzie [math]a,b,c\in \mathbb R\;[/math], [math]a\ne 0\;[/math], [math]x\in \mathbb R\;[/math]. Wykresem funkcji kwadratowej [math]f(x) = ax^2+bx+c\;[/math] jest parabola o wierzchołku w punkcie [math]p=(-\frac{b}{2a},-\frac{\Delta}{4a})\;[/math], gdzie [math]\Delta:=b^2-4ac\;[/math] nazywamy wyróżnikiem trójmianu kwadratowego.
Miejsca zerowe funkcji kwadratowej
Funkcja kwadratowa [math]f(x) = ax^2+bx+c\;[/math]:
- ma dwa różne miejsca zerowe (pierwiastki):
[math]x_1=\frac{-b-\sqrt{\Delta}}{2a}\;[/math], [math]x_2=\frac{-b+\sqrt{\Delta}}{2a}\;[/math], gdy
- [math]\Delta\gt 0\;[/math];
- ma jedno miejsce zerowe [math]x_0=-\frac{b}{2a}\;[/math], gdy
- [math]\Delta=0\;[/math];
- nie ma miejsc zerowych, gdy
- [math]\Delta\lt 0\;[/math].
Przykład — rzut pionowy
Z miejsca znajdującego się 2 m nad podłogą rzucamy w górę piłkę z prędkością początkową 3 m⁄s. Po jakim czasie piłka upadnie na podłogę? Założyć wartość przyspieszenia ziemskiego 10 m⁄[math]s^2\;[/math].
Rozwiązanie
Droga w ruchu jednostajnie przyspieszonym określona jest wzorem: s(t)= a[math]t^2\;[/math]⁄2 + [math]v_0 t + s_0\;[/math], gdzie [math]a\;[/math] — przyspieszenie, [math]v_0\;[/math] — prędkość początkowa, [math]s_0\;[/math] — droga w chwili [math]t=0\;[/math]. Pytamy zatem, jakiej chwili czasu [math]t_0\;[/math] będzie odpowiadała wysokość [math]s(t_0)=0\;[/math].
Mamy więc równanie:
skąd: [math]\Delta= 49,\;\; \sqrt{\Delta}=7,\;\; t_1= 1 [s],\;\; t_2 = -0.4 [s]\;[/math]. Piłka upadnie na podłogę po upływie 1 sekundy. (Czemu odpowiada drugi pierwiastek [math]t_2\;[/math]?)
Pożyteczne są:
Postaci funkcji kwadratowej
- Postać kanoniczna: [math]y=a(x-p)^2+q\;[/math], gdzie [math]p=-\frac{b}{2a}\;[/math], [math]q=-\frac{\Delta}{4a}\;[/math].
- Postać iloczynowa: Istnieje [math]\Longleftrightarrow \Delta \geq 0\;[/math]. Jeśli tak jest, to:
- [math] y=a(x-x_0)^2\;[/math] gdy [math]\Delta=0\;[/math],
- [math] y=a(x-x_1)(x-x_2)\;[/math] gdy [math]\Delta\gt 0\;[/math].
Wzory Viète'a
Gdy równanie kwadratowe [math]ax^2+bx+c=0\;[/math] ma pierwiastki [math]x_1, x_2\;[/math], to zachodzą wzory Viète'a
Funkcje wymierne — homografie
Funkcję postaci: [math]f(x)=\frac{ax+b}{cx+d}\;[/math], gdzie [math]c\ne 0\;[/math] oraz [math]ad-bc\ne 0\;[/math], nazywamy homografią. Dziedziną homografii jest [math]\mathbb R\setminus \left \{ -\frac{d}{c} \right \}.[/math]
Wykresem funkcji homograficznej jest hiperbola: wykres funkcji [math]y=\frac{1}{x}\;[/math] odpowiednio poprzesuwany: Napiszmy równanie funkcji homograficznej:
Widać, iż ogólną homografię [math]f(x)=\frac{ax+b}{cx+d}\;[/math] powstaje ze "standardowej" [math]y=\frac{1}{x}\;[/math] przez:
- przesunięcie poziome o [math]x_0=-\frac{d}{c}\;[/math];
- przeskalowanie o czynnik [math]\frac{bc-ad}{c^2}\;[/math];
- przesunięcie pionowe o [math]y_0=\frac{a}{c}\;[/math].
Asymptoty
Prostą (poziomą) o równaniu [math]y=\frac{a}{c}\;[/math] nazywamy asymptotą poziomą; prostą (pionową) o równaniu [math]x=-\frac{d}{c}\;[/math] nazywamy asymptotą pionową.