Matematyka 1NI/Badanie funkcji

Z Brain-wiki

Badanie funkcji

Zadanie 1

Zbadać przebieg zmienności funkcji:

[math] f(x)=\frac{(x+1)(x-2)^2}{x^2+2} \, [/math]


Wskazówka

Należy zbadać kolejno następujące elementy: dziedzina, granice, asymptoty, punkty przecięcia wykresu z osiami współrzędnych, własności szczególne, pochodna, przedziały monotoniczności funkcji, ekstrema, druga pochodna, wklęsłość, wypukłość, a następnie sporządzić wykres funkcji.

Rozwiązanie

Badanie funkcji będziemy wykonywać w sposób systematyczny trzymając się podanych niżej punktów.

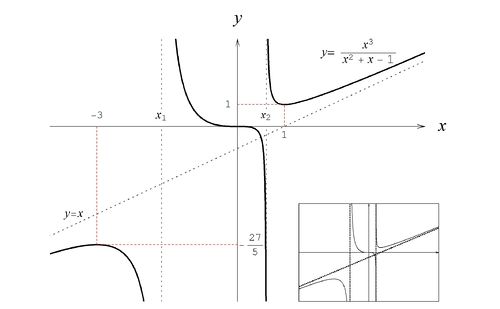
  1. Dziedzina funkcji. Wyrażenie (1) jest dobrze określone wszędzie, więc przyjmujemy [math]D=\mathbb{R}\, [/math].
  2. Własności szczególne. Badana funkcja nie jest ani okresowa, ani nie przekształca się prosto przy zamianie [math]x\longmapsto -x\, [/math].
  3. Granice na końcach przedziałów określoności. Musimy rozważyć jedynie granice przy [math]x\rightarrow \pm \infty \, [/math]. Wielomian w liczniku (1) ma wyższy stopień niż ten w mianowniku, więc łatwo otrzymujemy:
    [math] \lim_{x\rightarrow\infty}f(x)= \infty\; , \;\;\;\;\;\;\;\;\;\; \lim_{x\rightarrow -\infty}f(x)=-\infty\; . \, [/math]
  4. Asymptoty. Współczynnik kierunkowy asymptoty w [math]+\infty\, [/math] (o ile ona istnieje) oznaczymy symbolem [math]a_1\, [/math], a wyraz wolny [math]b_1\, [/math]. Parametry te znajdziemy, obliczając kolejno granice:
    [math] \lim_{x\rightarrow\infty}\frac{f(x)}{x}=1=:a_1 \, [/math]

    oraz

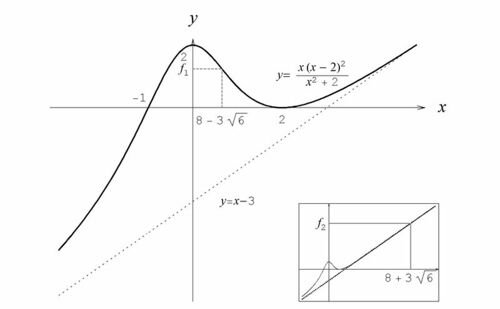
    [math] \lim_{x\rightarrow\infty} (f(x)-a_1 x)=-3=:b_1\; . \, [/math]

    Równanie prawej asymptoty ma więc postać: [math]y=x-3\, [/math]. Parametry lewej asymptoty oznaczymy odpowiednio [math]a_2\, [/math] i [math]b_2\, [/math]. Znajdziemy je obliczając najpierw:

    [math] \lim_{x\rightarrow-\infty}\frac{f(x)}{x}=1=:a_2\; , \, [/math]

    a następnie:

    [math] \lim_{x\rightarrow-\infty} (f(x)-a_2 x)=-3=:b_2\; . \, [/math]
    Równanie lewej asymptoty jest więc identyczne: [math]y=x-3\, [/math].
  5. Punkty przecięcia z osiami współrzędnych. Miejscami zerowymi funkcji są [math]x_1=-1\, [/math] oraz [math]x_2=2\, [/math], a punkt przecięcia z osią [math]y\, [/math] ma współrzędne [math](0,2)\, [/math].
  6. Pochodna funkcji. Obliczamy pochodną funkcji [math]f\, [/math]:
    [math] f'(x)=\frac{x(x^3+6x-20)}{(x^2+2)^2}\; . \, [/math]
    Pochodna istnieje wszędzie, gdzie określona jest sama funkcja (czyli [math]D'=\mathbb{R}\, [/math]).
  7. Przedziały monotoniczności i ekstrema funkcji. Mianownik wyrażenia (7) jest zawsze dodatni, więc można go pominąć przy badaniu znaków pochodnej, natomiast licznik można zapisać w formie:
    [math] x(x^3+6x-20)=x(x-2)(x^2+2x+10)\; . \, [/math]

    Ponieważ trójmian kwadratowy w nawiasie jest nierozkładalny, więc łatwo możemy stwierdzić, że:

    1. dla [math]x\in ]-\infty,0[\,[/math] zachodzi [math]f'(x)\gt 0\;\; \Longrightarrow\;\,[/math] funkcja jest rosnąca,
    2. dla [math]x\in ]0,2[\,[/math] zachodzi [math]f'(x)\lt 0\;\; \Longrightarrow\;\,[/math] funkcja jest malejąca,
    3. dla [math]x\in ]2,\infty[\,[/math] zachodzi [math]f'(x)\gt 0\;\; \Longrightarrow\;\,[/math] funkcja jest rosnąca.
    Ponadto [math]f'(x)=0\, [/math] dla [math]x=0\, [/math] oraz dla [math]x=2\, [/math]. Z otrzymanych rezultatów wynika, że w punkcie [math]x=0\, [/math] funkcja ma maksimum, przy czym [math]f(0)=2\, [/math], a w punkcie [math]x=2\, [/math] minimum, przy czym [math]f(2)=0\, [/math].
  8. Druga pochodna. Obliczamy teraz drugą pochodną:
    [math] f''(x)=-4\,\frac{x^3-15x^2-6x+10}{(x^2+2)^3}\; . \, [/math]
    Druga pochodna istnieje wszędzie, więc mamy [math]D''=\mathbb{R}\, [/math].
  9. Wypukłość, wklęsłość, punkty przegięcia. Wielomian w liczniku (9) można zapisać w formie:
    [math] x^3-15x^2-6x+10=(x+1)(x-8+3\sqrt{6})(x-8-3\sqrt{6})\; , \, [/math]

    Natomiast mianownik jest zawsze dodatni. Wynika stąd, że:

    1. dla [math]x\in ]-\infty,-1[\,[/math] zachodzi [math]f''(x)\gt 0\;\; \Longrightarrow\;\,[/math] funkcja jest wypukła,
    2. dla [math]x\in ]-1, 8-3\sqrt{6}[\,[/math] zachodzi [math]f''(x)\lt 0\;\; \Longrightarrow\;\,[/math] funkcja jest wklęsła,
    3. dla [math]x\in ]8-3\sqrt{6},8+3\sqrt{6}[\,[/math] zachodzi [math]f''(x)\gt 0\;\; \Longrightarrow\;\,[/math] funkcja jest wypukła,
    4. dla [math]x\in ]8+3\sqrt{6},\infty[\,[/math] zachodzi [math]f''(x)\lt 0\;\; \Longrightarrow\;\,[/math] funkcja jest wklęsła.
    W punktach [math]-1\, [/math], [math]8-3\sqrt{6}\, [/math] oraz [math]8+3\sqrt{6}\, [/math] funkcja ma punkty przegięcia, przy czym [math]f(-1)=0\, [/math], [math]f(8-3\sqrt{6})=:f_1\approx 1.24\, [/math], a [math]f(8+3\sqrt{6})=:f_2\approx 12.26\, [/math].

Teraz wszystkie otrzymane informacje zbierzemy w formie tabeli:

[math]x\,[/math] [math]-\infty \,\nearrow[/math] [math]-1\,[/math] [math]0\,[/math] [math]8-3\sqrt{6}\,[/math] [math]2\,[/math] [math]8+3\sqrt{6}\,[/math] [math]\infty\,[/math]
[math]f(x)\,[/math] [math]-\infty \,[/math] [math]\nearrow \,[/math] [math]0\,[/math] [math]\nearrow \,[/math] [math]2\,[/math] [math]\searrow \,[/math] [math]f_1\,[/math] [math]\searrow \,[/math] [math]0\,[/math] [math]\nearrow \,[/math] [math]f_2\,[/math] [math]\nearrow \,[/math] [math]\infty \,[/math]
[math]f'(x)\,[/math] [math]+++\,[/math] [math]+\,[/math] [math]+\,[/math] [math]0\,[/math] [math]-\,[/math] [math]-\,[/math] [math]-\,[/math] [math]0\,[/math] [math]+\,[/math] [math]+\,[/math] [math]+++\,[/math]
[math]f''(x)\,[/math] [math]+++\,[/math] [math]0\,[/math] [math]-\, [/math] [math]-\,[/math] [math]-\,[/math] [math]0\,[/math] [math]+\,[/math] [math]+\,[/math] [math]+\, [/math] [math]0\,[/math] [math]---\,[/math]

Na jej podstawie można już łatwo sporządzić wykres funkcji, który przedstawiony jest na rysunku Figure 1.


Wykres funkcji (1). Należy zwrócić uwagę, że gdy [math]x\rightarrow\infty\, [/math], wykres przecina asymptotę i przybliża się do niej od dołu, gdyż w punkcie [math]8+3\sqrt{6}\approx 15.35\, [/math] funkcja ma punkt przegięcia, który trudno jest uwidocznić na rysunku.

Zadanie 2

Zbadać przebieg zmienności funkcji:

[math] f(x)=\frac{x^3}{x^2+x-1} \, [/math]


Wskazówka

Należy zbadać kolejno następujące elementy: dziedzina, granice, asymptoty, punkty przecięcia wykresu z osiami współrzędnych, własności szczególne, pochodna, przedziały monotoniczności funkcji, ekstrema, druga pochodna, wklęsłość, wypukłość, a następnie sporządzić wykres funkcji.

Rozwiązanie

Podobnie jak w poprzednim zadaniu, badanie funkcji prowadzić będziemy w sposób systematyczny, trzymając się wypracowanej metody.

  1. Dziedzina funkcji. Wyrażenie (11) nie jest dobrze określone tam, gdzie są zera mianownika, a zatem w punktach:

    [math]\displaystyle x_1=-\frac{1}{2}- \frac{1}{2}\,\sqrt{5}\;\;\;\; \mathrm{oraz}\;\;\;\; x_2=-\frac{1}{2}+ \frac{1}{2}\,\sqrt{5}\; . [/math]

    Mamy więc [math]\displaystyle D=\mathbb{R}\setminus\{-\frac{1}{2}- \frac{1}{2}\,\sqrt{5}, -\frac{1}{2}+ \frac{1}{2}\,\sqrt{5}\}\, [/math].
  2. Własności szczególne. Badana funkcja nie jest ani okresowa, ani nie przekształca się prosto przy zamianie: [math]x\longmapsto -x\, [/math].
  3. Granice na końcach przedziałów określoności. Obliczamy po kolei:
    [math] \begin{array}{ccl} \lim_{x\rightarrow-\infty}f(x)&\!\!\! =&\!\!\! -\infty\; , \\ \lim_{x\rightarrow x_1^-}f(x)&\!\!\! =&\!\!\! -\infty\; , \\ \lim_{x\rightarrow x_1^+}f(x)&\!\!\! =&\!\!\! \infty\; ,\\ \lim_{x\rightarrow x_2^-}f(x)&\!\!\! =&\!\!\! -\infty\; , \\ \lim_{x\rightarrow x_2^+}f(x)&\!\!\! =&\!\!\! \infty\; , \\ \lim_{x\rightarrow\infty}f(x)&\!\!\! =&\!\!\! \infty\; . \end{array}\, [/math]
  4. Asymptoty. Z otrzymanych powyżej granic wynika, że proste [math]x=x_1\, [/math] i [math]x=x_2\, [/math] są asymptotami pionowymi dla wykresu funkcji. Pozostaje jeszcze zbadać ewentualne asymptoty ukośne przy [math]x\rightarrow \pm\infty\, [/math]. Stosując oznaczenia identyczne jak w poprzednim zadaniu, obliczamy:
    [math] \lim_{x\rightarrow\infty}\frac{f(x)}{x}=1=:a_1 \, [/math]

    oraz

    [math] \lim_{x\rightarrow\infty} (f(x)-a_1 x)=-1=:b_1\; . \, [/math]

    Równanie prawej asymptoty ma więc postać: [math]y=x-1\, [/math]. Dla lewej asymptoty uzyskujemy:

    [math] \lim_{x\rightarrow-\infty}\frac{f(x)}{x}=1=:a_2\; , \, [/math]

    a następnie:

    [math] \lim_{x\rightarrow-\infty} (f(x)-a_2 x)=-1=:b_2\; . \, [/math]
    Równanie lewej asymptoty jest więc identyczne: [math]y=x-1\, [/math].
  5. Punkty przecięcia z osiami współrzędnych. Jedynym miejscem zerowym funkcji jest [math]x_0=0\, [/math] i jest to zarazem punkt przecięcia wykresu z osią [math]y\, [/math].
  6. Pochodna funkcji. Obliczamy pochodną funkcji [math]f\, [/math]:
    [math] f'(x)=\frac{x^2(x^2+2x-3)}{(x^2+x-1)^2}\; . \, [/math]
    Pochodna istnieje wszędzie, gdzie określona jest sama funkcja (czyli [math]\displaystyle D'=\mathbb{R}\setminus\{-\frac{1}{2}- \frac{1}{2}\,\sqrt{5}, -\frac{1}{2}+ \frac{1}{2}\,\sqrt{5}\}\, [/math]).
  7. Przedziały monotoniczności i ekstrema funkcji. Mianownik wyrażenia (17) jest nieujemny, więc można go pominąć przy badaniu znaków pochodnej, natomiast licznik można zapisać w formie:
    [math] x^2(x^2+2x-3)=x^2(x-1)(x+3)\; . \, [/math]

    Na tej podstawie łatwo możemy stwierdzić, że:

    1. dla [math]x\in ]-\infty,-3[\,[/math] zachodzi [math]f'(x)\gt 0\;\; \Longrightarrow\;\,[/math] funkcja jest rosnąca,
    2. dla [math]x\in ]-3, x_1[\,[/math] zachodzi [math]f'(x)\lt 0\;\; \Longrightarrow\;\,[/math] funkcja jest malejąca,
    3. dla [math]x\in ]x_1,x_2[\,[/math] zachodzi [math]f'(x)\leq 0\;\; \Longrightarrow\;\,[/math] funkcja jest malejąca.
    4. dla [math]x\in ]x_2,1[\,[/math] zachodzi [math]f'(x)\lt 0\;\; \Longrightarrow\;\,[/math] funkcja jest malejąca,
    5. dla [math]x\in ]1,\infty[\,[/math] zachodzi [math]f'(x)\gt 0\;\; \Longrightarrow\;\,[/math] funkcja jest rosnąca.
    Ponadto [math]f'(x)=0\, [/math] dla [math]x=-3\, [/math], [math]x=0\, [/math] oraz dla [math]x=1\, [/math]. Z otrzymanych rezultatów wynika, że w punkcie [math]x=-3\, [/math] funkcja ma maksimum, przy czym [math]\displaystyle f(-3)=-\frac{27}{5}\, [/math], w punkcie [math]x=1\, [/math] minimum, przy czym [math]f(1)=1\, [/math]. W punkcie [math]x=0\, [/math] funkcja ma punkt przegięcia.
  8. Druga pochodna. Obliczamy teraz drugą pochodną:
    [math] f''(x)=2\,\frac{x(2x^2-3x+3)}{(x^2+x-1)^3}\; . \, [/math]
    Druga pochodna istnieje wszędzie, gdzie określona jest funkcja [math]f\, [/math], więc mamy [math]\displaystyle D''=\mathbb{R}\setminus\{-\frac{1}{2}- \frac{1}{2}\,\sqrt{5}, -\frac{1}{2}+ \frac{1}{2}\,\sqrt{5}\}\, [/math].
  9. Wypukłość, wklęsłość, punkty przegięcia. Analizując znak wyrażenia (19) dochodzimy do wniosku, że:
    1. dla [math]x\in ]-\infty,x_1[\,[/math] zachodzi [math]f''(x)\lt 0\;\; \Longrightarrow\;\,[/math] funkcja jest wklęsła,
    2. dla [math]x\in ]x_1, 0[\,[/math] zachodzi [math]f''(x)\gt 0\;\; \Longrightarrow\;\,[/math] funkcja jest wypukła,
    3. dla [math]x\in ]0,x_2[\,[/math] zachodzi [math]f''(x)\lt 0\;\; \Longrightarrow\;\,[/math] funkcja jest wklęsła,
    4. dla [math]x\in ]x_2,\infty[\,[/math] zachodzi [math]f''(x)\gt 0\;\; \Longrightarrow\;\,[/math] funkcja jest wypukła.
    Wyniki te potwierdzają, że dla [math]x=0\, [/math] funkcja ma punkt przegięcia.

Teraz wszystkie otrzymane informacje zbierzemy w formie tabeli.

[math]x\, [/math] [math]-\infty \,[/math] [math]-3\, [/math] [math]x_1\, [/math] [math]0\, [/math] [math]x_2\, [/math] [math]1\, [/math] [math]\infty\, [/math]
[math]f(x)\, [/math] [math]-\infty \, [/math] [math]-\frac{27}{5}\, [/math] [math]\searrow \, [/math] [math]\times\, [/math] [math]\infty\, [/math] [math]\searrow \, [/math] [math]0\,[/math] [math]\searrow \,[/math] [math]\times\, [/math] [math]\infty\, [/math] [math]1\, [/math] [math]\nearrow \, [/math] [math]\infty \, [/math]
[math]f'(x)\, [/math] [math]+++\, [/math] [math]0\, [/math] [math]---\, [/math] [math]\times\, [/math] [math]---\, [/math] [math]0\, [/math] [math]---\, [/math] [math]\times\, [/math] [math]---\, [/math] [math]0\, [/math] [math]+++\, [/math]
[math]f''(x)\, [/math] [math]---\, [/math] [math]-\, [/math] [math]---\, [/math] [math]\times\, [/math] [math]+++\, [/math] [math]0\, [/math] [math]---\, [/math] [math]\times\, [/math] [math]+++\, [/math] [math]+\, [/math] [math]+++\, [/math]


Na jej podstawie można już łatwo sporządzić wykres funkcji, który przedstawiony jest na rysunku %i 2.

Wykres funkcji (11).


Zadanie 3

Zbadać przebieg zmienności funkcji:

[math] f(x)=\frac{9x}{x^2+1}+x \, [/math]


Wskazówka

Należy zbadać kolejno następujące elementy: dziedzina, granice, asymptoty, punkty przecięcia wykresu z osiami współrzędnych, własności szczególne, pochodna, przedziały monotoniczności funkcji, ekstrema, druga pochodna, wklęsłość, wypukłość, a następnie sporządzić wykres funkcji.

Rozwiązanie
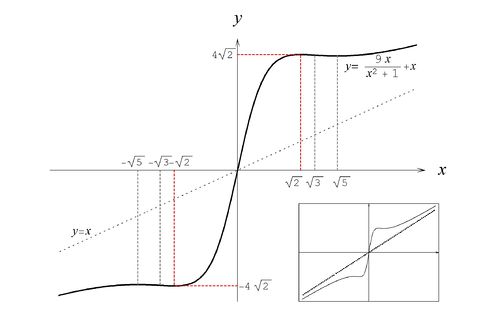
  1. Dziedzina funkcji. Funkcja (20) jest wszędzie dobrze określona, więc mamy: [math]D=\mathbb{R}\, [/math].
  2. Własności szczególne. Zachodzi: [math]f(-x)=-f(x)\, [/math], więc badana funkcja jest nieparzysta.
  3. Granice na końcach przedziałów określoności. Mamy do znalezienia jedynie granice funkcji w nieskończonościach. Ponieważ pierwszy wyraz zbiega wtedy do zera, więc łatwo otrzymujemy:
    [math] \lim_{x\rightarrow\infty}f(x)= \infty\; , \;\;\;\;\;\;\;\;\;\; \lim_{x\rightarrow -\infty}f(x)=-\infty\; . \, [/math]
  4. Asymptoty. Zbadamy istnienie ewentualnych asymptot ukośnych przy [math]x\rightarrow \pm\infty\, [/math]. Stosując oznaczenia identyczne jak w poprzednich zadaniach, obliczamy:
    [math] \lim_{x\rightarrow\infty}\frac{f(x)}{x}=1=:a_1 \, [/math]

    oraz

    [math] \lim_{x\rightarrow\infty} (f(x)-a_1 x)=0=:b_1\; . \, [/math]

    Prawą asymptotą jest więc prosta: [math]y=x\, [/math]. Dla lewej asymptoty otrzymujemy:

    [math] \lim_{x\rightarrow-\infty}\frac{f(x)}{x}=1=:a_2\; , \, [/math]

    a następnie:

    [math] \lim_{x\rightarrow-\infty} (f(x)-a_2 x)=0=:b_2\; . \, [/math]
    Lewa asymptota jest więc identyczną prostą: [math]y=x\, [/math].
  5. Punkty przecięcia z osiami współrzędnych. Miejscem zerowym funkcji jest [math]x_0=0\, [/math] i jest to zarazem punkt przecięcia wykresu z osią [math]y\, [/math].
  6. Pochodna funkcji. Obliczamy pochodną funkcji [math]f\, [/math]:
    [math] f'(x)=\frac{x^4-7x^2+10}{(x^2+1)^2}\; . \, [/math]
    Pochodna ta istnieje wszędzie (czyli [math]D'=\mathbb{R}\, [/math]).
  7. Przedziały monotoniczności i ekstrema funkcji. Mianownik wyrażenia (26) jest nieujemny, więc można go pominąć przy badaniu znaków pochodnej, natomiast licznik można zapisać w formie:
    [math] x^4-7x^2+10=(x^2-2)(x^2-5)=(x+\sqrt{2})(x-\sqrt{2})(x+\sqrt{5})(x-\sqrt{5})\; . \, [/math]

    Na tej podstawie łatwo stwierdzamy, że:

    1. dla [math]x\in ]-\infty,-\sqrt{5}[\,[/math] zachodzi [math]f'(x)\gt 0\;\; \Longrightarrow\;\,[/math] funkcja jest rosnąca,
    2. dla [math]x\in ]-\sqrt{5}, -\sqrt{2}[\,[/math] zachodzi [math]f'(x)\lt 0\;\; \Longrightarrow\;\,[/math] funkcja jest malejąca,
    3. dla [math]x\in ]-\sqrt{2}, \sqrt{2}[\,[/math] zachodzi [math]f'(x)\gt 0\;\; \Longrightarrow\;\,[/math] funkcja jest rosnąca.
    4. dla [math]x\in ]\sqrt{2},\sqrt{5}[\,[/math] zachodzi [math]f'(x)\lt 0\;\; \Longrightarrow\;\,[/math] funkcja jest malejąca,
    5. dla [math]x\in ]\sqrt{5},\infty[\,[/math] zachodzi [math]f'(x)\gt 0\;\; \Longrightarrow\;\,[/math] funkcja jest rosnąca.

    Ponadto [math]f'(x)=0\, [/math] dla [math]x=\pm\sqrt{5}\, [/math] oraz [math]x=\pm\sqrt{2}\, [/math]. Z otrzymanych rezultatów wynika, że:

    1. w punkcie [math]x=-\sqrt{5}\, [/math] funkcja ma maksimum, przy czym [math]\displaystyle f(-\sqrt{5})=-\frac{5\sqrt{5}}{2}\, [/math],
    2. w punkcie [math]x=-\sqrt{2}\, [/math] funkcja ma minimum, przy czym [math]\displaystyle f(-\sqrt{2})=-4\sqrt{2}\, [/math],
    3. w punkcie [math]x=\sqrt{2}\, [/math] funkcja ma maksimum, przy czym [math]\displaystyle f(\sqrt{2})=4\sqrt{2}\, [/math],
    4. a w punkcie [math]x=\sqrt{5}\, [/math] funkcja ma minimum, przy czym [math]\displaystyle f(-\sqrt{5})=\frac{5\sqrt{5}}{2}\, [/math].
    Wyniki te zgodne są z naszą obserwacją, że funkcja [math]f\, [/math] jest nieparzysta.
  8. Druga pochodna. Obliczamy teraz drugą pochodną:
    [math] f''(x)=18\,\frac{x(x^2-3)}{(x^2+1)^3}\; . \, [/math]
    Druga pochodna także istnieje wszędzie, więc mamy [math]D''=\mathbb{R}\, [/math].
  9. Wypukłość, wklęsłość, punkty przegięcia. Analizując znak wyrażenia (28), dochodzimy do wniosku, że:
    1. dla [math]x\in ]-\infty,-\sqrt{3}[\,[/math] zachodzi [math]f''(x)\lt 0\;\; \Longrightarrow\;\,[/math] funkcja jest wklęsła,
    2. dla [math]x\in ]-\sqrt{3}, 0[\,[/math] zachodzi [math]f''(x)\gt 0\;\; \Longrightarrow\;\,[/math] funkcja jest wypukła,
    3. dla [math]x\in ]0,\sqrt{3}[\,[/math] zachodzi [math]f''(x)\lt 0\;\; \Longrightarrow\;\,[/math] funkcja jest wklęsła,
    4. dla [math]x\in ]\sqrt{3},\infty[\,[/math] zachodzi [math]f''(x)\gt 0\;\; \Longrightarrow\;\,[/math] funkcja jest wypukła.
    W punktach [math]x=\pm \sqrt{3}\, [/math] oraz [math]x=0\, [/math] funkcja ma punkty przegięcia. Znajdziemy jeszcze wartości funkcji w tych punktach: [math]\displaystyle f(-\sqrt{3})=-\frac{13\sqrt{3}}{4}\, [/math], [math]f(0)=0\, [/math] oraz [math]\displaystyle f(\sqrt{3})=\frac{13\sqrt{3}}{4}\, [/math]. Ponownie możemy dostrzec w otrzymanych rezultatach odbicie nieparzystości funkcji.

Teraz wszystkie otrzymane informacje zbierzemy w formie tabeli.

[math]x\,[/math] [math]-\infty \, [/math] [math]-\sqrt{5}\, [/math] [math]-\sqrt{3}\, [/math] [math]-\sqrt{2}\, [/math] [math]0\, [/math] [math]\sqrt{2}\, [/math] [math]\sqrt{3}\,[/math] [math]\sqrt{5}\, [/math] [math]\infty\, [/math]
[math]f(x)\, [/math] [math]-\infty \, [/math] [math]-\frac{5\sqrt{5}}{2}\, [/math] [math]\searrow \, [/math] [math]-\frac{13\sqrt{3}}{4}\, [/math] [math]\searrow \, [/math] [math]-4\sqrt{2}\, [/math] [math]\nearrow \, [/math] [math]0\, [/math] [math]\nearrow \, [/math] [math]4\sqrt{2}\, [/math] [math]\searrow \, [/math] [math]\frac{13\sqrt{3}}{4}\, [/math] [math]\searrow \,[/math] [math]\frac{5\sqrt{5}}{2}\, [/math] [math]\nearrow \,[/math] [math]\infty \, [/math]
[math]f'(x)\, [/math] [math]+++\, [/math] [math]0\, [/math] [math]-\, [/math] [math]-\, [/math] [math]-\, [/math] [math]0\, [/math] [math]+\, [/math] [math]+\, [/math] [math]+\, [/math] [math]0\, [/math] [math]-\, [/math] [math]-\, [/math] [math]-\, [/math] [math]0\, [/math] [math]+++\, [/math]
[math]f''(x)\, [/math] [math]---\, [/math] [math]-\, [/math] [math]-\, [/math] [math]0\, [/math] [math]+\, [/math] [math]+\, [/math] [math]+\, [/math] [math]0\, [/math] [math]-\, [/math] [math]-\, [/math] [math]-\, [/math] [math]0\, [/math] [math]+\, [/math] [math]+\, [/math] [math]+++\, [/math]


Na jej podstawie można już łatwo sporządzić wykres funkcji, który przedstawiony jest na rysunku %i 3.

Wykres funkcji (20).


Zadanie 4

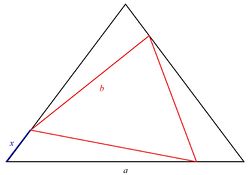
Znaleźć trójkąt równoboczny o najmniejszym polu, wpisany w inny trójkąt równoboczny o boku [math]a\, [/math].

Wskazówka

Zadanie bardzo łatwe, bez wskazówki.

Rozwiązanie

Oznaczmy symbolem [math]b\, [/math] długość boku wpisanego trójkąta. Odległość wierzchołków obu trójkątów oznaczymy [math]x\, [/math], tak jak jest to przedstawione na rysunku.

Rys 4. Trójkąt równoboczny o boku [math]b\, [/math] wpisany w trójkąt równoboczny o boku [math]a\, [/math].

Pole wpisanego trójkąta równe dane jest znanym wzorem:

[math] P=\frac{b^2\sqrt{3}}{4}\; . \, [/math]

Korzystając z twierdzenia cosinusów zastosowanego do któregoś z trójkątów o bokach [math]b\, [/math], [math]x\, [/math] oraz [math]a-x\, [/math], pole to wyrazimy poprzez wielkość [math]x\, [/math]:

[math] b^2=x^2+(a-x)^2-2x(a-x)\cos 60^{\circ}=3x^2-3ax+a^2\; . \, [/math]

Szukamy więc minimum funkcji:

[math] P(x)=\frac{\sqrt{3}}{4}(3x^2-3ax+a^2)\; . \, [/math]

Obliczając pochodną otrzymujemy:

[math] P'(x)=\frac{\sqrt{3}}{4}(6x-3a)\; . \, [/math]

Jedynym jej miejscem zerowym jest [math]\displaystyle x=\frac{a}{2}\, [/math]. Na lewo od tego punktu pochodna jest ujemna, a zatem funkcja malejąca, a na prawo pochodna dodatnia, czyli funkcja rosnąca. Widzimy, że faktycznie pole osiąga dla [math]\displaystyle x=\frac{a}{2}\, [/math] swoją minimalną wartość równą:

[math] P_{\mathrm{min}}=\frac{\sqrt{3}}{16}\, a^2\; . \, [/math]


Zadanie 5

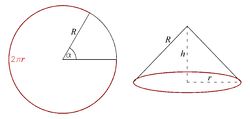
Dane jest koło o promieniu [math]R\, [/math]. Jaki wycinek, należy z niego usunąć, aby po sklejeniu uzyskać stożek o największej objętości?

Wskazówka

Należy wyrazić objętość stożka przez kąt [math]\alpha\, [/math] usuniętego wycinka, a następnie wykorzystać rachunek różniczkowy.

Rozwiązanie

Na rysunku przedstawiona jest sytuacja, z jaką mamy do czynienia i wprowadzone oznaczenia: [math]\alpha\, [/math] -- kąt usuniętego wycinka, [math]r\, [/math] -- promień podstawy stożka, [math]h\, [/math] -- jego wysokość.

Rys 5. Stożek uzyskany z koła, z którego usunięto wycinek o kacie [math]\alpha\, [/math].

Objętość stożka jest naturalnie dana wzorem:

[math] V=\frac{1}{3}\,\pi r^2 h\; . \, [/math]

Obwód podstawy stożka równy jest [math](2\pi-\alpha)R\, [/math], co daje promień jego postawy:

[math] r=\left(1-\frac{\alpha}{2\pi}\right)R\; . \, [/math]

Wysokość stożka możemy natomiast znaleźć z twierdzenia Pitagorasa wykorzystując fakt, że tworząca stożka ma długość [math]R\, [/math]:

[math] h^2+r^2=R^2\;\;\Longrightarrow \;\; h=R\sqrt{\frac{\alpha}{\pi}-\frac{\alpha^2}{4\pi^2}}\; . \, [/math]

Wstawiając to do (34) otrzymujemy szukaną funkcję [math]V(\alpha)\, [/math]:

[math] V(\alpha)=\frac{\sqrt{\pi}R^3}{3}\left(1-\frac{\alpha}{2\pi}\right)^2\sqrt{\alpha-\frac{\alpha^2}{4\pi}}\; . \, [/math]

Obliczamy teraz pochodną [math]V(\alpha)\, [/math] i szukamy ekstremów.

[math] V'(\alpha)=\frac{R^3}{24\pi^2}\cdot\frac{(2\pi-\alpha)(3\alpha^2-12\pi\alpha+4\pi^2)}{\sqrt{4\pi\alpha-\alpha^2}}\; . \, [/math]

Ze względów geometrycznych zachodzi: [math]0\lt \alpha\lt 2\pi\, [/math], co oznacza, że dla miejsc zerowych pochodnej oraz jej znaków istotne jest tylko wyrażenie: [math]3\alpha^2-12\pi\alpha+4\pi^2\, [/math]. Ma ono dwa miejsca zerowe, przy czym w przedziale [math]]0,2\pi[\, [/math] leży tylko [math]\displaystyle\alpha_1=2\pi-\frac{2\sqrt{6}}{3}\, \pi\, [/math]. W punkcie tym pochodna zmienia znak z dodatniej na ujemną, skąd wynika, że objętość dla [math]\alpha_1\, [/math] jest maksymalna. Podstawiając tę wartość do (37), otrzymujemy:

[math] V_{\mathrm{max}}=\frac{2\sqrt{3}\pi R^3}{27}\; . \, [/math]


Zadanie 6

Dana jest elipsa zapisana we współrzędnych biegunowych:

[math] r(\phi)=\frac{p}{1+e\,\cos \phi}\; , \, [/math]

gdzie [math]p\gt 0\, [/math] oraz [math]0\lt e\lt 1\, [/math]. Znaleźć półosie tej elipsy.

Wskazówka

Półoś [math]a\, [/math] (na osi [math]x\, [/math]) znaleźć jest łatwo, a półoś [math]b\, [/math] (na osi [math]y\, [/math]) znaleźć można szukając maksimum funkcji [math]y(\phi)\, [/math], gdzie [math]y\, [/math] jest zmienną kartezjańską.

Rozwiązanie

Wprowadzamy oznaczenia takie, jak na rysunku: [math]a\, [/math] -- duża półoś, [math]b\, [/math] -- mała półoś.

Rys 6. Elipsa opisana równaniem (40).

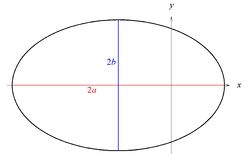
Aby znaleźć półoś [math]a\, [/math] nie ma potrzeby wykorzystywania rachunku różniczkowego. Wystarczy napisać:

[math] 2a=r(0)+r(\pi)=\frac{p}{1+e}+\frac{p}{1-e}=\frac{2p}{1-e^2}\;\; \Longrightarrow \;\; a=\frac{p}{1-e^2}\; . \, [/math]

W celu obliczenia półosi [math]b\, [/math] napiszemy równanie funkcji [math]y(\phi)\, [/math], gdzie [math]y\, [/math] jest zmienną kartezjańską, a [math]\phi\in[0,\pi]\,[/math]. Mamy:

[math] y(\phi)=r(\phi)\sin\phi=\frac{p\,\sin\phi}{1+e\,\cos\phi}\; . \, [/math]

Różniczkując tę funkcję po [math]\phi\, [/math], otrzymujemy:

[math] y'(\phi)=\frac{p(\cos\phi+e)}{(1+e\cos\phi)^2}\; . \, [/math]

Jedynym miejscem zerowym pochodnej (w przedziale [math]]0,\pi[\, [/math]) jest kąt stanowiący rozwiązanie równania: [math]\cos\phi=-e\, [/math]. W punkcie tym pochodna zmienia znak z dodatniej na ujemną, co oznacza, że mamy do czynienia z maksimum funkcji. Nie musimy znać jawnie tego kąta. Wystarczy nam znajomość wartości cosinusa oraz wiedza, że [math]\displaystyle\phi\in\left]\frac{\pi}{2},\pi\right[\, [/math], gdzie sinus jest dodatni. Wtedy wiemy, iż

[math] \sin\phi=\sqrt{1-\cos^2\phi}=\sqrt{1-e^2} \, [/math]

i wstawiając wszystkie potrzebne wartości do (42) uzyskujemy:

[math] b=y_{\mathrm{max}}=\frac{p\sqrt{1-e^2}}{1-e^2}=\frac{p}{\sqrt{1-e^2}}\; . \, [/math]


Zadanie 7

Pomiędzy ładunkami punktowymi [math]Q\, [/math] i [math]-8Q\, [/math] odległymi o [math]R\, [/math], znaleźć punkt, w którym siła elektrostatyczna działająca na pewien ładunek [math]q\, [/math] jest najmniejsza.

Wskazówka

Należy wykorzystać wzór na siłę elektrostatyczną działającą pomiędzy ładunkami punktowymi [math]q_1\, [/math] i [math]q_2\, [/math] odległymi o [math]r\, [/math]:

[math] F_{C}=\frac{1}{4\pi\epsilon_0}\cdot\frac{q_1\, q_2}{r^2}\; , \, [/math]

gdzie [math]\epsilon_0\, [/math] jest stałą.

Rozwiązanie

Całkowita siła, jaka działa na ładunek [math]q\, [/math] umieszczony pomiędzy ładunkami różnych znaków, jest ich algebraiczną sumą, gdyż oba wektory sił skierowane są w tę samą stronę. Wykorzystując wzór Coulomba:

[math] F_C=\frac{1}{4\pi\epsilon_0}\cdot\frac{q_1\, q_2}{r^2}\; , \, [/math]

gdzie [math]\epsilon_0\, [/math] jest stałą (współczynnikiem przenikalności elektrycznej próżni), [math]q_1\, [/math] i [math]q_2\, [/math] -- ładunkami, a [math]r\, [/math] -- odległością pomiędzy nimi, otrzymujemy:

[math] F=\frac{1}{4\pi\epsilon_0}\left(\frac{Q\, q}{x^2}+\frac{8\, Q\, q}{(R-x)^2}\right)\; . \, [/math]

Symbol [math]x\,[/math] oznacza tutaj odległość pomiędzy ładunkami [math]q\,[/math] i [math]Q\,[/math], a [math]R-x\,[/math] pomiędzy ładunkami [math]q\,[/math] i [math]-8Q\,[/math]. Musimy teraz znaleźć minimum tej funkcji (rolę argumentu odgrywa [math]x\, [/math]). W tym celu obliczamy pochodną:

[math] F'(x)=\frac{Q\, q}{4\pi\epsilon_0}\left(\frac{-2}{x^3}+\frac{16}{(R-x)^3}\right)\; . \, [/math]

Rozwiązując równanie [math]F'(x)=0\, [/math] otrzymujemy:

[math] \frac{1}{x^3}=\frac{8}{(R-x)^3}\;\; \Longrightarrow \;\; x=\frac{R}{3}\; . \, [/math]

Badając znaki pochodnej na lewo i na prawo od tego punktu, łatwo stwierdzamy, że siła przyjmuje w nim wartość minimalną. Jest ona równa:

[math] F_{\mathrm{min}}=\frac{27\, Q\, q}{4\pi\epsilon_0\, R^2}\; . \, [/math]


Źródło: „http://brain.fuw.edu.pl/edu/index.php?title=Matematyka_1NI/Badanie_funkcji&oldid=1231”