Matematyka 1NI/Ciągi rekurencyjne
Ciągi rekurencyjne
Zadanie 1
Znaleźć wzór ogólny i zbadać istnienie granicy ciągu określonego rekurencyjnie:
w dwóch przypadkach:
- dla [math]a_1=2\, [/math] i [math]\displaystyle a_2=\frac{10}{3}\, [/math],
- oraz dla [math]\displaystyle a_1=\frac{2}{3}\, [/math] i [math]\displaystyle a_2=\frac{2}{9}\, [/math].
Należy poszukiwać rozwiązania w postaci [math]A\, \lambda^n\, [/math], gdzie [math]A\, [/math] i [math]\lambda\, [/math] są stałymi.
Do równania rekurencyjnego (1) podstawmy [math]a_n\, [/math] w postaci [math]\lambda^n\, [/math], gdzie [math]\lambda\, [/math] jest pewną, różną od zera, stałą do wyznaczenia. Otrzymamy w ten sposób równanie:
Po uproszczeniu przez [math]\lambda^n\, [/math], uzyskamy równanie kwadratowe na [math]\lambda\, [/math]:
Równanie to ma dwa rozwiązania: [math]\displaystyle\lambda_1=\frac{1}{3}\, [/math] i [math]\lambda_2=3\, [/math].
Związek rekurencyjny (1) jest liniowy i jednorodny. Oznacza to, że jeśli pewien ciąg [math]a_n\, [/math] jest jego rozwiązaniem, to jest nim także [math]A\, a_n\, [/math], gdzie [math]A\, [/math] jest stałą. Z kolei jeśli znaleźlibyśmy dwa rozwiązania [math]a'_n\, [/math] oraz [math]a''_n\, [/math], to rozwiązaniem będzie także ich suma: [math]a'_n+a''_n\, [/math], a nawet kombinacja [math]A\, a'_n+B\, a''_n\, [/math], z dowolnymi stałymi [math]A\, [/math] oraz [math]B\, [/math]. Takie dwa rozwiązania otrzymaliśmy już powyżej: [math]\lambda_1^n\, [/math] oraz [math]\lambda_2^n\, [/math]. Wynika stąd, że ogólne rozwiązanie równania (1) ma postać:
Aby znaleźć stałe [math]A\, [/math] i [math]B\, [/math] wykorzystamy warunki początkowe.
- Musi zachodzić:
[math] a_1=\frac{1}{3}\,A+3 B=2\; ,\;\;\;\;\mathrm{oraz}\;\;\;\; a_2=\left(\frac{1}{3}\right)^2A+ 3^2B=\frac{10}{3}\; . \, [/math]
Rozwiązując ten układ równań ze względu na [math]A\, [/math] i [math]B\, [/math] otrzymujemy: [math]A=3\, [/math], [math]\displaystyle B=\frac{1}{3}\, [/math] i wzór na wyraz ogólny ciągu ma w tym przypadku postać:
[math] a_n=3\,\left(\frac{1}{3}\right)^n+\frac{1}{3}\,3^n=\left(\frac{1}{3}\right)^{n-1}+3^{n-1}\; . \, [/math]Ze względu na drugi człon, ciąg ten jest rozbieżny przy [math]n\rightarrow\infty\, [/math]. - Teraz muszą być spełnione warunki:
[math] a_1=\frac{1}{3}\, A+3B=\frac{2}{3}\; ,\;\;\;\;\mathrm{oraz}\;\;\;\; a_2=\left(\frac{1}{3}\right)^2A+3^2B=\frac{2}{9}\; . \, [/math]
Po rozwiązaniu tego układu widzimy, że [math]A=2\, [/math], [math]B=0\, [/math]. Wzór na wyraz ogólny ciągu ma teraz postać:
[math] a_n=2\,\left(\frac{1}{3}\right)^n+0\cdot 3^n=2\,\left(\frac{1}{3}\right)^n\; . \, [/math]Jasne jest, że w tym przypadku zachodzi:
[math] \lim_{n\rightarrow\infty}a_n=0\; . \, [/math]
Zadanie 2
Znaleźć wzór ogólny i zbadać istnienie granicy ciągu określonego rekurencyjnie:
dla [math]a_1=6\, [/math] i [math]a_2=16\, [/math].
Należy poszukiwać rozwiązania w postaci [math]A\, \lambda^n\, [/math], gdzie [math]A\, [/math] oraz [math]\lambda\, [/math] są stałymi.
Podobnie jak w poprzednim zadaniu, podstawimy do równania rekurencyjnego (10) [math]a_n\, [/math] w postaci [math]\lambda^n\, [/math], gdzie [math]\lambda\, [/math] jest pewną niezerową stałą. Otrzymamy w ten sposób równanie:
Po skróceniu obu stron przez [math]\lambda^n\, [/math], dochodzimy do równania kwadratowego na niewiadomą [math]\lambda\, [/math]:
Jedynym (ale za to podwójnym) jego rozwiązaniem jest [math]\lambda=2\, [/math].
Z poprzedniego zadania wiemy, że jeśli związek rekurencyjny jest liniowy i jednorodny (a tak jest w istocie w (10), to rozwiąznie ogólne jest kombinacją liniową rozwiązań szczególnych ([math]a'_n\, [/math], [math]a''_n\, [/math], [math]a'''_n\, [/math],...): [math]A\, a'_n+B\, a''_n+C\,a'''_n+\ldots\, [/math], z dowolnymi stałymi [math]A\, [/math], [math]B\, [/math], [math]C\, [/math],.... W naszym przypadku mamy dwa niezależne rozwiązania, gdyż rekurencja (10) jest rekurencją "o dwa". Jednym z tych rozwiązań jest, naturalnie, [math]\lambda^n\, [/math], a drugie ma postać [math]n\lambda^n\, [/math], o czym łatwo jest się przekonać wstawiając je do (10). Widzimy zatem, że ogólne rozwiązanie równania (10) ma postać:
Stałe [math]A\, [/math] i [math]B\, [/math] wyznaczymy z warunków początkowych:
Układ ten spełniony jest przez liczby [math]A=2\, [/math] oraz [math]B=1\, [/math] i, w konsekwencji:
Oczywiste jest, że ciąg ten jest rozbieżny.
Zadanie 3
Zbadać zbieżność ciągu określonego rekurencyjnie:
gdzie [math]a_1=1\, [/math].
Należy wykazać ograniczoność i monotoniczność ciągu.
Ciąg w treści zadania zdefiowany jest nieliniową rekurencją, którą można opisać wzorem:
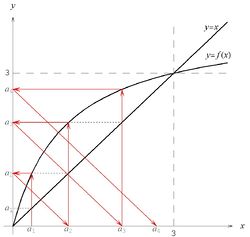
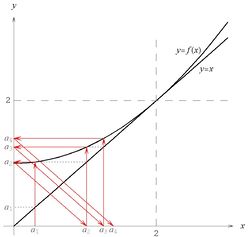
W tego typu problemach w ogólności nie potrafimy znaleźć jawnego wzoru na [math]a_n\, [/math] i musimy się ograniczyć do zbadania samej granicy. Wygodnie jest rozpocząć rozwiązywanie zadania od wykonania szkicu przebiegu funkcji [math]f\, [/math] podobnego do tego z rysunku 1. Przedstawiony jest na nim - przy użyciu czerwonych strzałek - sposób obliczania kolejnych wyrazów ciągu, przy czym punktem startowym jest [math]a_1\, [/math]. W treści zadania [math]a_1=1\, [/math], ale rysunek wygląda bardzo podobnie dla wszystkich [math]a_1\lt 3\, [/math] i został wykonany dla takiej jego wartości, dla której wygląda najbardziej przejrzyście. Punkt [math]x=3\, [/math] jest rozwiązaniem równania [math]x=f(x)\, [/math], a zatem jest punktem stałym odwzorowania [math]f\, [/math].
Rysunek ten sugeruje, że nasz ciąg po pierwsze jest ograniczony z góry przez liczbę [math]3\, [/math], a po drugie - rosnący. Te dwie jego własności poniżej udowodnimy.
- Ograniczoność.
Ograniczoność ciągu wykażemy, korzystając z metody indukcji matematycznej.- Dla [math]n=1\, [/math] mamy [math]a_1=1\lt 3\, [/math].
- Teraz dowodzimy następującej implikacji:
[math] a_n\lt 3\;\;\;\Longrightarrow \;\;\; a_{n+1}\lt 3\; . \, [/math]
Znajdźmy znak wyrażenia [math]a_{n+1}-3\, [/math]:
[math] a_{n+1}-3=\frac{4a_n}{a_n+1}-3=\frac{a_n-3}{a_n+1}\lt 0\; , \, [/math]przy czym ostatnia nierównosć wynika z założenia indukcyjnego.
Ciąg jest więc w istocie ograniczony:
[math] \forall_{n\in\mathbb{N}}\;\; a_n\lt 3\; . \, [/math]
- Monotoniczność.
Obliczymy różnicę dwóch kolejnych wyrazów ciągu:[math] a_{n+1}-a_n=\frac{4a_n}{a_n+1}-a_n=\frac{a_n(3-a_n)}{a_n+1}\gt 0\; . \, [/math]Końcowa nierówność wynika z wykazanej wyżej własności (20) i oznacza, że nasz ciąg jest rosnący.
Jak wiadomo w zbiorze liczb rzeczywistych ciąg monotoniczny i ograniczony ma granicę. Oznaczmy ją literą [math]g\, [/math]. Skoro granica ta istnieje to możemy po obu stronach równania (16) przejść z [math]n\, [/math] do nieskończoności, otrzymując równanie:
które ma dwa rozwiązania: [math]g=0\, [/math] lub [math]g=3\, [/math]. Tylko jedna z tych dwóch liczb może być granicą ciągu [math]a_n\, [/math]. Jednakże rosnący ciąg liczb dodatnich nie może być zbieżny do zera. Stąd:
Zadanie 4
Zbadać zbieżność ciągu określonego rekurencyjnie:
gdzie [math]a_1=6\, [/math].
Należy wykazać ograniczoność i monotoniczność ciągu.
Ponownie mamy do czynienia z nieliniową rekurencją opisaną wzorem:
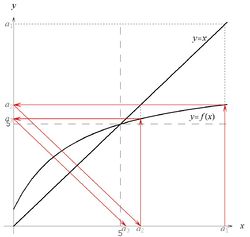
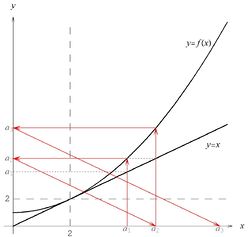
Przebieg funkcji [math]f\, [/math] przedstawiony jest na rysunku 2. Punktem startowym jest w tym zadaniu [math]a_1=6\, [/math], ale rysunek - podobnie jak w poprzednim zadaniu - został wykonany dla innej wartości, dla której wygląda bardziej przejrzyście, a zasadnicze własności ciągu (którymi zajmiemy się poniżej) przy tym się nie zmieniają. Punkt [math]x=5\, [/math] jest rozwiązaniem równania [math]x=f(x)\, [/math], a zatem jest punktem stałym odwzorowania [math]f\, [/math].
Z rysunku możemy się zorientować, że ciąg [math]a_n\, [/math] jest ograniczony z dołu przez liczbę [math]5\, [/math] oraz że jest malejący, co poniżej ściśle wykażemy.
- Ograniczoność.
Tak jak poprzednio ograniczoność ciągu udowodnimy metodą indukcji matematycznej.- Dla [math]n=1\, [/math] mamy [math]a_1=6\gt 5\, [/math].
- Teraz dowodzimy implikacji:
[math] a_n\gt 5\;\;\;\Longrightarrow \;\;\; a_{n+1}\gt 5 \, [/math]
Znajdziemy znak wyrażenia [math]a_{n+1}-5\, [/math]:
[math] a_{n+1}-5=5\,\frac{3a_n+1}{2a_n+6}-5=5\,\frac{a_n-5}{2a_n+6}\gt 0\; . \, [/math]Otrzymana nierówność wynika z założenia indukcyjnego.
Ciąg [math]a_n\, [/math] jest więc faktycznie ograniczony z dołu:
[math] \forall_{n\in\mathbb{N}}\;\; a_n\gt 5\; . \, [/math] - Monotoniczność.
Obliczymy teraz różnicę dwóch kolejnych wyrazów ciągu:[math] a_{n+1}-a_n=5\,\frac{3a_n+1}{2a_n+6}-a_n=-2\frac{(a_n-5)(a_n+\frac{1}{2})}{2a_n+6}\; . \, [/math]Wyrażenie to jest ujemne, co jest konsekwencją własności (28) i oznacza, że ciąg jest malejący.
Ciąg monotoniczny i ograniczony ma na pewno granicę, którą oznaczymy literą [math]g\, [/math]. Skoro granica ta istnieje, to możemy po obu stronach równania (24) przejść z [math]n[/math] do nieskończoności, otrzymując:
Równanie to ma dwa rozwiązania: [math]\displaystyle g=-\frac{1}{2}\, [/math] lub [math]g=5\, [/math] i tylko jedna z tych liczb może być granicą ciągu [math]a_n\, [/math]. Ciąg ograniczony z dołu przez liczbę [math]5\, [/math] nie może być jednak zbieżny do [math]\displaystyle -\frac{1}{2}\, [/math]. Stąd wynika, że:
Zadanie 5
Zbadać zbieżność ciągu określonego rekurencyjnie:
gdzie [math]a_1=1\, [/math].
Należy rozłożyć ciąg na dwa podciągi ograniczone i monotoniczne.
Rekurencja tym razem opisana jest wzorem:
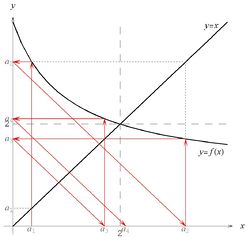
Przebieg funkcji [math]f\, [/math] przedstawiony jest na rysunku 3. Jest ona w interesującym nas przedziale malejąca, a ciąg wydaje się oscylować wokół punktu [math]x=2\, [/math], który jest rozwiązaniem równania [math]x=f(x)\, [/math] i jednocześnie kandydatem na granicę ciągu [math]a_n\, [/math]. Rysunek ten mówi nam, że musimy zmienić nasz sposób postępowania w stosunku do poprzednich zadań, gdyż w tym przykładzie nie mamy do czynienia z ciągiem monotonicznym. Jednakże można mieć nadzieję, że monotoniczne (i ograniczone) okażą się jego podciągi: ten o indeksach parzystych, czyli [math]a_{2k}\, [/math] oraz ten o indeksach nieparzystych, czyli [math]a_{2k-1}\, [/math], gdzie [math]k=1,2,3,\ldots\, [/math].
Musimy więc zacząć od przekształcenia rekurencji (32) w rekurencję "o dwa":
i rozpatrzenia kolejno podciągów "parzystego" i "nieparzystego".
- Ciąg o indeksach parzystych.
Mamy następującą rekurencję ("o jeden") w zmiennej [math]k\, [/math]:[math] a_{2(k+1)}=f_p(a_{2k})\; ,\;\;\;\;\mathrm{gdzie}\;\;\;\; f_p(x)=\frac{5x+8}{2x+5}\; . \, [/math]Z rysunku możemy wnosić, że ciąg ten jest malejący i ograniczony z dołu przez liczbę [math]2\, [/math] ([math]x=2\, [/math] jest punktem stałym funkcji [math]f\, [/math], ale także [math]f_p\, [/math]). Wykażemy poniżej, że tak jest w istocie.
- Ograniczoność.
Ograniczoność ciągu udowodnimy --- jak zwykle --- metodą indukcji matematycznej.- Dla [math]k=1\, [/math] mamy [math]\displaystyle a_2=\frac{5}{2}\gt 2\, [/math].
- Teraz dowiedziemy prawdziwości implikacji:
[math] a_{2k}\gt 2\;\;\;\Longrightarrow \;\;\; a_{2(k+1)}\gt 2\; . \, [/math]
Znajdziemy znak wyrażenia [math]a_{2(k+1)}-2\, [/math]:
[math] a_{2(k+1)}-2=\frac{5a_{2k}+8}{2a_{2k}+5}-2=\frac{a_{2k}-2}{2a_{2k}+5}\gt 0\; , \, [/math]gdzie ostatnia nierówność wynika z założenia indukcyjnego.
Ciąg [math]a_{2k}\, [/math] jest więc rzeczywiście ograniczony z dołu:
[math] \forall_{k\in\mathbb{N}}\;\; a_{2k}\gt 2\; . \, [/math] - Monotoniczność.
Obliczymy teraz różnicę dwóch kolejnych wyrazów ciągu:[math] a_{2(k+1)}-a_{2k}=\frac{5a_{2k}+8}{2a_{2k}+5}-a_{2k}=2\,\frac{(2-a_{2k})(2+a_{2k})}{2a_{2k}+5}\lt 0\; , \, [/math]co wynika z (38) i oznacza, że ciąg jest malejący.
Ciąg monotoniczny i ograniczony ma granicę, którą oznaczymy literą [math]g_p\, [/math]. Skoro granica ta istnieje to możemy po obu stronach równania (35) przejść z [math]k\, [/math] do nieskończoności, otrzymując:
[math] g_p=\frac{5g_p+8}{2g_p+5}\; . \, [/math]Równanie to ma dwa rozwiązania: [math]-2\, [/math] oraz [math]2\, [/math], ale granicą musi być ta druga liczba, gdyż [math]a_{2k}\,[/math] jest ograniczony z dołu przez dwójkę. Mamy zatem:
[math] g_p=\lim_{k\rightarrow\infty}a_{2k}=2\; . \, [/math]
- Ograniczoność.
- Ciąg o indeksach nieparzystych.
Mamy teraz rekurencję w zmiennej [math]k\, [/math]:[math] a_{2k+1}=f_n(a_{2k-1})\; ,\;\;\;\;\mathrm{gdzie}\;\;\;\; f_n(x)=\frac{5x+8}{2x+5}\; . \, [/math]Na podstawie rysunku wydaje się, że ciąg ten powinien być rosnący i ograniczony z góry przez liczbę [math]2\, [/math].
- Ograniczoność.
Ograniczoność ciągu wykażemy ponownie metodą indukcji matematycznej.- Dla [math]k=1\, [/math] mamy [math]\displaystyle a_1=1\lt 2\, [/math].
- Teraz dowiedziemy, że:
[math] a_{2k-1}\lt 2\;\;\;\Longrightarrow \;\;\; a_{2k+1}\lt 2\; . \, [/math]
Następnie rozpatrzymy wyrażenie [math]a_{2k+1}-2\, [/math]:
[math] a_{2k+1}-2=\frac{5a_{2k-1}+8}{2a_{2k-1}+5}-2=\frac{a_{2k-1}-2}{2a_{2k-1}+5}\lt 0\; . \, [/math]
Jak widzimy, ciąg [math]a_{2k-1}\, [/math] jest ograniczony z góry:
[math] \forall_{k\in\mathbb{N}}\;\; a_{2k-1}\lt 2\; . \, [/math]
- Monotoniczność.
Różnica dwóch kolejnych wyrazów ciągu wyraża się wzorem analogicznym do (39) :[math] a_{2k+1}-a_{2k-1}=\frac{5a_{2k-1}+8}{2a_{2k-1}+5}-a_{2k-1}=2\,\frac{(2-a_{2k-1})(2+a_{2k-1})}{2a_{2k-1}+5}\; , \, [/math]i jest dodatnia, co jest konsekwencją (45).
Mamy do czynienia z ciągiem ograniczonym i monotonicznym, a zatem ma on granicę ([math]g_n\, [/math]). Przechodąc z [math]k\, [/math] do nieskończoności po obu stronach równania (42) otrzymujemy:
[math] g_n=\frac{5g_n+8}{2g_n+5}\; . \, [/math]Jest to równanie identyczne do (40) i oczywiście ma takie same rozwiązania. Mamy więc:
[math] g_n=\lim_{k\rightarrow\infty}a_{2k-1}=2\; . \, [/math]Ponieważ [math]g_p=g_n=2\, [/math], więc oba podciągi zbieżne są do tej samej granicy. Jest to też granica samego ciągu [math]a_n\, [/math], gdyż do podciągu "parzystego" i "nieparzystego" należą wszystkie wyrazy ciągu (wystarczyłoby nawet, gdyby należały tylko prawie wszystkie).
- Ograniczoność.
Udowadniamy najpierw, że [math] \forall n \in \mathbb{N}: \, a_n\gt 1 [/math] (prosty dowód indukcyjny). Jak już wiemy kandydatem na granicę jest 2. Zapiszmy różnicę [math] a_{n+1}-2 [/math] następująco
[math] a_{n+1}-2 = \frac{a_n+4}{a_n+1} -2=-\frac{a_n-2}{a_n+1} [/math]
W liczniku odtworzyła nam się różnica [math] a_{n+1}-2 [/math] dla wyrazu wcześniejszego! Mamy dla dowolnego [math] n[/math]
[math] |a_{n+1}-2|= \frac{|a_n-2|}{a_n+1}\lt \frac{1}{2}|a_n-2|[/math] skąd otrzymujemy
[math] |a_{n+1}-2|\lt \frac{1}{2^n}|a_1-2|[/math]. Wyrażenie po prawej stronie nierówności zbiega do zera wobec tego z twierdzenia o trzech ciągach mamy [math] \lim_{n\rightarrow\infty}a_{n+1}=2. [/math]
Zadanie 6
Zbadać zbieżność ciągu określonego rekurencyjnie:
gdzie [math]a_1\gt 1\, [/math].
Należy rozłożyć ciąg na dwa podciągi ograniczone i monotoniczne.
Rekurencja dana jest wzorem:
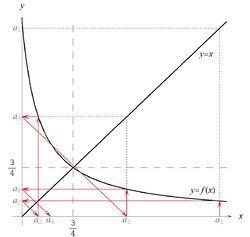
Wykres funkcji [math]f\, [/math] przedstawiony jest na rysunku 4 i, jak widać, dla dodatnich wartości [math]x\, [/math] jest ona malejąca. W konsekwencji ciąg [math]a_n\, [/math] oscyluje wokół punktu [math]\displaystyle x=\frac{3}{4}\, [/math], który jest rozwiązaniem równania [math]x=f(x)\, [/math] i może ewentualnie stanowić jego granicę. Postąpimy więc podobnie jak poprzednio - rozłożymy ciąg na dwa podciągi: [math]a_{2k}\, [/math] oraz [math]a_{2k-1}\, [/math], gdzie [math]k=1,2,3,\ldots\, [/math].
Przekształcimy teraz rekurencję (49) na rekurencję "o dwa":
i badać będziemy osobno podciągi "parzysty" i "nieparzysty".
- Ciąg o indeksach parzystych.
Mamy następującą rekurencję ("o jeden") w zmiennej [math]k\, [/math]:[math] a_{2(k+1)}=f_p(a_{2k})\; ,\;\;\;\;\mathrm{gdzie}\;\;\;\; f_p(x)=\frac{12x+3}{4x+13}\; . \, [/math]Z rysunku wynika, że ciąg ten powinien być rosnący i ograniczony z góry przez liczbę [math]\displaystyle\frac{3}{4}\, [/math] (punkt stały dla funkcji [math]f\, [/math] oraz [math]f_p\, [/math]). Wykażemy te własności poniżej.
- Ograniczoność.
Znów stosujemy indukcję matematyczną.- Dla [math]k=1\, [/math] mamy: [math]\displaystyle a_2=\frac{3}{4a_1+1}\lt \frac{3}{5}\lt \frac{3}{4}\, [/math], gdyż [math]a_1\gt 1\, [/math].
- Teraz wykazujemy, że:
[math] a_{2k}\lt \frac{3}{4}\;\;\;\Longrightarrow \;\;\; a_{2(k+1)}\lt \frac{3}{4}\; . \, [/math]
Zbadamy znak wyrażenia [math]\displaystyle a_{2(k+1)}-\frac{3}{4}\, [/math]:
[math] a_{2(k+1)}-\frac{3}{4}=\frac{12a_{2k}+3}{4a_{2k}+13}-\frac{3}{4}=9\,\frac{a_{2k}-\frac{3}{4}}{4a_{2k}+13}\lt 0\; . \, [/math]
Ciąg [math]a_{2k}\, [/math] jest więc ograniczony z góry:
[math] \forall_{k\in\mathbb{N}}\;\; a_{2k}\lt \frac{3}{4}\; . \, [/math]
- Monotoniczność.
Obliczymy różnicę dwóch kolejnych wyrazów ciągu:[math] a_{2(k+1)}-a_{2k}=\frac{12a_{2k}+3}{4a_{2k}+13}-a_{2k}=4\,\frac{(\frac{3}{4}-a_{2k})(a_{2k}+1)}{4a_{2k}+13}\gt 0\; , \, [/math]co wynika z (55). Oznacza to, że badany podciąg jest rosnący.
Podciąg "parzysty" jest monotoniczny i ograniczony, a zatem ma granicę ([math]g_p\, [/math]). Liczba ta spełnia równanie:
[math] g_p=\frac{12g_p+3}{4g_p+13}\; , \, [/math]które ma dwa rozwiązania: [math]-1\, [/math] oraz [math]\displaystyle \frac{3}{4}\, [/math], przy czym ta druga liczba jest szukaną granicą podciągu [math]a_{2k}\, [/math]:
[math] g_p=\lim_{k\rightarrow\infty}a_{2k}=\frac{3}{4}\; . \, [/math] - Ograniczoność.
- Ciąg o indeksach nieparzystych.
Mamy teraz następującą rekurencję w zmiennej [math]k\, [/math]:[math] a_{2k+1}=f_n(a_{2k-1})\; ,\;\;\;\;\mathrm{gdzie}\;\;\;\; f_n(x)=\frac{12x+3}{4x+13}\; . \, [/math]Na podstawie rysunku podejrzewamy, że podciąg ten jest malejący i ograniczony z dołu przez liczbę [math]\frac{3}{4}\, [/math].
- Ograniczoność.
- Dla [math]k=1\, [/math] mamy [math]\displaystyle a_1\gt 1\gt \frac{3}{4}\, [/math].
- Teraz musimy dowieść, że:
[math] a_{2k-1}\gt \frac{3}{4}\;\;\;\Longrightarrow \;\;\; a_{2k+1}\gt \frac{3}{4}\; . \, [/math]
Rozpatrzymy wyrażenie [math]\displaystyle a_{2k+1}-\frac{3}{4}\, [/math]:
[math] a_{2k+1}-\frac{3}{4}=\frac{12a_{2k-1}+3}{4a_{2k-1}+13}-\frac{3}{4}=9\, \frac{a_{2k-1}-\frac{3}{4}}{4a_{2k-1}+13}\gt 0\; . \, [/math]
Podciąg [math]a_{2k-1}\, [/math] jest więc ograniczony z dołu:
[math] \forall_{k\in\mathbb{N}}\;\; a_{2k-1}\gt \frac{3}{4}\; . \, [/math] - Monotoniczność.
Różnica dwóch kolejnych wyrazów ciągu wyraża się wzorem podobnym do (56):[math] a_{2k+1}-a_{2k-1}=\frac{12a_{2k-1}+3}{4a_{2k-1}+13}-a_{2k-1}=4\,\frac{(\frac{3}{4}-a_{2k-1})(a_{2k-1}+1)}{4a_{2k-1}+13}\lt 0\; . \, [/math]
Mamy więc do czynienia z podciągiem ograniczonym i monotonicznym, a zatem ma on granicę ([math]g_n\, [/math]) spełniającą równanie:
[math] g_n=\frac{12g_n+3}{4g_n+13}\; . \, [/math]Jest to równanie identyczne do (57) i oczywiście ma takie same rozwiązania. Otrzymujemy więc:
[math] g_n=\lim_{k\rightarrow\infty}a_{2k-1}=\frac{3}{4}\; . \, [/math]Jak widzimy [math]\displaystyle g_p=g_n=\frac{3}{4}\, [/math], więc oba podciągi mają tę samą granicę. Podobnie jak w poprzednim przykładzie wnosimy stąd, że jest ona też granicą samego ciągu [math]a_n\, [/math].
- Ograniczoność.
Zadanie 7
Zbadać zbieżność ciągu określonego rekurencyjnie:
dla przypadków:
- [math]0\lt a_1\lt 2\, [/math].
- [math]a_1\gt 2\, [/math].
Należy zbadać, czy ciąg jest ograniczony i monotoniczny.
Rekurencja w tym przypadku dana jest wzorem:
Zbadamy, czy uda się wykazać, że ciąg jest monotoniczny i ograniczony.
- [math]0\lt a_1\lt 2\, [/math].
Przebieg funkcji [math]f\, [/math] przedstawiony jest na rysunku 5a, gdzie zaznaczone zostały także kolejne wyrazy ciągu. Szkic ten podpowiada nam, że ciąg [math]a_n\, [/math] jest rosnący i ograniczony z góry przez dwójkę (która jest jedynym punktem stałym odwzorowania [math]f\, [/math]), co postaramy się poniżej udwowodnić.- Ograniczoność.
Ograniczoność ciągu wykażemy korzystając, jak zwykle, z indukcji matematycznej.- Dla [math]n=1\, [/math] mamy [math]0\lt a_1\lt 2\, [/math].
- Teraz dowodzimy następującej implikacji:
[math] a_n\lt 2\;\;\;\Longrightarrow \;\;\; a_{n+1}\lt 2\; . \, [/math]
Znajdziemy znak wyrażenia [math]a_{n+1}-2\, [/math]:
[math] \begin{array}{ccl} a_{n+1}-2&\!\!\! =&\!\!\! \displaystyle\frac{1}{4}\,a_n^2+1-2\\ &\!\!\! =&\!\!\! \displaystyle\frac{1}{4}(a_n-2)(a_n+2)\lt 0\; ,\end{array} \, [/math]co wynika z założenia indukcyjnego.
Ciąg jest więc rzeczywiście ograniczony:
[math] \forall_{n\in\mathbb{N}}\;\; a_n\lt 2\; . \, [/math] - Monotoniczność.
Obliczymy różnicę dwóch kolejnych wyrazów ciągu:[math] a_{n+1}-a_n=\frac{1}{4}\,a_n^2+1-a_n=\frac{1}{4}\,(a_n-2)^2\gt 0\; . \, [/math]Ciąg jest więc rosnący. Zauważmy, że w przeciwieństwie do poprzednich przykładów, ostatnia nierówność jest prawdziwa niezależnie od tego, czy [math]a_n\lt 2\, [/math], czy [math]a_n\gt 2\, [/math], więc słuszna będzie ona także w podpunkcie b.
Wynika stąd, że ciąg ma granicę i spełnia ona równanie:
[math] g=\frac{1}{4}\, g^2+1\; , \, [/math]którego jedynym rozwiazaniem jest [math]g=2\, [/math]. Liczba ta musi więc być szukaną granicą ciągu:
[math] \lim_{n\rightarrow\infty}a_n=2\; . \, [/math] - Ograniczoność.
- [math]a_1\gt 2\, [/math].
Sytuacja, z jaką mamy teraz do czynienia, przedstawiona jest na rysunku 5b. Kolejne wyrazy ciągu "uciekają" od punktu stałego, a kolejnego punktu stałego odwzorowanie [math]f\, [/math] nie ma. To że ciąg jest rzeczywiście rosnący, wykazaliśmy już zresztą w ścisły sposób w punkcie a. Wiedza ta wystarcza nam do wyciagnięcia wniosku, że ciąg jest rozbieżny. Granicą może być bowiem tylko punkt stały, a innego takiego punktu poza dwójką nie ma. Rosnący ciąg liczb [math]a_1, a_2, a_3, \ldots\, [/math], dla którego [math]a_1\gt 2\, [/math] nie może być jednak zbieżny do [math]2\, [/math].