Matematyka 1NI/Kąty przecięcia krzywych
Kąty przecięcia krzywych
Zadanie 1
Znaleźć kąty, pod jakimi przecinają się wykresy funkcji [math]f(x)=\mathrm{tg}\, x\, [/math] oraz [math]g(x)=\mathrm{ctg}\, x\, [/math].
Należy obliczyć pochodne obu funkcji w punktach przecięcia.
Najpierw znajdziemy współrzędne punktów przecięcia. W tym celu rozwiązujemy równanie:
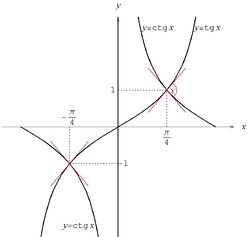
Ze względu na okresowość obu funkcji (z okresem równym [math]\pi\, [/math]) wystarczy ograniczyć się do argumentów z przedziału [math]\displaystyle \left]-\frac{\pi}{2},\frac{\pi}{2}\right[\, [/math]. Równanie (1) ma wówczas dwa rozwiązania: [math]\displaystyle x=\pm\frac{\pi}{4}\, [/math]. Ponieważ funkcje [math]f\, [/math] i [math]g\, [/math] są nieparzyste, więc w obu tych punktach kąt przecięcia będzie identyczny. Poniżej rozważymy zatem jedynie przypadek [math]\displaystyle x=\frac{\pi}{4}\, [/math]. Sytuacja, z jaką mamy do czynienia, przedstawiona jest na rysunku 1.
Aby znaleźć współczynniki kierunkowe stycznych obliczamy pochodne obu funkcji (kąty nachylenia wykresów funkcji [math]f\, [/math] i [math]g\, [/math] oznaczamy odpowiednio symbolami [math]\alpha\, [/math] i [math]\beta\, [/math]):
Szukany kąt [math]\gamma=\alpha-\beta\, [/math]. Posługując się wzorem na tangens różnicy kątów, mamy więc:
Tangens kąta [math]\gamma\, [/math] okazał się być ujemny, więc sam kąt jest większy od [math]\displaystyle \frac{\pi}{2}\, [/math]. Posługując się kalkulatorem możemy znaleźć jego przybliżoną wartość: [math]\gamma\approx 2.214 \,\mathrm{rad}\, [/math].
Zadanie 2
Znaleźć kąty, pod jakimi przecinają się wykresy funkcji [math]f(x)=x^2\, [/math] oraz [math]g(x)=\sqrt{x}\, [/math].
Należy obliczyć pochodne obu funkcji w punktach przecięcia.
Współrzędne punktów przecięcia znajdziemy, rozwiązując równanie:
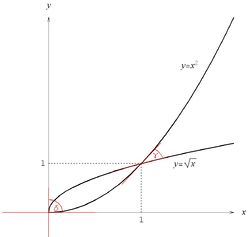
Ma ono dwa rozwiązania: [math]x=0\, [/math] oraz [math]x=1\, [/math], co przedstawione zostało na rysunku 2.
- [math]x=0.\;\;\;\, [/math] Aby znaleźć współczynniki kierunkowe stycznych (kąty nachylenia wykresów funkcji [math]f\, [/math] i [math]g\, [/math] oznaczamy odpowiednio symbolami [math]\alpha\, [/math] i [math]\beta\, [/math]) obliczamy pochodne. Najpierw znajdujemy
[math] \mathrm{tg}\,\alpha =\left.f'(x)\right|_{x=0}=\left.2x\right|_{x=0}=0\; , \, [/math]
co oznacza, że [math]\alpha=0\, [/math]. Natomiast pochodna (oczywiście mówić możemy wyłącznie o pochodnej prawostronnej) funkcji [math]g\, [/math] w tym punkcie nie istnieje. Z rysunku widać jednoznacznie, dlaczego tak się dzieje. Otóż styczna do wykresu staje się w tym punkcie pionowa i współczynnik kierunkowy dąży do nieskończoności. Wynika stąd, iż [math]\displaystyle\beta =\frac{\pi}{2}\, [/math]. Otrzymujemy więc [math]\displaystyle\delta=\alpha-\beta=-\frac{\pi}{2}\, [/math]. Krzywe przecinają się zatem pod kątem prostym.
- [math]x=1.\;\;\;\, [/math] Tym razem mamy:
Korzystając z wzoru na tangens różnicy kątów otrzymujemy:
Zadanie 3
Znaleźć kąty, pod jakimi przecinają się wykresy funkcji [math]f(x)=x^2\, [/math] oraz [math]g(x)=x^4-2\, [/math].
Należy obliczyć pochodne obu funkcji w punktach przecięcia.
Współrzędne punktów przecięcia otrzymamy z równania:
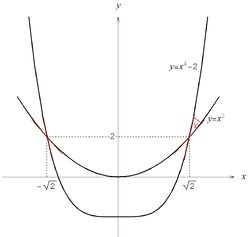
które ma dwa rozwiązania: [math]x=\pm\sqrt{2}\, [/math]. Ze względu na parzystość obu funkcji, poniżej zajmiemy się wyłącznie przypadkiem [math]x=\sqrt{2}\, [/math]. Odpowiednie wykresy przedstawia rysunek 3.
Aby znaleźć współczynniki kierunkowe stycznych, obliczamy pochodne funkcji [math]f\, [/math] i [math]g\, [/math]. Kąty nachylenia ich wykresów oznaczamy odpowiednio symbolami [math]\alpha\, [/math] i [math]\beta\, [/math]. Otrzymujemy:
Podobnie jak w poprzednich zadaniach, korzystamy teraz z wzoru na tangens różnicy kątów, otrzymując:
W przybliżeniu znajdujemy, że: [math]\gamma\approx 0.252 \,\mathrm{rad}\, [/math].
Zadanie 4
Wykazać, że rodziny krzywych:
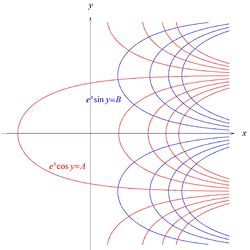
gdzie [math]A\, [/math] i [math]B\, [/math] są stałymi różnymi od zera, przecinają się wszędzie pod kątem prostym.
Należy znaleźć pochodne obu (niejawnych) funkcji [math]y(x)\, [/math] w punktach przecięcia, różniczkując równania (11).
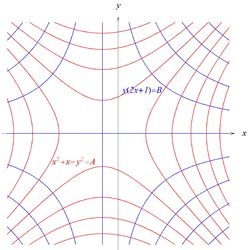
Równania (11) opisują hiperbole, które przestawione są na rysunku 4.
Definiują one pewne funkcje [math]y(x)\, [/math]. Zakładając, że są one różniczkowalne, możemy kolejno napisać:
Wielkości te istnieją w interesujących nas punktach, gdyż drugie z równań (11) wyklucza, aby na drugiej z krzywych (a więc także w punktach przecięcia) zachodziło [math]y=0\, [/math] bądź [math]\displaystyle x=-\frac{1}{2}\, [/math] (pamiętamy, że [math]B\neq 0\, [/math]).
Przyjmijmy, że dany punkt przecięcia ma współrzędne [math](x_0,y_0)\, [/math]. Wówczas kąty ([math]\alpha\, [/math], [math]\beta\, [/math]) nachylenia obu krzywych dane są równaniami:
Ponieważ [math]\displaystyle -\frac{\pi}{2}\lt \alpha,\beta \lt \frac{\pi}{2}\, [/math], wiec z równania tego wynika, iż [math]\displaystyle \alpha-\beta=\pm\frac{\pi}{2}\, [/math].
Zadanie 5
Wykazać, że rodziny krzywych:
gdzie [math]A,B\gt 0\, [/math], przecinają się wszędzie pod kątem prostym.
Należy znaleźć pochodne obu (niejawnych) funkcji [math]y(x)\, [/math] w punktach przecięcia, różniczkując równania (14).
Na początku zastanowimy się, czy krzywe (14) przecinają się dla dowolnych [math]A,B\gt 0\, [/math]. W tym celu podzielimy oba równania stronami, otrzymując kolejne równanie:
które ma zawsze rozwiązanie. Z (14) możemy ponadto otrzymać inny związek:
skąd uzyskujemy:
Krzywe opisane równaniami (14) mają więc punkty przecięcia, a cały ich przebieg przestawiony są na rysunku 5.
Związki (14) definiują pewne (niejawne) funkcje [math]y(x)\, [/math]. Przyjmując, że są one różniczkowalne, możemy napisać:
Równania (14) wraz z warunkiem [math]A,B\gt 0\, [/math] wykluczają, aby zachodziło [math]\displaystyle y=n\,\frac{\pi}{2}[/math] dla [math]n\in\mathbb{Z}\, [/math], więc obie pochodne istnieją w każdym punkcie przecięcia.
Przyjmijmy, że dany punkt przecięcia ma współrzędne [math](x_0,y_0)\, [/math]. Kąty ([math]\alpha\, [/math], [math]\beta\, [/math]) nachylenia obu krzywych dane są równaniami:
Ponieważ [math]\displaystyle -\frac{\pi}{2}\lt \alpha,\beta \lt \frac{\pi}{2}\, [/math], więc z powyższego związku wynika, iż [math]\displaystyle \alpha-\beta=\pm\frac{\pi}{2}\, [/math].
Zadanie 6
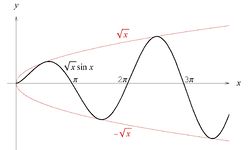
Wykazać, że wykresy funkcji [math]f_1(x)=\sqrt{x}\, [/math], [math]f_2(x)=-\sqrt{x}\, [/math] oraz [math]g(x)=\sqrt{x}\sin x\, [/math] są styczne we wszystkich punktach wspólnych (poza początkiem układu współrzędnych).
Należy obliczyć i porównać pochodne funkcji w punktach wspólnych.
Wykresy wszystkich funkcji przedstawione są na rysunku 6.
Równanie [math]f_1(x)=g(x)\, [/math] daje [math]\sin x=1\, [/math] i widzimy, że punkty wspólne możemy numerować zmienną [math]n=0,1,2,\ldots\, [/math]. Mają one postać: [math]\displaystyle x_n=\frac{\pi}{2}+2 n\pi\, [/math]. W tych punktach otrzymujemy:
gdyż [math]\cos x_n=0\, [/math]. Jak widzimy pochodne są identyczne, a zatem wykresy obu funkcji są styczne.
Podobnie z równania [math]f_2(x)=g(x)\, [/math] mamy [math]\sin x=-1\, [/math] i ponownie punkty wspólne możemy numerować zmienną [math]n\, [/math]. Tym razem mają one postać: [math]\displaystyle \tilde{x}_n=\frac{3\pi}{2}+2 n\pi[/math] i mamy:
Otrzymaliśmy identyczne wartości, więc krzywe są styczne.