Matematyka 1 OO/Całki oznaczone
Zadanie
[math]\displaystyle \int _{-\infty }^{\infty } f(x)\,{\rm d}x\qquad [/math] gdzie [math]\qquad f(x)=\left\lbrace \begin{array}{rr} 0 & x\lt -3 \\ -2 & -3\le x\lt 1 \\ 0 & 1\le x\lt 3 \\ 4 & 3\le x\lt 6 \\ 0 & x\gt 6 \end{array} \right. [/math]
[math]\begin{matrix}\int _{-\infty }^{\infty } f(x)\,{\rm d}x&&\!\!\!\!\!\!\!\!= \int _{-\infty }^{-3}0\,{\rm d}x+\int _{-3}^1(-2)\,{\rm d}x+\int _1^30\,{\rm d}x+\int _3^64\,{\rm d}x+\int _6^\infty 0\,{\rm d}x\\&&\!\!\!\!\!\!\!\!= -2\int _{-3}^1\,{\rm d}x+4\int _3^6\,{\rm d}x=-2x\Big |_{-3}^1 +4 x\Big |_3^6 \\&&\!\!\!\!\!\!\!\!=-2(1-(-3))+4(6-3)=-8+12=4 \end{matrix}[/math]
Zadanie
[math]\begin{matrix}&&\!\!\!\!\!\!\!\!\int _0^{\pi /2}e^x\cos {x}\,{\rm d}x= \left| \begin{array}{ll} v=\cos {x} & v^{\prime }=-\sin {x} \\ u^{\prime }=e^x & u=e^x \end{array} \right|=e^x\cos {x}\Big |_0^{\pi /2} -\int _0^{\pi /2}e^x(-\sin {x})\,{\rm d}x\\&&\!\!\!\!\!\!\!\!=e^x\cos {x}\Big |_0^{\pi /2} +\int _0^{\pi /2}e^x\sin {x}\,{\rm d}x= \left| \begin{array}{ll} p=\sin {x} & p^{\prime }=\cos {x} \\ q^{\prime }=e^x & q=e^x \end{array} \right| \\&&\!\!\!\!\!\!\!\!=e^x\cos {x}\Big |_0^{\pi /2}+e^x\sin {x}\Big |_0^{\pi /2} -\int _0^{\pi /2}e^x\cos {x}\,{\rm d}x\\&&\!\!\!\!\!\!\!\!=e^{\pi /2}\cos \left(\frac{\pi }{2}\right)-e^0\cos (0) +e^{\pi /2}\sin \left(\frac{\pi }{2}\right)-e^0\sin (0) -\int _0^{\pi /2}e^x\cos {x}\,{\rm d}x\\&&\!\!\!\!\!\!\!\!=0-1+e^{\pi /2}-\int _0^{\pi /2}e^x\cos {x}\,{\rm d}x=e^{\pi /2}-1-\int _0^{\pi /2}e^x\cos {x}\,{\rm d}x\end{matrix}[/math]
Porównując pierwsze i ostatnie wyrażenie w powyższym ciągu równości dostajemy końcowy wynik:
- [math] \int _0^{\pi /2}e^x\cos {x}\,{\rm d}x=\frac{e^{\pi /2}-1}{2} [/math]
[math]\displaystyle \int _0^{\pi }e^x\cos {x}\,{\rm d}x[/math]
Korzystając z rachunków przeprowadzonych w poprzednim zadaniu, dostajemy:
[math]\begin{matrix}\int _0^{\pi }e^x\cos {x}\,{\rm d}x&&\!\!\!\!\!\!\!\!= \left.\frac{1}{2} \left[e^x\left(\cos {x}+\sin {x}\right)\right]\right|_0^{\pi } =\frac{1}{2} e^\pi (\cos (\pi )+\sin (\pi ))-\frac{1}{2} e^0(\cos (0)+\sin (0)) \\&&\!\!\!\!\!\!\!\!=\frac{1}{2}(-e^\pi -1)=-\frac{1+e^\pi }{2} \end{matrix}[/math]
[math]\displaystyle \int _{\pi /2}^{\pi }e^x\cos {x}\,{\rm d}x:\quad [/math]
Zamiast liczyć od początku, można skorzystać z wyników dwóch poprzednich rozwiązań
- [math] \int _{\pi /2}^{\pi }e^x\cos {x}\,{\rm d}x=\int _{0}^{\pi }e^x\cos {x}\,{\rm d}x-\int _{0}^{\pi /2}e^x\cos {x}\,{\rm d}x=-\frac{e^\pi +1}{2}-\frac{e^{\pi /2}-1}{2} =-\frac{e^\pi +e^{\pi /2}}{2} [/math]
[math]\displaystyle \int _{-1}^{2}\sqrt{-x^2+x+2}\,{\rm d}x[/math]
Sprawdzamy, czy funkcja pod pierwiastkiem ma miejsca zerowe:
- [math] \Delta =1+8=9 \qquad \qquad x_1=\frac{-1-3}{-2}=2 \qquad \qquad x_1=\frac{-1+3}{-2}=-1 [/math]
Granice całkowania pokrywają się z miejscami zerowymi funkcji pod pierwiastkiem. Funkcja podcałkowa, w granicach całkowania, ma wartości rzeczywiste. W wyrażeniu pod pierwiastkiem wyodrębniamy pełny kwadrat, a następnie dokonujemy zamiany zmiennych:
[math]\begin{matrix}&&\!\!\!\!\!\!\!\!\int _{-1}^{2}\sqrt{-x^2+x+2}\,{\rm d}x= \int _{-1}^{2}\sqrt{-x^2+2\frac{1}{2}x-\frac{1}{4}+\frac{1}{4}+2}\,{\rm d}x= \int _{-1}^{2}\sqrt{-\left(x-\frac{1}{2}\right)^2+\frac{9}{4}}\,{\rm d}x\\&&\!\!\!\!\!\!\!\!= \int _{-1}^{2}\sqrt{\frac{9}{4}\left(1-\frac{4}{9}\left(x-\frac{1}{2}\right)^2\right)}\,{\rm d}x= \int _{-1}^{2}\frac{3}{2}\sqrt{1-\left(\frac{2(x-\frac{1}{2})}{3}\right)^2}\,{\rm d}x\\&&\!\!\!\!\!\!\!\!= \left| \begin{array}{ll} y=2(x-1/2)/3 & y_1=2(x_1-1/2)/3=2(-1-1/2)/3=-1 \\ dy=(2/3){\rm d}x & y_2=2(x_2-1/2)/3=2(2-1/2)/3=1 \end{array} \right| \\&&\!\!\!\!\!\!\!\!= \frac{3}{2}\int _{-1}^{1}\sqrt{1-y^2}\,\frac{3}{2}\,{\rm d}y= \left| \begin{array}{lll} y=\sin (z) & y_1=\sin (z_1) & z_1=\arcsin (-1)=-\pi /2 \\ dy=\cos (z){\rm d}z & y_2=\sin (z_2) & z_2=\arcsin (1)=\pi /2 \end{array} \right| \\&&\!\!\!\!\!\!\!\!= \frac{9}{4}\int _{-\pi /2}^{\pi /2}\sqrt{1-\sin ^2{z}}\cos {z}\,{\rm d}z=\frac{9}{4}\int _{-\pi /2}^{\pi /2}\cos ^2(z)\,{\rm d}z\\&&\!\!\!\!\!\!\!\!= \left.\frac{9}{4}\left[ \frac{1}{2}\left(z+\sin {z}\cos {z}\right)\right]\right|_{-\pi /2}^{\pi /2} \\&&\!\!\!\!\!\!\!\!= \frac{9}{8}\left[ \left(\frac{\pi }{2}+\sin {\frac{\pi }{2}}\cos {\frac{\pi }{2}}\right) -\left(-\frac{\pi }{2}+\sin {\left(-\frac{\pi }{2}\right)} \cos {\left(-\frac{\pi }{2}\right)}\right) \right] = \frac{9}{8}\left[\frac{\pi }{2}+\frac{\pi }{2}\right] =\frac{9}{8}\pi \end{matrix}[/math]
Zadanie
[math]\begin{matrix}\int _0^1\frac{\,{\rm d}x}{x^2+3x+4} &&\!\!\!\!\!\!\!\!= \int _0^1\frac{\,{\rm d}x}{x^2+2\cdot \frac{3}{2}x+\frac{9}{4}-\frac{9}{4}+4} = \int _0^1\frac{\,{\rm d}x}{\left(x+\frac{3}{2}\right)^2+\frac{7}{4}} \\&&\!\!\!\!\!\!\!\!= \int _0^1\frac{\,{\rm d}x}{\frac{7}{4}\left[1+\frac{4}{7}\left(x+\frac{3}{2}\right)^2\right]} = \frac{4}{7}\int _0^1\frac{\,{\rm d}x}{1+\left(\frac{2\left(x+3/2\right)}{\sqrt{7}}\right)^2} \\&&\!\!\!\!\!\!\!\!= \left| \begin{array}{ll} y=2(x+3/2)/\sqrt{7} & y_1=2(0+3/2)/\sqrt{7}=3/\sqrt{7} \\ dy=(2/\sqrt{7})\,{\rm d}x & y_1=2(1+3/2)/\sqrt{7}=5/\sqrt{7} \end{array} \right| \\&&\!\!\!\!\!\!\!\!= \frac{4}{7}\int _{3/\sqrt{7}}^{5/\sqrt{7}}\frac{(\sqrt{7}/2)\,{\rm d}y}{1+y^2} = \frac{2}{\sqrt{7}}\int _{3/\sqrt{7}}^{5/\sqrt{7}}\frac{\,{\rm d}y}{1+y^2} =\left.\frac{2}{\sqrt{7}}\arctan {y}\right|_{3/\sqrt{7}}^{5/\sqrt{7}} \\&&\!\!\!\!\!\!\!\!=\frac{2}{\sqrt{7}} \left(\arctan {\frac{5}{\sqrt{7}}}-\arctan {\frac{3}{\sqrt{7}}}\right) \end{matrix}[/math]
Zadanie
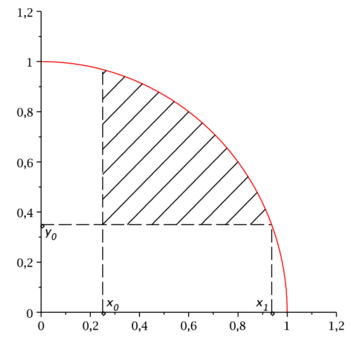
Obliczyć powierzchnię wycinka koła o promieniu jednostkowym ograniczonego warunkami: [math]x\gt x_0[/math], [math]y\gt y_0[/math], dla [math]0\lt x_0\lt 1[/math], [math]0\lt y_0\lt 1[/math].
Powierzchnia między wykresami dwóch funkcji [math]y=d(x)[/math] i [math]y=g(x)[/math] jest równa całce z różnicy [math]g(x)-d(x)[/math] w odpowiednich granicach.
W naszym przypadku: [math]g(x)[/math] jest równaniem okręgu; [math]d(x)=y_0[/math], a całkowanie należy wykonać po [math]x[/math] w granicach od [math]x_0[/math] do [math]x_1=\sqrt{1-y_0^2}[/math]
[math]\begin{matrix}&&\!\!\!\!\!\!\!\!P
=
\int _{x_0}^{x_1}\left(\sqrt{1-x^2}-y_0\right)\,{\rm d}x=
\int _{x_0}^{\sqrt{1-y_0^2}}\left(\sqrt{1-x^2}-y_0\right)\,{\rm d}x\\&&\!\!\!\!\!\!\!\!=
\int _{x_0}^{\sqrt{1-y_0^2}}\sqrt{1-x^2}\,{\rm d}x-y_0\int _{x_0}^{\sqrt{1-y_0^2}}\,{\rm d}x=
\int _{x_0}^{\sqrt{1-y_0^2}}\sqrt{1-x^2}\,{\rm d}x-y_0x\Big |_{x_0}^{\sqrt{1-y_0^2}}
\\&&\!\!\!\!\!\!\!\!=-y_0x\Big |_{x_0}^{\sqrt{1-y_0^2}}+\int _{x_0}^{\sqrt{1-y_0^2}}\sqrt{1-x^2}\,{\rm d}x=
\left|
\begin{array}{ll}
x=\sin {t} & x_0=\sin {t_0}
\\
{\rm d}x=\cos {t}\,{\rm d}t & x_1=\sin {t_1}
\end{array}
\right|
\\&&\!\!\!\!\!\!\!\!=-y_0x\Big |_{x_0}^{\sqrt{1-y_0^2}}
+\int _{t_0}^{t_1}\sqrt{1-\sin ^2{t}}\cos {t}\,{\rm d}t=-y_0x\Big |_{x_0}^{\sqrt{1-y_0^2}}
+\int _{t_0}^{t_1}\cos ^2{t}\,{\rm d}t\\&&\!\!\!\!\!\!\!\!=-y_0x\Big |_{x_0}^{\sqrt{1-y_0^2}}
+\left.\frac{1}{2}\left[t+\sin {t}\cos {t}\right]\right|_{t_0}^{t_1}
\\&&\!\!\!\!\!\!\!\!=-y_0x\Big |_{x_0}^{\sqrt{1-y_0^2}}
+\left.\frac{1}{2}\left[\arcsin {x}+x\sqrt{1-x^2}\right]
\right|_{x_0}^{x_1=\sqrt{1-y_0^2}}
\\&&\!\!\!\!\!\!\!\!=
-y_0\sqrt{1-y_0^2}+y_0x_0
+\frac{1}{2}\arcsin {\sqrt{1-y_0^2}}+\frac{1}{2}{\sqrt{1-y_0^2}}\,y_0
-\frac{1}{2}\arcsin {x_0}
\\&&\!\!
-\frac{1}{2}x_0\sqrt{1-x_0^2}
\\&&\!\!\!\!\!\!\!\!=\frac{1}{2}\arcsin {\sqrt{1-y_0^2}}-\frac{1}{2}\arcsin {x_0}
-\frac{1}{2}y_0{\sqrt{1-y_0^2}}-\frac{1}{2}x_0\sqrt{1-x_0^2}+x_0y_0
\end{matrix}[/math]
Ostatnie wyrażenie jest szukaną powierzchnią wycinka koła:
- [math] P=\frac{1}{2}\arcsin {\sqrt{1-y_0^2}}-\frac{1}{2}\arcsin {x_0} -\frac{1}{2}y_0{\sqrt{1-y_0^2}}-\frac{1}{2}x_0\sqrt{1-x_0^2}+x_0y_0 [/math]
Rozważmy przypadek szczególny: [math]x_0=y_0=0[/math]. W takim przypadku, ostatnie wyrażenie w powyższym ciągu równości daje:
- [math] P=\int _0^1\sqrt{1-x^2}\,{\rm d}x=\frac{1}{2}\arcsin (1)-0-0-0+0=\frac{1}{2}\cdot \frac{\pi }{2}=\frac{\pi }{4} [/math]
co rzeczywiście jest 1/4 powierzchni koła o jednostkowym promieniu.