Matematyka 1 OO/Funkcje elementarne jednej zmiennej rzeczywistej
Zadanie
Należy zacząć od sprawdzenia, co studenci pamiętają ze szkoły średniej na temat funkcji jednej zmiennej. Na początek można narysować kilka krzywych na tle układu współrzędnych (funkcja gładka, funkcja ciągła, funkcja nieciągła, i kilka krzywych nie będących wykresami funkcji) i urządzić quiz polegający na odgadywaniu, które krzywe są, a które nie są, wykresami funkcji.
Zadanie
Następnie przypominamy (dla części studentów wprowadzamy) podstawowe pojęcia opisujące funkcje na poziomie rysunków i objaśnień.
- Dziedzina.
- Miejsca zerowe.
- Ekstrema.
- Pochodna funkcji w punkcie jako tangens kąta między styczną do wykresu a osią [math]x[/math].
- Druga pochodna w punkcie jako pochodna pierwszej pochodnej. Druga pochodna jest dodatnia (ujemna), gdy pierwsza pochodna rośnie (maleje).
- Wypukłość i wklęsłość funkcji dla pewnego zakresu argumentu funkcji jako odpowiednia relacja między wartością rozpatrywanej funkcji i wartością funkcji liniowej przecinającej wykres badanej funkcji w punktach będących granicami zadanego zakresu argumentu.
- Wypukłość i wklęsłość funkcji jest związana także z zachowaniem wykresu funkcji w stosunku do stycznej do wykresu w danym punkcie. Wykres funkcja wypukłej (wklęsłej) w otoczeniu zadanego punktu leży powyżej (poniżej) stycznej.
- Punkty przegięcia mają tę własność, że wykres funkcji przecina styczną - po jednej stronie badanego punktu wykres funkcji leży powyżej, a po drugiej stronie poniżej prostej stycznej.
Zadanie
Formalizujemy warunek na wypukłość funkcji. Rysujemy układ współrzędnych oraz wykres jakiejś funkcji wypukłej i prostą przecinającą ten wykres w dwóch punktach.
Wykres funkcji liniowej [math]g(x)[/math] przecina wykres badanej funkcji [math]f(x)[/math] w dwóch punktach o współrzędnych [math](x_1,f(x_1))[/math] i [math](x_2,f(x_2))[/math]. To pozwala nam wyliczyć współczynniki [math]a[/math] i [math]b[/math]:
- [math] \left\lbrace \begin{array}{l} f(x_1)=ax_1+b\\ f(x_2)=ax_2+b \end{array} \right. [/math]
- [math] f(x_2)-f(x_1)=ax_2-ax_1=a(x_2-x_1) [/math]
- [math] a=\frac{f(x_2)-f(x_1)}{x_2-x_1} [/math]
- [math] b=f(x_1)-ax_1 = f(x_1)-x_1\frac{f(x_2)-f(x_1)}{x_2-x_1} = \frac{x_2f(x_1)-x_1f(x_2)}{x_2-x_1} [/math]
Tak więc funkcja liniowa [math]g(x)[/math] ma postać
- [math] g(x) = x \,\frac{f(x_2)-f(x_1)}{x_2-x_1} + \frac{x_2f(x_1)-x_1f(x_2)}{x_2-x_1} = \frac{(x-x_1)f(x_2)-(x-x_2)f(x_1)}{x_2-x_1} [/math]
Funkcja [math]f(x)[/math] jest wypukła w przedziale [math](x_1,x_2)[/math] jeśli
- [math] \begin{array}{ccc} f(x_3)\le g(x_3)\qquad & \mathrm{dla kazdego} & \qquad x_3\in (x_1,x_2) \end{array} [/math]
Punkty z przedziału [math](x_1,x_2)[/math] możemy sparametryzować jednym parametrem [math]\lambda [/math] z przedziału [math](0,1)[/math]:
- [math] x_3 = x_1 + \lambda (x_2-x_1) = \lambda x_2 + (1-\lambda ) x_1 [/math]
Taką postać [math]x_3[/math] podstawiamy do nierówności [math]f(x_3)\le g(x_3)[/math]:
[math]\begin{matrix} f\left(\lambda x_2 + (1-\lambda ) x_1\right) &&\!\!\!\!\!\!\!\! \le g\left(\lambda x_2 + (1-\lambda ) x_1\right) \\[4pt] &&\!\!\!\!\!\!\!\! = \frac{(x_1 + \lambda (x_2-x_1)-x_1)f(x_2) -(x_1 + \lambda (x_2-x_1)-x_2)f(x_1)}{x_2-x_1} \\ &&\!\!\!\!\!\!\!\! = \frac{\lambda (x_2-x_1)f(x_2) + (1-\lambda ) (x_2-x_1)f(x_1)}{x_2-x_1} \\ &&\!\!\!\!\!\!\!\! = \lambda f(x_2) + (1-\lambda ) f(x_1) \end{matrix}[/math]
Dla funkcji wypukłej wartość funkcji dla kombinacji liniowej dwóch argumentów jest nie większa niż odpowiednia kombinacja liniowa wartości funkcji dla każdego z tych argumentów:
- [math] f\big (\lambda x_2 + (1-\lambda ) x_1\big ) \le \lambda f(x_2) + (1-\lambda ) f(x_1) [/math]
Jeśli zamiast nierówności nieostrej mamy w powyższej relacji nierówność ostrą, funkcja jest ściśle wypukła.
Zadanie
Przypominamy definicje funkcji trygonometrycznych.
-
podajemy definicje
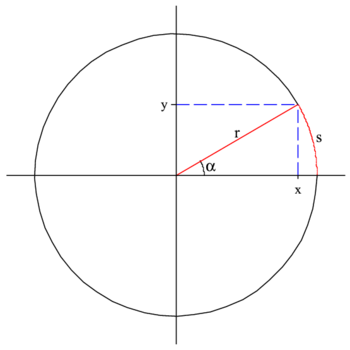
- [math] {\color {green}\cos (\alpha )=\frac{x}{r}} [/math]
- [math] {\color {red}\sin (\alpha )=\frac{y}{r}} [/math]
- [math] {\color {yellow}\tan (\alpha )=\frac{y}{x}} [/math]
- [math] {\color {blue}\cot (\alpha )=\frac{x}{y}} [/math]
-
Przypominamy definicję radianów:
- [math] \alpha =\frac{s}{r} [/math]
-
Rysujemy wykresy:
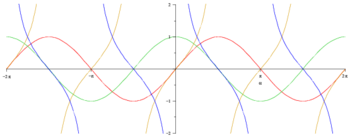 Przypominamy, że funkcja [math]\cos [/math] jest parzysta, a funkcje
[math]\sin [/math], [math]\tan [/math] i [math]\cot [/math] są nieparzyste.
Zwracamy uwagę na istnienie biegunów funkcji [math]\tan [/math] i [math]\cot [/math].
Przypominamy, że funkcja [math]\cos [/math] jest parzysta, a funkcje
[math]\sin [/math], [math]\tan [/math] i [math]\cot [/math] są nieparzyste.
Zwracamy uwagę na istnienie biegunów funkcji [math]\tan [/math] i [math]\cot [/math].
-
podajemy wartości dla kilku wybranych argumentów
[math]\alpha [/math] [math]\sin (\alpha )[/math] [math]\cos (\alpha )[/math] [math]\tan (\alpha )[/math] [math]\cot (\alpha )[/math] 0 0 1 0 – [math]\frac{\pi }{6}[/math] [math]\frac{1}{2}[/math] [math]\frac{\sqrt{3}}{2}[/math] [math]\frac{\sqrt{3}}{3}[/math] [math]\sqrt{3}[/math] [math]\frac{\pi }{4}[/math] [math]\frac{\sqrt{2}}{2}[/math] [math]\frac{\sqrt{2}}{2}[/math] [math]1[/math] [math]1[/math] [math]\frac{\pi }{3}[/math] [math]\frac{\sqrt{3}}{2}[/math] [math]\frac{1}{2}[/math] [math]\sqrt{3}[/math] [math]\frac{\sqrt{3}}{3}[/math] [math]\frac{\pi }{2}[/math] 1 0 – 0
-
Znając wartości funkcji trygonometrycznych dla argumentów z
przedziału [math](0,\pi )[/math] możemy obliczyć wartości dla dowolnych
innych argumentów korzystając ze wzorów
- [math] \begin{array}{ll} \sin \left(\alpha +\frac{\pi }{2}\right) = \cos (\alpha )\qquad & \qquad \cos \left(\alpha +\frac{\pi }{2}\right) = -\sin (\alpha ) \\[4pt] \tan \left(\alpha +\frac{\pi }{2}\right) = -\cot (\alpha )\qquad & \qquad \cot \left(\alpha +\frac{\pi }{2}\right) = -\tan (\alpha ) \end{array} [/math]
- [math] \left|x_{\alpha +\pi /2}\right|=\left|y_{\alpha }\right|\qquad \qquad \left|y_{\alpha +\pi /2}\right|=\left|x_{\alpha }\right| [/math]
- [math] \begin{array}{ll} \left|\sin \left(\alpha +\frac{\pi }{2}\right)\right| = \left|\cos (\alpha )\right|\qquad & \qquad \left|\cos \left(\alpha +\frac{\pi }{2}\right)\right| = \left|\sin (\alpha )\right| \\[4pt] \left|\tan \left(\alpha +\frac{\pi }{2}\right)\right| = \left|\cot (\alpha )\right|\qquad & \qquad \left|\cot \left(\alpha +\frac{\pi }{2}\right)\right| = \left|\tan (\alpha )\right| \end{array} [/math]
- [math] x_{\alpha +\pi /2}=-y_{\alpha } \qquad \qquad y_{\alpha +\pi /2}=+x_{\alpha } [/math]
-
Podajemy wzory na funkcje trygonometryczne od sumy argumentów
i wzór na “jedynkę trygonometryczną”:
- [math] \sin (\alpha \pm \beta ) = \sin (\alpha )\cos (\beta ) \pm \sin (\beta )\cos (\alpha ) [/math]
- [math] \cos (\alpha \pm \beta ) = \cos (\alpha )\cos (\beta ) \mp \sin (\beta )\sin (\alpha ) [/math]
- [math] \sin (\alpha )^2+\cos (\alpha )^2=1 [/math]
- [math] \cos (2\alpha )=\cos (\alpha +\alpha )=\cos ^2(\alpha )-\sin ^2(\alpha ) = 1-2\sin ^2(\alpha ) [/math]
- [math] \sin ^2(\alpha )=\frac{1}{2}\left(1-\cos (2\alpha )\right) [/math]
- [math] \sin (\alpha )=\pm \sqrt{\frac{1}{2}\left(1-\cos (2\alpha )\right)} [/math]
- [math] \sin \left(\frac{\pi }{8}\right) = \frac{\sqrt{2-\sqrt{2}}}{2} [/math]
Zadanie
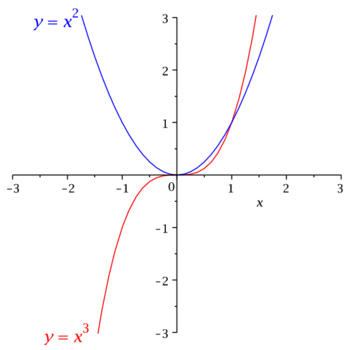
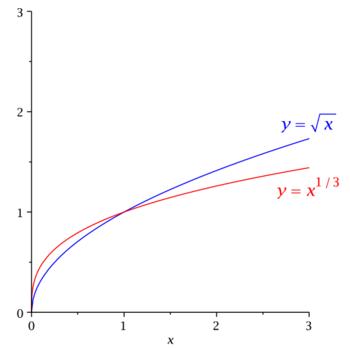
Przypominamy funkcje potęgowe.
Szkicujemy wykresy kilku takich funkcji, np.:
Zwracamy uwagę, że styczne do wykresów funkcji [math]y=x^c[/math] w punkcie [math]x=0[/math]
są poziome (pionowe) dla [math]c\gt 1[/math] ([math]c\lt 1[/math]).
Funkcja [math]y=x^c[/math] jest odwrotna do funkcji [math]x=y^{1/c}[/math], więc wykresy funkcji [math]y=x^c[/math] i [math]y=x^{1/c}[/math] są wzajemnie symetryczne przy odbiciu względem prostej [math]y=x[/math].
Może trzeba przypomnieć, co to jest funkcja odwrotna:
- [math] y=f(x) \qquad \Leftrightarrow \qquad x=f^{-1}(y) [/math]
Trzeba odróżniać funkcję odwrotną od odwrotności wartości funkcji, w ogólności
- [math] f^{-1}(x) \ne \frac{1}{f(x)} [/math]
UWAGA: jest tu pewna, dość powszechna, niekonsekwencja.
Jeśli [math]f^{-1}(x)[/math] oznacza wartość funkcji odwrotnej do [math]f[/math] dla argumentu
równego [math]x[/math], to przez [math]\sin ^2(x)[/math] powinniśmy rozumieć raczej złożenie
dwóch funkcji sinus a nie kwadrat wartości zwykłej funkcji sinus
dla argumentu równego [math]x[/math]. Puryści matematyczni powinni używać
[math](f^{-1})(x)[/math] na oznaczenie wartości funkcji odwrotnej. Tak czy inaczej,
warto studentom zwrócić uwagę na ten problem z notacją i umówić się
na stosowanie jakiejś konwencji.
Zadanie
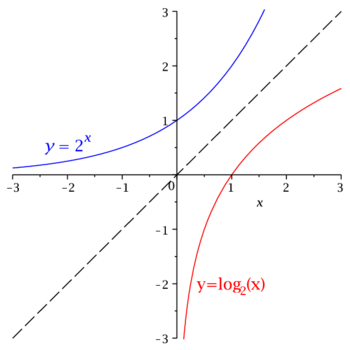
Przypominamy funkcje wykładnicze i logarytmiczne
- [math] y=\log _a(x) \qquad \Leftrightarrow \qquad x=a^y [/math]
Szkicujemy wykresy obu funkcji. Zwracamy uwagę, że wykres funkcji odwrotnej otrzymuje się przez odbicie względem prostej [math]y=x[/math] (w funkcji odwrotnej zmienna niezależna i zależna zamieniają się rolami).
Obliczamy wartości funkcji logarytmicznych w kilka prostych
przypadkach, np.:
- [math] \log _2(8)=3 \qquad \log _2(128)=7 \qquad \log _2(1024)=10 \qquad \log _3(81)=4 [/math]
Wyprowadzamy wzory:
- [math] \log _a(x\cdot y) = \log _a(x) + \log _a(y) [/math]
- [math] \log _a(x^n) = n \log _a(x) [/math]
Przy ich pomocy pokazujemy np.:
- [math] \log _a\left(\frac{1}{x}\right)=-\log _a(x) [/math]
Przy okazji warto przypomnieć relację
- [math] x^{-c}=\frac{1}{x^c} [/math]
To może się wydawać bardzo elementarna wiedza, ale niestety wielu absolwentów szkół średnich jej nie posiada.
Zadanie
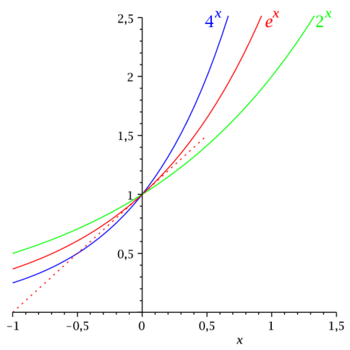
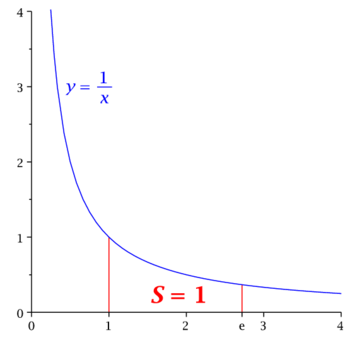
Wprowadzamy liczbę [math]e[/math]. Związki z granicą ciągu [math](1+1/n)^n[/math] i sumą szeregu [math]\sum _{k=1}^\infty 1/(k!)[/math] pojawią się później. Teraz możemy podać np. dwie następujące własności liczby [math]e[/math]:
- Pole powierzchni pod wykresem funkcji [math]y=1/x[/math] między [math]x=1[/math] a [math]x=e[/math] jest równe 1.
- Styczna do wykresu funkcji wykładniczej [math]y=a^x[/math] w punkcie [math]x=0[/math] ma kąt nachylenia równy [math]\pi /4[/math], tylko wtedy gdy [math]a=e[/math].
Oczywiście należy podać kilka pierwszych liczb rozwinięcia dziesiętnego
liczby [math]e[/math], podkreślając, że jest to liczba niewymierna
- [math] e=2.718281828459\ldots [/math]
Zadanie
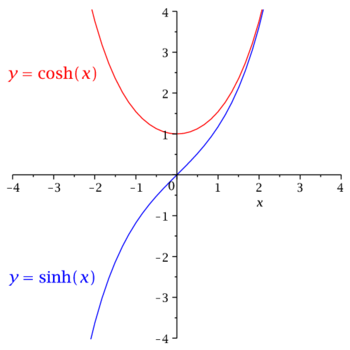
Wprowadzamy funkcje hiperboliczne. Podajemy definicje
- [math] \cosh {x}=\frac{e^x+e^{-x}}{2} [/math]
- [math] \sinh {x}=\frac{e^x-e^{-x}}{2} [/math]
Szkicujemy wykresy
i zwracamy uwagę na (nie)parzystość tych funkcji oraz
na bardzo podobne wartości obu funkcji dla dużych
argumentów.
Prezentujemy “jedynkę hiperboliczną”:
[math]\begin{matrix} \cosh ^2(x)-\sinh ^2(x) &&\!\!\!\!\!\!\!\! = \left(\frac{e^x+e^{-x}}{2}\right)^2 - \left(\frac{e^x-e^{-x}}{2}\right)^2 \\[4pt] &&\!\!\!\!\!\!\!\! = \frac{e^{2x}+2+e^{-2x}-\left(e^{2x}-2+e^{-2x}\right)}{4} = \frac{4}{4}=1 \end{matrix}[/math]
Robimy analogiczne obliczenia dla znaku “[math]+[/math]”:
[math]\begin{matrix} \cosh ^2(x)+\sinh ^2(x) &&\!\!\!\!\!\!\!\! = \left(\frac{e^x+e^{-x}}{2}\right)^2 + \left(\frac{e^x-e^{-x}}{2}\right)^2 \\[4pt] &&\!\!\!\!\!\!\!\! = \frac{e^{2x}+2+e^{-2x}+\left(e^{2x}-2+e^{-2x}\right)}{4} = \frac{2e^{2x}+2e^{-2x}}{4} = \cosh (2x) \end{matrix}[/math]
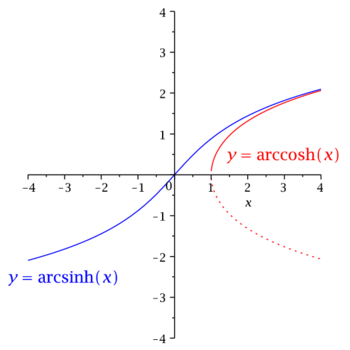
Znajdujemy funkcję odwrotną do funkcji [math]\cosh [/math]:
- [math] y=(\cosh ^{-1})(x)={\rm arccosh}(x) [/math]
- [math] x=\cosh (y)=\frac{e^y+e^{-y}}{2} [/math]
- [math] 2x=e^y+e^{-y} \qquad ||\cdot e^y [/math]
- [math] e^{2y}-2xe^{y}+1=0 [/math]
Wprowadzamy nową zmienną [math]z=e^y[/math] i dostajemy równanie kwadratowe
- [math] z^2-2xz+1=0 [/math]
które rozwiązujemy tradycyjną metodą
- [math] \Delta =(2x)^2-4=4x^2-4=4(x^2-1) [/math]
- [math] z_{1,2}=\frac{2x\pm \sqrt{\Delta }}{2} = \frac{2x\pm \sqrt{4(x^2-1)}}{2} = x\pm \sqrt{x^2-1} [/math]
Powracamy do zmiennej [math]y[/math]
- [math] y=\ln (z)=\ln \left(x\pm \sqrt{x^2-1}\right) [/math]
Rozwiązanie nie jest jednoznaczne, są dwa możliwe znaki przed pierwiastkiem. Powód jest następujący: funkcja odwrotna odpowiada zamianie rolami zmiennych [math]x[/math] i [math]y[/math]. Na wykresie odpowiada to odbiciu względem prostej [math]y=x[/math]. Takie odbicie wykresu funkcji [math]\cosh (x)[/math] nie jest już wykresem funkcji. W definicji funkcji odwrotnej, [math](\cosh ^{-1})(x)[/math], musimy się zdecydować na jedną z możliwych gałęzi. Jest to sprawa konwencji (sytuacja podobna do funkcji pierwiastkowej, która jest funkcją odwrotną do funkcji kwadratowej - umawiamy się, że pierwiastki liczb dodatnich są dodatnie).
Podobnych problemów nie ma w przypadku funkcji [math]{\rm arcsinh}(x)[/math]. Jej obliczenie możemy zadać do samodzielnego wykonania w domu.
Z wykresu widać, że dwie możliwe gałęzie funkcji [math]{\rm arccosh}(x)[/math]
różnią się tylko znakiem. Sprawdzamy, czy to samo wynika z
uzyskanych wcześniej wzorów:
[math]\begin{matrix} -\ln \left(x+\sqrt{x^2-1}\right) &&\!\!\!\!\!\!\!\! = \ln \left(\frac{1}{x+\sqrt{x^2-1}}\right) = \ln \left(\frac{1}{x+\sqrt{x^2-1}}\cdot \frac{x-\sqrt{x^2-1}}{x-\sqrt{x^2-1}}\right) \\ &&\!\!\!\!\!\!\!\! = \ln \left(\frac{x-\sqrt{x^2-1}}{(x-\sqrt{x^2-1})(x-\sqrt{x^2-1})}\right) = \ln \left(\frac{x-\sqrt{x^2-1}}{x^2-(x^2-1)}\right) \\ &&\!\!\!\!\!\!\!\! = \ln \left(x-\sqrt{x^2-1}\right) \end{matrix}[/math]
Rzeczywiście, obydwie znalezione przez nas funkcje odwrotne do [math]\cosh (x)[/math] różnią się tylko znakiem.
Zadanie
Składanie funkcji.
Dwie funkcje można złożyć na dwa sposoby, różniące się tym, która funkcja jest funkcją wewnętrzną, a która zewnętrzną. Dyskutujemy dwa przykłady.
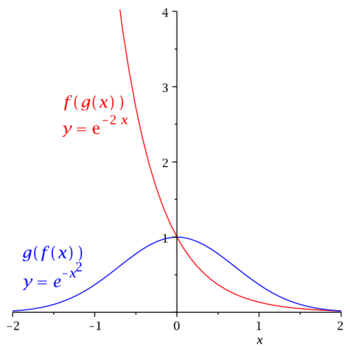
[math]f(x)=x^2[/math], [math]\quad g(x)=e^{-x} [/math]
- [math] {\color {blue}g(f(x))=e^{-f(x)}=e^{-x^2}} [/math]
- [math] {\color {red}f(g(x))=(g(x))^2=\left(e^{-x}\right)^2=e^{-2x}} [/math]
Wykresy tych funkcji są zupełnie różne i nie ma między nimi tak prostej relacji jak między wykresami zadanej funkcji i funkcji do niej odwrotnej
Zadanie
- [math] f(x)=\sin (x) \qquad \qquad g(x)=\sqrt{1-x^2} [/math]
- [math] {\color {blue} g(f(x))=\sqrt{1-[f(x)]^2} = \sqrt{1-\sin ^2(x)} = \sqrt{\cos ^2(x)} = |\cos (x)| } [/math]
- [math] {\color {red} f(g(x))=\sin \left(g(x)\right) = \sin \left(\sqrt{1-x^2}\right) } [/math]
Dziedziną tej ostatniej funkcji jest zbiór domknięty [math][-1,1][/math].