Matematyka 1 OO/Zderzenia
Zadanie
Zderzenie centralne idealnie niesprężyste (ciała zlepiają się i po zderzeniu poruszają się razem). Jedno z ciał przed zderzeniem jest w spoczynku.
Oczywiście masa sklejonych ciał jest sumą poszczególnych mas
- [math] m_{12}=m_1+m_2 [/math]
Zasada zachowania pędu:
- [math] m_1 \vec{v}_0+m_2\vec{0}=m_{12}\vec{v}_{12}=(m_1+m_2)\vec{v}_{12} [/math]
pozwala obliczyć prędkość po zderzeniu
- [math] \vec{v}_{12}=\frac{m_1}{m_1+m_2}\vec{v}_0 [/math]
Sprawdzamy, czy w takim zderzeniu zachowana jest energia kinetyczna:
- [math] E_0 = \frac{1}{2} m_1 |\vec{v}_0|^2 [/math]
[math]\begin{matrix} E_{12} &&\!\!\!\!\!\!\!\! = \frac{1}{2} m_{12} |\vec{v}_{12}|^2 = \frac{1}{2} (m_1+m_2)\frac{m_1^2}{(m_1+m_2)^2} |\vec{v}_0|^2 \\&&\!\!\!\!\!\!\!\! =\frac{1}{2} \frac{m_1^2}{m_1+m_2} |\vec{v}_0|^2 =\frac{m_1}{m_1+m_2}\cdot \frac{1}{2} m_1 |\vec{v}_0|^2 =\frac{m_1}{m_1+m_2}E_0 \end{matrix}[/math]
Obie masy [math]m_1[/math] i [math]m_2[/math] są dodatnie, więc [math]E_{12}\lt E_0[/math].
W czasie zderzenia niesprężystego, część energii kinetycznej
zamienia się na energię wewnętrzną ciał biorących w nim udział.
Zadanie
Zderzenie centralne, idealnie sprężyste (energia kinetyczna jest zachowana) dwóch kul. Jedna z kul przed zderzeniem jest w spoczynku.
Zasady zachowania pędu i zachowania energii kinetycznej
- [math] \left\lbrace \begin{array}{l} m_1 \vec{v}_0 = m_1 \vec{v}_1 + m_2 \vec{v}_2 \\[4pt] \displaystyle \frac{1}{2} m_1 \vec{v}_0^{\,2} = \frac{1}{2} m_1 \vec{v}_1^{\,2} + \frac{1}{2} m_2 \vec{v}_2^{\,2} \end{array} \right. [/math]
Z zasady zachowania pędu wyznaczmy [math]v_2[/math]
- [math] \vec{v}_2 = \frac{m_1}{m_2}\left(\vec{v}_0-\vec{v}_1\right) [/math]
i podstawiamy do równania opisującego zachowanie energii kinetycznej (pomnożonego przez 2):
- [math] m_1 \vec{v}_0^{\,2} = m_1 \vec{v}_1^{\,2} + m_2\, \frac{m_1^2}{m_2^2}\left(\vec{v}_0-\vec{v}_1\right)^2 [/math]
- [math] m_1 \vec{v}_0^{\,2} = m_1 \vec{v}_1^{\,2} + \frac{m_1^2}{m_2}\left( \vec{v}_0^{\,2}-2\vec{v}_0\cdot \vec{v}_1+\vec{v}_1^{\,2}\right) [/math]
Zderzenie jest centralne, więc wszystkie prędkości mają jeden kierunek (choć może nie koniecznie ten sam zwrot).
- [math] \vec{v}_0\parallel \vec{v}_1 \qquad \Rightarrow \qquad \vec{v}_0\cdot \vec{v}_1=|\vec{v}_0|\cdot |\vec{v}_1| =v_0v_1 [/math]
gdzie [math]v_i\equiv |\vec{v}_i|[/math]. Przekształcamy dalej wzór opisujący zasadę zachowania energii kinetycznej:
- [math] m_1 {v}_0^{\,2} = m_1 {v}_1^{\,2} + \frac{m_1^2}{m_2}\left({v}_0^{\,2}-2{v}_0{v}_1+{v}_1^{\,2}\right) [/math]
- [math] 0 = {v}_1^{\,2} \left[m_1\left(1+\frac{m_1}{m_2}\right)\right] - {v}_1\cdot 2 \frac{m_1^2}{m_2}{v}_0 + m_1\left(\frac{m_1}{m_2}-1\right) {v}_0^{\,2} [/math]
Jest to równanie kwadratowe na wielkość skalarną [math]{v}_1[/math]. Rozwiązujemy je
- [math] \Delta = 4\frac{m_1^4}{m_2^2} {v}_0^{\,2} - 4 m_1^2 \left(1+\frac{m_1}{m_2}\right)\left(\frac{m_1}{m_2}-1\right) {v}_0^{\,2} = 4 {v}_0^{\,2}m_1^2 \left[\frac{m_1^2}{m_2^2}+1-\frac{m_1^2}{m_2^2}\right] = 4 m_1^2 {v}_0^{\,2} [/math]
- [math] v_1 = \frac{2\displaystyle \frac{m_1^2}{m_2}v_0 \pm 2m_1v_0}{2m_1\left(1+\displaystyle \frac{m_1}{m_2}\right)} = \frac{2m_1v_0\left(\displaystyle \frac{m_1}{m_2}\pm 1\right)}{2m_1\left(1+\displaystyle \frac{m_1}{m_2}\right)} = v_0\frac{\left(\displaystyle \frac{m_1}{m_2}\pm 1\right)}{\left(1+\displaystyle \frac{m_1}{m_2}\right)} = v_0\frac{m_1 \pm m_2}{m_1 + m_2} [/math]
Obliczone [math]v_1[/math] podstawiamy do wzoru na [math]v_2[/math]
- [math] v_2 = \frac{m_1}{m_2}\left(v_0 -v_1\right) = v_0\frac{m_1}{m_2}\left(1-\frac{m_1 \pm m_2}{m_1+m_2}\right) = v_0\frac{m_1}{m_2}\frac{(1\mp 1)m_2}{m_1+m_2} = v_0\frac{(1\mp 1)m_1}{m_1+m_2} [/math]
Należy zbadać, co oznacza istnienie dwóch różnych rozwiązań (kule po zderzeniu powinny przecież mieć dobrze określone prędkości). Upraszczamy każde z rozwiązań na [math]v_1[/math] i [math]v_2[/math]:
- [math] v_1^{(1)} = v_0\,\frac{m_1 + m_2}{m_1 + m_2} = v_0 \qquad \qquad v_2^{(1)} = 0 [/math]
Prędkości obu kul po zderzeniu są takie same jak przed zderzeniem: kula o masie [math]m_1[/math] porusza się z początkową prędkością [math]v_0[/math], a kula o masie [math]m_2[/math] pozostaje w spoczynku. To rozwiązanie opisuje sytuację, gdy do zderzenia nie doszło (brak zderzenia jest oczywiście zgodny z zasadami zachowania pędu i energii kinetycznej).
- [math] v_1^{(2)} = v_0\,\displaystyle \frac{m_1-m_2}{m_1+m_2} \qquad \qquad v_2^{(2)} = v_0\,\frac{2m_1}{m_1+m_2} [/math]
To rozwiązanie odpowiada sytuacji, gdy do zderzenia rzeczywiście doszło. Prędkość drugiego ciała jest zawsze dodatnia (czyli i kierunek i zwrot wektora prędkości [math]\vec{v}_2[/math] jest taki sam jak wektora [math]\vec{v}_0[/math]). Znak wartości prędkości [math]v_1[/math] zależy od mas zderzających się ciał. Jest on ujemny, jeśli pierwsze ciało jest lżejsze od drugiego. W takiej sytuacji pierwsze ciało odbija się od drugiego i porusza się w kierunku przeciwnym do kierunku przez zderzeniem.
W przypadku równych mas [math]m_1[/math] i [math]m_2[/math] otrzymujemy:
- [math] v_1=0 \qquad \qquad v_2=v_0 [/math]
Pierwsze ciało zatrzymuje się i przekazuje całą energię kinetyczną drugiemu ciału, które zaczyna się poruszać z prędkością równą prędkości pierwszego ciała przed zderzeniem.
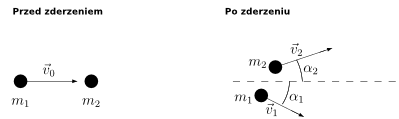
Zadanie
Zderzenie niecentralne niesprężyste
Wprowadzamy układ współrzędnych z osią [math]x[/math] skierowaną zgodnie z początkową prędkością [math]\vec{v}_0[/math]. Zasadę zachowania pędu
- [math] m_1\vec{v}_0 = m_1\vec{v}_1 + m_2 \vec{v}_2 [/math]
rozpisujemy na składowe
- [math] \left\lbrace \begin{array}{l} m_1 v_0 = m_1 v_1 \cos (\alpha _1) + m_2 v_2 \cos (\alpha _2) \\[4pt] 0 = m_1 v_1 \sin (-\alpha _1) + m_2 v_2 \sin (\alpha _2) \end{array} \right. [/math]
Są to 2 równania na 4 niewiadome: 4 składowe kartezjańskie dwóch prędkości ([math]v_{1x}[/math], [math]v_{1y}[/math], [math]v_{2x}[/math], [math]v_{2y}[/math]) lub dwie prędkości ([math]v_1[/math] i [math]v_2[/math]) i dwa kąty ([math]\alpha _1[/math] i [math]\alpha _2[/math]).
W ogólności układ dwóch równań na 4 niewiadome ma nieskończenie wiele rozwiązań. Możemy tylko wyznaczyć dwie niewiadome jako funkcje dwóch pozostałych niewiadomych.
Zadanie
Możemy wyznaczyć wartości prędkości w funkcji kątów:
Z [math]y[/math]-owej składowej zasady zachowania pędu dostajemy
- [math] v_2 = v_1\, \frac{m_1}{m_2}\,\frac{\sin (\alpha _1)}{\sin (\alpha _2)} [/math]
Podstawienie tego do [math]x[/math]-owej składowej zasady zachowania pędu daje
- [math] m_1 v_0 = m_1 v_1 \cos (\alpha _1) + m_2 v_1\, \frac{m_1}{m_2}\,\frac{\sin (\alpha _1)}{\sin (\alpha _2)}\cos (\alpha _2) [/math]
- [math] v_0 = v_1 \cos (\alpha _1) + v_1\, \frac{\sin (\alpha _1)}{\sin (\alpha _2)}\cos (\alpha _2) [/math]
- [math] v_0 \sin (\alpha _2) = v_1 \sin (\alpha _2)\cos (\alpha _1) + v_1 \sin (\alpha _1)\cos (\alpha _2) = v_1 \sin (\alpha _1+\alpha _2) [/math]
- [math] v_1 = v_0\,\frac{\sin (\alpha _2)}{\sin (\alpha _1+\alpha _2)} [/math]
Podstawienie tego [math]v_1[/math] do wzoru na [math]v_2[/math] daje
- [math] v_2 = v_1\, \frac{m_1}{m_2}\,\frac{\sin (\alpha _1)}{\sin (\alpha _2)} = \frac{m_1}{m_2}v_0\,\frac{\sin (\alpha _2)}{\sin (\alpha _1+\alpha _2)} \,\frac{\sin (\alpha _1)}{\sin (\alpha _2)} = v_0\,\frac{m_1}{m_2}\,\frac{\sin (\alpha _1)}{\sin (\alpha _1+\alpha _2)} [/math]
Zadanie
Możemy też wyznaczyć kąty w funkcji pędów:
Na początek przekształcamy obie składowe zasady zachowania pędu
- [math] \left\lbrace \begin{array}{l} \left(m_1 v_0 - m_1 v_1 \cos (\alpha _1)\right)^2 = m_2^2 v_2^2 \cos ^2(\alpha _2) \\[4pt] m_1^2 v_1^2 \sin ^2(\alpha _1) = m_2^2 v_2^2 \sin ^2(\alpha _2) \end{array} \right. [/math]
- [math] \left\lbrace \begin{array}{l} m_1^2 v_0^2 - 2 m_1^2 v_0 v_1 \cos (\alpha _1) + m_1^2 v_1^2 \cos ^2(\alpha _1) = m_2^2 v_2^2 \cos ^2(\alpha _2) \\[4pt] m_1^2 v_1^2 \sin ^2(\alpha _1) = m_2^2 v_2^2 \sin ^2(\alpha _2) \end{array} \right. [/math]
Dodając obie te równości stronami dostajemy
- [math] m_1^2 v_0^2 - 2 m_1^2 v_0 v_1 \cos (\alpha _1)+ m_1^2 v_1^2 = m_2^2 v_2^2 [/math]
co pozwala wyznaczyć cosinus kąta [math]\alpha _1[/math]
- [math] \cos (\alpha _1) = \frac{m_1^2 v_0^2+m_1^2 v_1^2 - m_2^2 v_2^2}{ 2 m_1^2 v_0 v_1} [/math]
Podstawiając ten wynik do [math]x[/math]-owej składowej zasady zachowania pędu obliczamy drugi kąt
- [math] m_2 v_2 \cos (\alpha _2)= m_1 v_0 - m_1 v_1 \frac{m_1^2 v_0^2+m_1^2 v_1^2 - m_2^2 v_2^2}{ 2 m_1^2 v_0 v_1} [/math]
- [math] \cos (\alpha _2) = \frac{m_1^2 v_0^2 - m_1^2 v_1^2 + m_2^2 v_2^2}{ 2 m_1 m_2 v_0 v_2} [/math]
Wzory na oba kąty wyrażają się dość prosto przez stosunek, w jakim początkowy pęd [math]p_0[/math] “dzieli się” między oba ciała
- [math] \cos (\alpha _1) = \frac{1+\xi _1-\xi _2}{2\xi _1} \qquad \qquad \cos (\alpha _2) = \frac{1+\xi _2-\xi _1}{2\xi _2} [/math]
gdzie dla [math]i=1,2[/math]
- [math] \xi _i=\frac{p_i}{p_0}=\frac{m_i v_i}{m_1 v_0} [/math]
Zadanie
Policzmy jeszcze zmianę energii kinetycznej w taki zderzeniu
- [math] \Delta E = E_0 - E_1 - E_2 = \frac{1}{2} m_1 v_0^2 - \frac{1}{2} m_1 v_1^2 - \frac{1}{2} m_2 v_2^2 [/math]
- [math] \frac{\Delta E}{E_0} = 1 - \frac{v_1^2}{v_0^2} - \frac{m_2}{m_1}\,\frac{v_2^2}{v_0^2} = 1 - \frac{\sin ^2(\alpha _2)}{\sin ^2(\alpha _1+\alpha _2)} - \frac{m_1}{m_2}\,\frac{\sin ^2(\alpha _1)}{\sin ^2(\alpha _1+\alpha _2)} [/math]
- [math] \frac{\Delta E}{E_0} = \frac{m_2 \sin ^2(\alpha _1+\alpha _2)-m_2 \sin ^2(\alpha _2) - m_1 \sin ^2(\alpha _1)}{m_2 \sin ^2(\alpha _1+\alpha _2)} [/math]
Zderzenie jest sprężyste, jeśli licznik powyższego wyrażenia znika. Jest to warunek łączący kąty rozpraszania [math]\alpha _1[/math] i [math]\alpha _2[/math]
- [math] m_2 \sin ^2(\alpha _1+\alpha _2) = m_2 \sin ^2(\alpha _2) + m_1 \sin ^2(\alpha _1) [/math]
Zadanie
Zderzenie niecentralne idealnie sprężyste
Rysunek jak do poprzedniego zadania. Zasada zachowania pędu (dwie składowe) i zasada zachowania energii tworzą układ 3 równań na cztery niewiadome
- [math] \left\lbrace \begin{array}{l} m_1 v_0 = m_1 v_1 \cos (\alpha _1) + m_2 v_2 \cos (\alpha _2) \\[4pt] 0 = m_1 v_1 \sin (-\alpha _1) + m_2 v_2 \sin (\alpha _2) \\[4pt] m_1 v_0^2 = m_1 v_1^2 + m_2 v_2^2 \end{array} \right. [/math]
Niewiadomych jest o jedną więcej niż równań, więc rozwiązania nie są jednoznaczne. Jeśli zadamy jedną z wielkości, np. jeden z kątów [math]\alpha _i[/math], to możemy wtedy obliczyć drugi kąt i wartości obu prędkości [math]v_{1,2}[/math]. Wynik znaleźliśmy już w zadaniu 9.3:
- [math] \left\lbrace \begin{array}{l} \displaystyle v_1=v_0\,\frac{\sin (\alpha _2)}{\sin (\alpha _1+\alpha _2)} \\[4pt] \displaystyle v_2=v_0\,\frac{m_1}{m_2}\,\frac{\sin (\alpha _1)}{\sin (\alpha _1+\alpha _2)} \\[6pt] \displaystyle \sin ^2(\alpha _1+\alpha _2) = \sin ^2(\alpha _2) + \frac{m_1}{m_2} \sin ^2(\alpha _1) \end{array} \right. [/math]
Nie jest on bardzo prosty w ogólnym przypadku, więc rozpatrzymy kilka prostych przykładów.
Zadanie
Równe masy [math]m_2=m_1[/math]
Zasada zachowania energii przybiera w tym przypadku postać
- [math] \sin ^2(\alpha _1+\alpha _2) = \sin ^2(\alpha _2) + \sin ^2(\alpha _1) [/math]
- [math] \left(\sin (\alpha _1)\cos (\alpha _2)+\sin (\alpha _2)\cos (\alpha _1)\right)^2 = \sin ^2(\alpha _2) + \sin ^2(\alpha _1) [/math]
[math]\begin{matrix} \sin ^2(\alpha _1)\cos ^2(\alpha _2) +2\sin (\alpha _1)\cos (\alpha _1)\sin (\alpha _2)\cos (\alpha _2) +\sin ^2(\alpha _2)\cos ^2(\alpha _1)= \qquad \qquad \\ = \sin ^2(\alpha _2) + \sin ^2(\alpha _1) \end{matrix}[/math]
- [math] \sin ^2(\alpha _1)[\cos ^2(\alpha _2)-1] +2\sin (\alpha _1)\cos (\alpha _1)\sin (\alpha _2)\cos (\alpha _2) +\sin ^2(\alpha _2)[\cos ^2(\alpha _1)-1] =0 [/math]
- [math] -2\sin ^2(\alpha _1)\sin ^2(\alpha _2) +2\sin (\alpha _1)\cos (\alpha _1)\sin (\alpha _2)\cos (\alpha _2) =0 [/math]
- [math] \sin ^2(\alpha _1)\sin ^2(\alpha _2) = \sin (\alpha _1)\cos (\alpha _1)\sin (\alpha _2)\cos (\alpha _2) [/math]
To równanie ma 3 rozwiązania
- [math] \sin (\alpha _1)=0 \qquad \vee \qquad \sin (\alpha _2)=0 \qquad \vee \qquad \sin (\alpha _1)\sin (\alpha _2)=\cos (\alpha _1)\cos (\alpha _2) [/math]
Rozpatrzmy je po kolei.
-
Jeśli [math]\sin (\alpha _1)=0[/math] to [math]\sin (\alpha _1+\alpha _2)=\sin (\alpha _2)[/math]
i wzory na wartości prędkości dają:
- [math] v_1=v_0 \qquad \qquad v_2=0 [/math]
-
Jeśli [math]\sin (\alpha _2)=0[/math] to [math]\sin (\alpha _1+\alpha _2)=\sin (\alpha _1)[/math]
i wzory na wartości prędkości dają:
- [math] v_1=0 \qquad \qquad v_2=v_0 [/math]
-
“Prawdziwie” niecentralne i sprężyste zderzenie opisuje
trzecie rozwiązanie
- [math] \cos (\alpha _1)\cos (\alpha _2)=\sin (\alpha _1)\sin (\alpha _2) [/math]
- [math] 0=\cos (\alpha _1)\cos (\alpha _2)-\sin (\alpha _1)\sin (\alpha _2) =\cos (\alpha _1+\alpha _2) [/math]
- [math] \alpha _1+\alpha _2=\frac{\pi }{2} [/math]
Ten ostatni wniosek można także udowodnić stosując metodę graficzną. Zasada zachowania pędu ma następującą postać wektorową
- [math] \vec{p}_0=\vec{p}_1+\vec{p}_2 [/math]
podczas gdy dla równych mas zasada zachowania energii kinetycznej to następujące równanie skalarne
- [math] p_0^2=p_1^2+p_2^2 [/math]
Równanie wektorowe mówi nam, że odcinki o długościach [math]p_0[/math], [math]p_1[/math] i [math]p_2[/math] tworzą trójkąt. W takim przypadku równanie skalarne jest równaniem Pitagorasa które jest słuszne, jeśli między bokami o długościach [math]p_1[/math] i [math]p_2[/math] jest kąt prosty.
Zadanie
Inny prosty przykład: [math]\alpha _1=\alpha _2=\alpha [/math]
(Oczywiście dla [math]m_1 \ne m_2[/math], bo w przypadku równych mas z warunku [math]\alpha _1+\alpha _2=\pi /2[/math] natychmiast dostalibyśmy rozwiązanie [math]\alpha _1=\alpha _2=\pi /4[/math])
Tym razem zasada zachowania energii kinetycznej daje
- [math] \sin ^2(2\alpha )=\sin ^2(\alpha )+\frac{m_1}{m_2}\sin (\alpha ) =\sin ^2(\alpha )\left(1+\frac{m_1}{m_2}\right) [/math]
Wyliczamy stąd cosinus kąta [math]\alpha [/math]
- [math] 1+\frac{m_1}{m_2} = \frac{\sin ^2(2\alpha )}{\sin ^2(\alpha )} = \frac{[2\sin (\alpha )\cos (\alpha )]^2}{\sin ^2(\alpha )} = 4\cos ^2(\alpha ) [/math]
- [math] \cos (\alpha )=\frac{1}{2}\,\sqrt{1+\frac{m_1}{m_2}} [/math]
Oczywiści [math]\cos ^2(\alpha )[/math] nie może być większy niż 1
- [math] 1\ge \cos ^2(\alpha )=\frac{1}{4}\left(1+\frac{m_1}{m_2}\right) [/math]
- [math] \frac{m_1}{m_2}\le 3 [/math]
Ciała nie mogą rozproszyć się symetrycznie ([math]\alpha _1=\alpha _2[/math]), jeśli ciało “pocisk” jest więcej niż trzykrotnie cięższe od ciała “tarczy”.
Z oczywistego warunku dodatniości masy pierwszego ciała otrzymujemy warunek na kąt rozpraszania [math]\alpha [/math]:
- [math] \cos ^2(\alpha )=\frac{1}{4}\left(1+\frac{m_1}{m_2}\right)\gt \frac{1}{4} [/math]
- [math] \cos (\alpha )\gt \frac{1}{2} \qquad \qquad \Rightarrow \qquad \qquad \alpha \lt \frac{\pi }{3} [/math]
Do kąta granicznego [math]\pi /3[/math] zbliżamy się, jeśli stosunek mas [math]m_1/m_2[/math] dąży do zera.