Metody hydrodynamiczne
Spis treści
Zadanie 1
Oblicz wartość przyspieszenia odśrodkowego (w jednostkach g) działającego na próbkę podczas eksperymentu ultrawirowania. Przyjmij, że rotor obraca się z maksymalną prędkością [math]\omega[/math] = 60 000 obrotów/min (rpm), a odległość kuwety pomiarowej od osi obrotu wynosi około [math]r = \unit{6,5}{ cm}[/math].
Zadanie 2
Wyprowadź zależność wiążącą masę molową M, współczynnik sedymentacji s i współczynnik dyfuzji D (równanie Svedberga).
Zadanie 3
Współczynnik dyfuzji 2% roztworu globularnego białka o masie cząsteczkowej [math]M = \unit{68}{ kDa}[/math] w temperaturze [math]T = \unit{20}{ ^oC}[/math] wynosi [math]D = \unit{6,9 \times 10^{-7}} {\frac{cm^2}s}[/math]. Cząstkowa objętości właściwa białka wynosi [math]\bar{v} =\unit{0,749}{\frac{cm^3}{g}}[/math], a współczynnik lepkości wody w tej temperaturze jest równy [math]\eta = \unit{1,002}{ mPa\cdot s}[/math]. Oblicz promień uwodnionej cząsteczki białka i stopień uwodnienia. Stała gazowa [math]R = \unit{8,31}{ \frac J {Kmol}}[/math], liczba Avogadro [math]N_A = \unit{6,02\times 10^{23}} {\frac 1 {mol}}[/math].
Zadanie 4
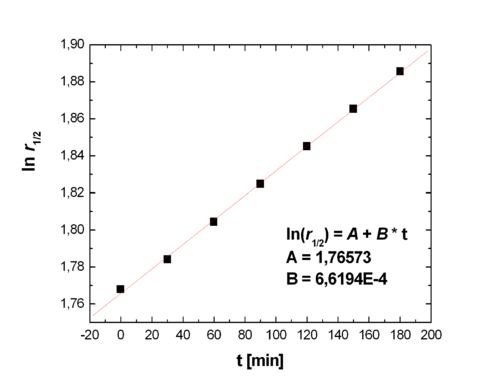
Współczynnik sedymentacji s wyznacza się często poprzez pomiar położenia środka granicy ([math]r_{\nicefrac{1}{2}}[/math]) w funkcji czasu. Roztwór białka o masie cząsteczkowej [math]M = \unit{74}{ kDa}[/math] i cząstkowej objętości właściwej [math]\bar{v} = \unit{0,737}{ \frac{cm^3}{g}}[/math] poddano wirowaniu w temperaturze [math]\unit{20}{^oC}[/math] z prędkością 52000 rpm (obroty na minutę). Gęstość buforu w tej temperaturze wynosi [math]\rho = \unit{1,01}{ \frac{g}{cm^3}}[/math], a współczynnik lepkości [math]\eta = \unit{1,002}{ mPa\cdot s}[/math]. Otrzymano następujące wyniki:
| t [min] | [math]r_{\nicefrac{1}{2}}[/math] [cm] | [math]\mathrm{ln}\left( r_{\nicefrac{1}{2}}\right)[/math] |
|---|---|---|
| 0 | 5,8591 | 1,76800 |
| 30 | 5,9541 | 1,78408 |
| 60 | 6,0763 | 1,80440 |
| 90 | 6,201 | 1,82471 |
| 120 | 6,3282 | 1,84502 |
| 150 | 6,4581 | 1,86534 |
| 180 | 6,5905 | 1,88563 |
Oblicz:
- współczynnik sedymentacji s,
- współczynnik tarcia f,
- współczynnik dyfuzji D,
- wartość [math]\nicefrac f{f_o}[/math], gdzie [math]f_o[/math] jest współczynnikiem tarcia dla cząsteczki sferycznej (nie uwodnionej).
Zadanie 5
Duże cząsteczki DNA kształtem przypominają wydłużoną elipsoidę obrotową. Współczynnik tarcia takiej cząsteczki wynosi w przybliżeniu [math]f = \frac{6π\eta a}{[ln(2a/b)]}[/math], gdzie [math]\eta[/math] — współczynnik lepkości rozpuszczalnika, a i b — odpowiednio długa i krótka oś elipsoidy. Cząsteczka DNA o masie cząsteczkowej [math]M = \unit{1000000}{ ma}[/math] długość około [math]\unit{5200}{\AA}[/math] i średnicę [math]\unit{22} {\AA}[/math]. Oblicz współczynnik dyfuzji D oraz współczynnik sedymentacji s dla tego DNA w [math]\unit{0,1}{ M}[/math] NaCl w temperaturze 20 °C. Gęstość buforu w tej temperaturze wynosi [math]\rho = \unit{1,0025}{\frac{ g}{cm^3}}[/math], jego współczynnik lepkości [math]\eta = \unit{1,016}{ mPa\cdot s}[/math], a cząstkowa objętość właściwa DNA [math]\bar{v}= \unit{0,556}{ \frac{cm^3}{g}}[/math].
Zadanie 6
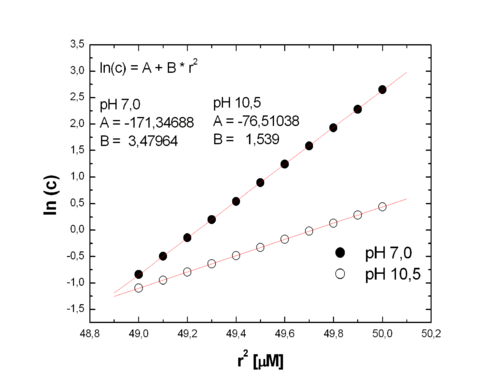
Dla pewnego białka przeprowadzono eksperyment wirowania równowagowego w temperaturze 20 °C w dwóch różnych pH: 7,0 i 10,5. Cząstkowa objętości właściwa białka wynosi [math]\bar{v} = \unit{0,749}{ \frac{cm^3}{g}}[/math], a gęstość buforu w tej temperaturze wynosi [math]\rho = \unit{0,9982}{\frac{ g}{cm^3}}[/math]. Prędkość wirowania wynosiła 30000 rpm w pH 7,0 i 40000 rpm w pH 10,5. Otrzymano następujące wyniki:
| [math]\unit{r^2}{ [cm^2]}[/math] | [math]\unit{c}{ [\mu M]}[/math], pH 7,0 | [math]\mathrm{ln}(c)[/math], pH 7,0 | [math]\unit{c}{ [\mu M]}[/math], pH 10,5 | [math]\mathrm{ln}(c)[/math], pH 10,5 |
|---|---|---|---|---|
| 49,0 | 0,431 | -0,84165 | 0,333 | -1,09961 |
| 49,1 | 0,611 | -0,49266 | 0,388 | -0,94675 |
| 49,2 | 0,865 | -0,14503 | 0,453 | -0,79186 |
| 49,3 | 1,22 | 0,19885 | 0,529 | -0,63677 |
| 49,4 | 1,72 | 0,54232 | 0,616 | -0,48451 |
| 49,5 | 2,44 | 0,892 | 0,72 | -0,3285 |
| 49,6 | 3,46 | 1,24127 | 0,84 | -0,17435 |
| 49,7 | 4,89 | 1,58719 | 0,98 | -0,0202 |
| 49,8 | 6,91 | 1,93297 | 1,14 | 0,13103 |
| 49,9 | 9,78 | 2,28034 | 1,33 | 0,28518 |
| 50,0 | 14,2 | 2,65324 | 1,55 | 0,43825 |
- Oblicz masę cząsteczkową białka w obydwu pH.
Wskazówka: w stanie równowagi sedymentacyjnej zachodzi:
- [math]ln(c) = \frac{M(1-\rho\bar{v})\omega^2r^2}{2RT} + \mathrm{const}[/math]
- Jak wytłumaczyć zależność masy cząsteczkowej od pH?