Rentgenografia
Spis treści
Zadanie 1
Dla dwuwymiarowej sieci pokazanej poniżej narysuj płaszczyzny sieciowe odpowiadające następującym wskaźnikom Millera: (010), (200), (110), (120), (320).
Zadanie 2
Dla kryształu należącego do układu regularnego uporządkuj w kierunku wzrastającej odległości międzypłaszczyznowej następujące zbiory płaszczyzn: (100), (320), (010), (120), (110).
Zadanie 3
Wyprowadź równanie Bragga.
Zadanie 4
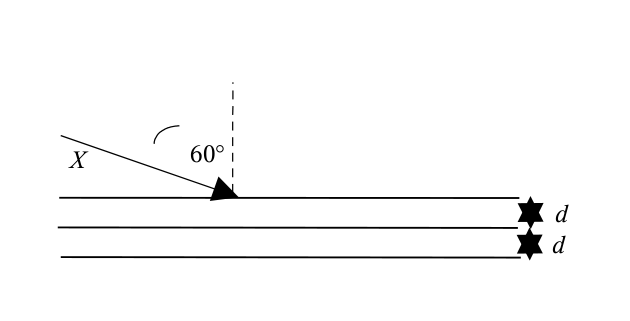
Wiązka promieniowania X o długości fali [math]\lambda = \unit{1,34}{ \AA}[/math] pada na kryształ NaCl pod kątem 60° w stosunku do pewnej rodziny płaszczyzn sieciowych odległych o [math]d = \unit{2,70}{ \AA}[/math] (patrz rysunek). O jakie kąty należy obracać kryształ wokół osi prostopadłej do płaszczyzny rysunku, aby w wyniku odbić od tych płaszczyzn powstawały maksima promieniowania ugiętego na krysztale?
Zadanie 5
Wiązka promieniowania X o długości fali [math]\lambda = \unit{1,537}{\AA}[/math] pada na kryształ aluminium. Odbicie pierwszego rzędu od płaszczyzny (111) zaobserwowano pod kątem [math]\theta = 19,2^o[/math]. Wyznacz masę atomową aluminium, wiedząc, że kryształ aluminium ma strukturę regularną centrowaną na ścianach, a gęstość aluminium wynosi [math]\rho = \unit{2699}{\frac{kg}{m^3}}[/math]. Liczba Avogadro jest równa [math]NA = \unit{6,02 \times 10^{23 }}{\frac 1{mol}}[/math].
Zadanie 6
Narysuj sieć odwrotną do dwuwymiarowej sieci rzeczywistej o parametrach [math]a = \unit 3 \AA,\ b = \unit 2 \AA,\ \gamma = 30^o[/math].
Zadanie 7
Jaka jest krótkofalowa granica widma ciągłego lampy rentgenowskiej przy napięciach pracy [math]U_1 =\unit{ 10}{ kV}[/math] i [math]U_2 =\unit{ 30}{ kV}[/math]?
- [math]e = \unit{1,602 \times 10^{-19}}C,\ h = \unit{6,626 \times 10^{-34}}{ Js},\ c = \unit{3 \times 10^8}{ \frac m s}[/math]
Zadanie 8
Oblicz długość fali charakterystycznego promieniowania rentgenowskiego linii [math]\mathrm{K}_\alpha[/math] i [math]\mathrm{K}_\beta[/math] dla miedzi (Z = 29) i molibdenu (Z = 42). Skorzystaj z zależności Moseleya:
- [math]\lambda = \frac{1}{R(Z-\sigma)^2\cdot \left( \frac 1{n^2_k}-\frac 1{n^2_p}\right)}[/math]
gdzie: R — stała Rydberga, Z — liczba atomowa pierwiastka, σ — stała ekranowania, dla serii K [math]\sigma = 1, nk[/math] — główna liczba kwantowa powłoki, na którą następuje przeskok elektronu, [math]n_p[/math] — główna liczba kwantowa powłoki, z której następuje przeskok elektronu. [math]R = \unit{1,097 \times 10^7}{\frac 1 m}[/math], ZCu = 29, ZMo = 42