TI/Numpy

Pakiet Numpy

Moduł Numpy jest podstawowym zestawem narzędzi dla języka Python umożliwiającym zaawansowane obliczenia matematyczne, w szczególności do zastosowań naukowych (tzw. obliczenia numeryczne, jak mnożenie i dodawanie macierzy, diagonalizacja czy odwrócenie, całkowanie, rozwiązywanie równań, itd.). Daje on nam do dyspozycji specjalizowane typy danych, operacje i funkcje, których nie ma w typowej instalacji Pythona. Natomiast moduł Scipy pozwala na dostęp do bardziej złożonych i różnorodnych algorytmów wykorzystujących bazę zdefiniowaną w Numpy.

Przedstawimy tutaj tylko wstęp do Numpy. Wynika to z faktu, że opisanie licznych funkcji dostępnych w bibliotece Numpy jest ogromną pracą, która zupełnie nie ma sensu — równie dobrze można zajrzeć bezpośrednio do źródła, http://docs.scipy.org/doc/numpy/reference/.

Najważniejszym obiektem, na którym bazuje pakiet Numpy i szereg pakietów z niego korzystających jest klasa ndarray wprowadzająca obiekty array. Obiekty array możemy traktować jako uniwersalne pojemniki na dane w postaci macierzy (czyli wektorów lub tablic). W porównaniu ze standardowymi typami sekwencji Pythonowych (lista, krotka) jest kilka różnic w operowaniu tymi obiektami:

1. obiekty przechowywane w macierzy array muszą być wszystkie tego samego typu;
2. obiekty array zachowują swój rozmiar; przy zmianie rozmiaru takiego obiektu powstaje nowy obiekt, a obiekt sprzed zmiany zostaje usunięty;
3. obiekty array wyposażone są w bogaty zestaw funkcji operujących na wszystkich przechowywanych w obiekcie danych, specjalnie optymalizowanych do przetwarzania dużych ilości danych. Jak to działa zostanie zaprezentowane poniżej.

Tworzenie

Najprostszym sposobem stworzenia macierzy Numpy jest wywołanie funkcji array z argumentem w postaci listy liczb. Jeśli zamiast listy liczb użyjemy listy zawierającej inne listy (tzw. listy zagnieżdżone), to otrzymamy macierz wielowymiarową. Na przykład jeśli listy są podwójnie zagnieżdzone, to otrzymujemy macierz dwuwymiarową (tablicę).

# przykład wykorzystania Numpy
>>> import numpy
>>> A = numpy.array([1, 3, 7, 2, 8])
array([1, 3, 7, 2, 8])
>>> B = numpy.array([[1, 2, 3], [4, 5, 6]])
>>> B
array([[1, 2, 3],
       [4, 5, 6]])
>>> B.transpose()
array([[1, 4],
       [2, 5],
       [3, 6]])

Innym sposobem tworzenia macierzy jest funkcja numpy.arange, która działa analogicznie do range, tyle tylko, że zwraca macierz zamiast listy. Argumenty są takie same:

1. indeks początkowy [opcjonalnie, domyślnie 0]
2. indeks następny po końcowym
3. krok [opcjonalnie, domyślnie 1]

>>> numpy.arange(1000000)
array([     0,      1,      2, ..., 999997, 999998, 999999])

Jak było już wspomniane, w przypadku macierzy array typowe operacje matematyczne możemy przeprowadzić dla wszystkich elementów macierzy przy użyciu jednego operatora lub funkcji. Zachowanie takie jest odmienne niż w przypadku list czy innych sekwencji Pythona. Jeśli chcielibyśmy na przykład pomnożyć wszystkie elementy listy L przez liczbę a, musimy użyć pętli:

L = [1, 3, 5, 2, 3, 1]
for i in L:
    L[i]=L[i]*a

Natomiast mnożenie wszystkich elementów macierzy M przez liczbę a wygląda tak:

M = numpy.array([1, 3, 5, 2, 3, 1])
M = M*a

Operacje wykonywane od razu na całych macierzach mają wiele zalet. Kod programu jest prostszy i krótszy, przez co mniej podatny na błędy. Poza tym nie musimy przejmować się konkretną realizacją danej operacji — robi to za nas funkcja pakietu Numpy, która jest specjalnie optymalizowana, żeby działała jak najszybciej.

Inne

zob.numpy.mgrid, numpy.ogrid, numpy.linspace, numpy.zeros, numpy.ones, numpy.r_.

Wydobywanie danych

Pojedyncze liczby

Dostęp do elementów (i pod-macierzy) jest możliwy poprzez wykorzystanie notacji indeksowej (macierz[i]) jak i wycinkowej (macierz[i:j]).

Dostęp do pojedynczego elementu:

>>> A = array([[1, 2, 3],[4,5,6]])
>>> A
array([[1, 2, 3],
       [4, 5, 6]])
>>> A[0][2]    # podobnie jak w Pythonie,numeracja od 0
3
>>> A[0, 2]
3

Indeksy dotyczące poszczególnych wymiarów można oddzielić przecinkami.

Macierz A jest tablicą dwuwymiarową, i sposób numerowania zawartych w niej obiektów jest następujący: pierwszy indeks przebiega pierwszy wymiar (wybiera wiersz), drugi indeks przebiega drugi wymiar (wybiera kolumnę).

Pod-macierze

Dostęp do pod-macierzy:

>>> A[1]             # wiersz 1
array([4, 5, 6])
>>> A[1, :]          # wiersz 1, wszystkie kolumny
array([4, 5, 6])
>>> A[:, 1]          # wszystkie wiersze, kolumna 1
array([2, 5])

Jak widać, ograniczenie się do pojedynczego punktu w danym wymiarze, powoduje degenerację tego wymiaru. Uzyskuje się macierz, w której liczba wymiarów jest mniejsza o jeden.

>>> A[:, 1:]
array([[2, 3],
       [5, 6]])

W pierwszym wymiarze (wiersze) bierzemy wszystko, natomiast w drugim od 1 do końca. Efektywnie wycinamy kolumnę 0.

Indeksowanie macierzy macierzami

Do wybrania elementów z macierzy można tez użyć innej macierzy. Może to być

• macierz liczb — wówczas są one traktowane jako indeksy. Wybieramy te elementy, które uzyskalibyśmy indeksując każdym z indeksów z osobna
• macierz wartości logicznych (boolean) rozmiaru macierzy z danymi. Wybieramy te elementy, którym odpowiada True w macierzy indeksującej.

Uwaga: W wyniku dostajemy macierz jedno wierszową.

Przykład

>>> print A
[[1 2 3]
 [4 5 6]]
>>> print A > 2
[[False False  True]
 [ True  True  True]]
>>> print A[A > 2]
[3 4 5 6]
>>> print A[A % 2 == 0]
[2 4 6]

Więcej: http://docs.scipy.org/doc/numpy/user/basics.indexing.html

Porównanie liczb w Numpy i liczb w Pythonie

Przejście od Pythona do Numpy oznacza odejście od obiektowości. Oczywiście takie stwierdzenie można natychmiast skontrować:

    numpy.random.random((10,10)).var()

jest typowym przykładem notacji obiektowej, i generalnie ma cechy obiektowości (ukrywanie detali implementacji, polimorfizm). Odejście od obiektowości występuje tylko na poziomie indywidualnych elementów — liczb.

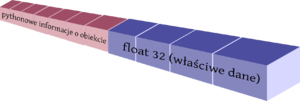
W Pythonie, tak jak w zasadniczej większości języków programowania, operacje na liczbach są ostatecznie wykonywane przez procesor, w identyczny sposób niezależnie od języka programowania. A procesor, jak wiadomo, umie wykonywać tylko proste operacje. Przez to liczby, które się mu podaje by wykonać na nich działania, są w ściśle określonym formacie, niezależnym od języka programowania. Tak więc obiekt w Pythonie, np. liczba zmiennoprzecinkowa, zawiera pewne meta-informacje o tym obiekcie (jak reference-count, czyli liczba użytkowników obiektu, i typ, czyli przypisanie do klasy) oraz właściwe dane, w formacie oczekiwanym przez procesor.

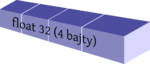
Rysunki powyżej przedstawiają schematycznie zmienną w Pythonie (typu float) i pojedynczy element macierzy numpy.ndarray. W przypadku architektury 32-bitowej, liczba float ma 4 bajty (32 bity), a cały obiekt 12 bajtów, czyli 96 bitów).

Odejście od obiektowości w Numpy oznacza zatracenie obiektowości indywidualnych elementów macierzy, natomiast sam obiekt numpy.ndarray bardzo silnie wykorzystuje notację i właściwości podejścia obiektowego. Indywidualne elementy macierzy muszą być tego samego typu — oznacza to ten sam rozmiar w bajtach oraz identyczną interpretację i zachowanie każdego elementu.

Można powiedzieć, że numpy.ndarray rezygnuje z części możliwości na rzecz wydajności, przed wszystkim różnorodności typów przedstawionej jak na rysunku poniżej.

„Eksport” danych z Numpy do Pythona

Każda liczba w Pythonie jest indywidualnym obiektem. Liczby w Numpy takie nie są. Niemniej, kiedy wybierzemy jeden element z macierzy (np. używając []), to otrzymujemy liczbę-obiekt. Numpy automatycznie tworzy nowe obiekty do przechowywania liczb które mają być użyte poza Numpy.

Specjalne wartości liczbowe

Pakiet Numpy wprowadza też szczególne wartości dla przechowywania nietypowych wyników obliczeń. Należą tutaj takie wartości jak:

• inf opisująca wartość nieskończoną. Są dostępne również jej następujące warianty: PINF odpowiada wartości +∞, natomiast NINF wartości −∞. Do sprawdzenia czy badana zmienna x zawiera „normalną” czy nieskończoną wartość używamy funkcji isfinite(x) pakietu Numpy. Zwraca ona False w przypadku napotkania wartości nieskończonej w zmiennej x.
• NaN opisującą nie-liczbę (przechowywaną w zmiennej liczbowej, NaN to skrót od angielskiego not a number), wartość, która nie reprezentuje żadnej liczby. Wartość taka pojawia się w przypadku próby wykonania pewnych niedozwolonych operacji matematycznych lub sygnalizuje wystąpienie wyniku takiej operacji. Warto tutaj zauważyć, że porównanie numpy.NaN == numpy.NaN daje wynik False. Aby sprawdzić czy mamy do czynienia z taką wartością używamy funkcji isnan pakietu Numpy.

Jakkolwiek wartości te nie są dostępne w standardowym Pythonie, są one zestandaryzowane i opisane w normie IEEE-754; zapisane w pliku binarnym będą poprawnie interpretowane przez inne programy stosujące się do tej normy.

Dlaczego warto używać Numpy?

Pierwsza przyczyna, zazwyczaj najmniej istotna, to wydajność. Jeśli mamy pomnożyć 100 elementów, to szybkość operacji na pojedynczym elemencie nie ma znaczenia. Podobnie jest z rozmiarem pojedynczego elementu. Jeśli elementów jest 10⁶, to również wtedy narzut nie ma większego znaczenia. Policzmy: 1000000 razy 12 bajtów, to 12 MB. Typowy komputer ma obecnie 1-4 GB pamięci, czyli używamy od 1,2% do 0,27% dostępnej pamięci — jaki problem? Dopiero gdy miejsce zajmowane przez dane jest tego samego rzędu co całość dostępnej pamięci, to czy pojedyncza komórka zajmuje 8 czy 16 bajtów, zaczyna mieć znaczenie.

Druga przyczyna, istotna ze względu na przyjemność pracy, to notacja obiektowa i infixowa. Ta pierwsza to oczywiście „notacja z kropką” — dostęp do metod i atrybutów na obiekcie. Jej użycie, zwłaszcza w połączeniu z dopełnieniem TAB-em upraszcza pisanie. Przykład notacji obiektowej:

a.transpose().min()
# zamiast
numpy.min(numpy.transpose(a))

Ta druga (infixowa) to stara dobra „notacja matematyczna” — umiejscowienie operatorów dwuargumentowych pomiędzy obiektami na które działają. Przykład notacji infixowej:

a + b*c
# zamiast
numpy.add(a, numpy.multiply(b, c))

Oczywiście notacja obiektowa i infixowa jest używane wszędzie w Pythonie, ale warto wspomnieć, że Numpy od niej nie odchodzi. Niemniej Numpy odchodzi od Pythonowej interpretacji niektórych działań. W Pythonie takie operacje jak mnożenie list wywodzą się z działań na ciągach znaków. W obliczeniach numerycznych podstawą są działania na elementach, tak więc w Numpy wszystkie operatory domyślnie działają na indywidualnych parach elementów.

Trzecia przyczyna, chyba najważniejsza, to biblioteka funkcji numerycznych. Odejście od obiektowości danych pozwala na eksport wartości i komunikację z bibliotekami napisanymi w zupełnie innych językach programowania. Na przykład Scipy może korzystać z biblioteki LAPACK (Linear Algebra PACKage, napisanej w Fortranie 77). To że funkcje napisane w różnych językach mogą wymieniać się danymi w pamięci bez skomplikowanego tłumaczenia danych, wynika z faktu, że tak jak to w poprzednim podrozdziale było opisane, ostatecznie wszystkie liczby są w formacie akceptowanym przez procesor.

Możliwość użycia kodu napisanego w C czy Fortranie pozwala na wykorzystanie starych, zoptymalizowanych, sprawdzonych rozwiązań.

Podsumowanie

Normalnie programista Pythona takie detale, jak ile bitów ma zajmować zmienna, pozostawia całkowicie w gestii interpretera. Niemniej w przypadku obliczeń numerycznych często potrzebna jest silniejsza kontrola. Numpy daje możliwość dokładnej kontroli formatu danych, czyli odejście od pomocniczości powszechnej w Pythonie, pozwalając jednocześnie na gładkie łączenie obliczeń na macierzach z Numpy i normalnych obiektach pythonowych.

Zadanka

Zob. zadania z operacji na macierzach.