
TI/Wstep
Spis treści
⬆ Python
Stworzony dla Was kurs Pythona jest dostępny pod adresem Programowanie z Pythonem 3. Na wykładzie omówimy tylko ogólne kwestie, i powtarzać będziemy najważniejszą dla Was informację:
Programowania nie da się nauczyć — nawet z najlepszych materiałów — na dzień przed egzaminem czy kolokwium. Programowanie to nie tylko wiedza o składni i regułach języka, ale przede wszystkim umiejętność ich stosowania w praktyce, którą można posiąść tylko pisząc programy.
Dlatego właśnie zachęcamy Was do zainstalowania Pythona na Waszych komputerach — abyście mieli możliwość ćwiczenia nie tylko w czasie zajęć.
W odróżnieniu od niektórych pakietów stosowanych w obliczniach naukowych, jak np. Matlab(R) czy Mathematica(R), intepretery języka Python dostępne są na otwartych licencjach — czyli również za darmo — dla wszystkich ważniejszych systemów operacyjnych. O tym jak to możliwe, że najwyższej jakości Wolne Oprogramowanie (ang. Free Software) dostępne jest dla wszystkich za darmo i z kodem źródłowym, i dlaczego podkreślamy wolne jak w słowie 'wolność' ("free as in "freedom", not "free as in free beer") dowiecie się z rozdziału Otwarte Źródła, GNU i wolność oprogramowania. Na razie wystarczy wiedza, że Pythona dla Windows, macOS czy GNU/Linuksa możemy ściągnąć z Internetu legalnie i za darmo. Warto tylko pamiętać, że używać będziemy wersji 3.xx Pythona. Nieważne, co stoi po "3" — może być 3.2, 3.4 czyli 3.x. Ważne, że w poprzednich wersjach różniących się głównym numerem, czyli 2.xx (ostatnią stabilną wersją była 2.7) różni się trochę składnia języka, więc nie wszystkie polecenia których uczycie się na ćwiczeniach będą działać tak samo.
Te informacje powinny Wam wystarczyć do zainstalowania Pythona na swoim komputerze domowym, w Waszym ulubionym systemie operacyjnym. Na ćwiczeniach będziemy używać Pythona w systemie GNU/Linux. Linux to również Wolne Oprogramowanie, które możecie ściągnąć i legalnie za darmo zainstalować na swoim komputerze.
Terminal
...to okienko, w którym wpisujemy komendy intepretowane przez system operacyjny, a konkretnie powłokę systemową (shell). Te okienka to formalnie emulatory terminali, bo historycznie terminal to było urządzenie (najczęściej monitor i klawiatura), za pomocą którego można się było komunikować z komputerem wyłącznie w trybie tekstowym. Pomimo tego, że współczesne komputery oferują w pełni graficzny interfejs, wiersz poleceń to wciąż w wielu przypadkach najefektywniejszy i najnaturalniejszy sposób komunikacji z systemem operacyjnym i uruchamiania programów.
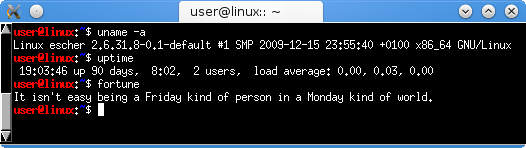
uname (podaje wersję systemu), uptime (podaje czas jaki upłynął od startu komputera) i fortune (emuluje ciasteczko w chińskiej knajpie). Po wykonaniu każdej komendy wyświetlany jest (w tym przypadku) czerwono-niebieski znak gotowości (ang. prompt).W przypadku systemów Uniksowych — do których należy GNU/Linux — podstawowe polecenia pozostają niezmienione od zarania dziejów (tzn. od zarania dziejów Uniksa), czyli od roku 1969. I wszystko wskazuje na to, że pozostaną z nami jeszcze przez wiele lat, więc wiedza na ich temat nie zdeaktualizuje się za szybko. Jest to ciekawe samo w sobie w świecie, w którym interfejs programów (nie tylko systemów operacyjnych) zmienia się czasami znacząco nawet z wersji na wersję.
Co to za zaklęcia?
Listę ważniejszych poleceń Uniksa znajdziesz np. w Wikipedii. Ogólnie:
- Na początku zawsze musimy wpisać nazwę programu albo polecenia systemowego. Po wciśnięciu
Enterprogram — jeśli takowy jest w systemie zainstalowany, a dostęp do katalogu w którym się znajduje jest uwzględniony w tzw. ścieżce (PATH) — powinien się uruchomić. - Po spacji — przed wciśnięciem
Enter— możemy też wpisać:- argment(y), czyli np. nazwę pliku którą ma od razu otworzyć wywołany program, oraz
- opcje, czyli przełączniki dla programu (np. wpisanie
ls -lwywołuje polecenie systemowels, wypisujące zawartość bieżącego katalogu, z opcją-l, dającą dokładniejszy (czyli długi, anglong) listing.
- W większości powłok Uniksowych możemy w trakcie wpisywania polecenia wcisnąć klawisz tabulatora
Tab, wtedy system inteligentnie dopełni wpisany tekst do pełnej nazwy zainstalowanego programu lub polecenia systemowego, lub, jeśli dopełnienie nie jest jednoznaczne, wyświetli listę opcji.
Prawa dostępu do plików
durka@MacBook-Air pokaz% pwd /Users/durka/pokaz durka@MacBook-Air pokaz% ls silnia.py witajcie witka.py durka@MacBook-Air pokaz% ls -l total 24 -rw-------@ 1 durka staff 62 2 paź 20:32 silnia.py -rwxr-xr-x@ 1 durka staff 51 3 paź 09:11 witajcie -rw-r--r--@ 1 durka staff 60 2 paź 20:35 witka.py durka@MacBook-Air pokaz % ls -lh total 24 -rw-------@ 1 durka staff 62B 2 paź 20:32 silnia.py -rwxr-xr-x@ 1 durka staff 51B 3 paź 09:11 witajcie -rw-r--r--@ 1 durka staff 60B 2 paź 20:35 witka.py durka@MacBook-Air pokaz % ls -la total 32 drwxr-xr-x 6 durka staff 192 3 paź 09:16 . drwxr-xr-x+ 56 durka staff 1792 3 paź 09:09 .. -rw-r--r-- 1 durka staff 4 3 paź 09:16 .ukryty_plik -rw-------@ 1 durka staff 62 2 paź 20:32 silnia.py -rwxr-xr-x@ 1 durka staff 51 3 paź 09:11 witajcie -rw-r--r--@ 1 durka staff 60 2 paź 20:35 witka.py durka@MacBook-Air pokaz %
Nie tylko GNU/Linux
- W MS Windows konsolę można uruchomić poleceniem "Wykonaj program", wpisując jako program
cmd— zapewne skrót od command line. Polecenia powłoki Windows różnią się od poleceń Uniksa, wywodzą się z systemu MS DOS. - MacOS od wersji X jest, wbrew pozorom, pełnokrwistym systemem Uniksowym, i "Terminal" jest jego częścią.
Interfejs graficzny
Współczesne systemy oferują oczywiście interfejs graficzny. Z pozoru różny w różnych systemach, z dość oczywistych przyczyn opiera się we wszystkich systemach na tych samych ogólnych regułach. W czasach codziennego intensywnego obcowania z różnymi programami Reguły te "czujemy intuicyjnie", więc można ich opis zastąpić hasłem "Koń jaki jest, każdy widzi", ale dla zainteresowanych polecamy opis z książki wydanej w roku 2000 (jak widać podstawowe reguły również tutaj są w miarę niezmienne), w osobnym rozdziale o interfejsie graficznym.
Jak to się ma do klikania?
- Jeśli klikamy ikonę symbolizującą program, system po prostu ten program uruchomi. Nie mamy możliwości od razu podać np. w jakim trybie program chcemy uruchomić, czy jaki plik powinien być od razu wczytany.
- Jeśli klikamy ikonę pliku, system stara się odnaleźć program "właściwy" dla otwarcia danego pliku. Normalne kliknięcie otwiera plik w programie, który znajduje się na pierwszym miejscu systemowej listy programów "potrafiących" wyświetlić dany plik. Kliknięcie prawym guzikiem otwiera zwykle menu kontekstowe, z którego możemy wybrać do otwarcia pliku jeden z programów zarejestrowanych w systemie.
Wartości logiczne
Jak wiadomo, logika rządzi się swoimi prawami. Pozwalają one na ścisłe wyliczanie wartości logicznej zdań — czyli po prostu określenie, czy zdanie złożone z prostszych zdań jest prawdziwe czy też fałszywe. Ponieważ występują tylko dwie wartości i można dla nich pisać równania, to zasady logiki nazywamy algebrą dwuwartościową, lub częściej [algebrą Boole'a], od nazwiska osoby która pierwsza sformalizowała ten rachunek.
Dwie wartości, prawdę i fałsz, oznaczamy często jako 1 i 0. W Pythonie jako wartość oznaczającą prawdę można użyć liczby 1 albo specjalnego obiektu True, natomiast fałsz — liczby 0 lub obiektu False. Te specjalne obiekty nazywane są po angielsku booleans, co należy rozumieć jako wartości Boole'a. Nie są niezbędne i zostały wprowadzone po to, by podkreślić kiedy używamy algebry dwuwartościowej, a kiedy zwykłej.
Operacje logiczne
| Suma | Iloczyn | Negacja |
|---|---|---|
| [math]\cup[/math] | [math]\cap[/math] | [math]\sim[/math] |
| [math]+[/math] | [math]\cdot[/math] | [math]\overline{a}[/math] |
| [math]+[/math] | [math]\cdot[/math] | [math]-[/math] |
| [math]\lor[/math] | [math]\land[/math] | [math]\lnot[/math] |
| [math]|[/math] | [math]\&[/math] | [math]![/math] |
| [math]OR[/math] | [math]AND[/math] | [math]NOT[/math] |
Koniunkcja
Jeśli mamy dwa zdania a oraz b, ich koniunkcją nazywamy wyrażenie, które jest prawdziwe gdy obywa zdania są prawdziwe. W matematyce oznacza się to przez [math]a \wedge b[/math]. W Pythonie operatorem koniunkcji jest and.
Możemy wypisać działanie operatora na każdą możliwą parę wartości logicznych:
wartości zdań wartość ich koniunkcji a b a and b True True True True False False False True False False False False
Koniunkcję nazywa się często iloczynem logicznym, bo jeśli oznaczymy prawdę i fałsz przez 1 i 0, to zwykłe mnożenie tych dwóch liczb daje taki sam wynik jak koniunkcja.
Alternatywa
Jeśli mamy dwa zdania a oraz b, ich alternatywą nazywamy wyrażenie, które jest prawdziwe gdy przynajmniej jedno z tych zdań jest prawdziwe. W matematyce oznacza się to przez [math]a \vee b[/math]. W Pythonie operatorem alternatywy jest or.
Ponownie, najłatwiej przedstawić działanie operatora w tabelce ze wszystkimi możliwymi parami wartości logicznych:
wartości zdań wartość ich alternatywy a b a or b True True True True False True False True True False False False
Alternatywę nazywa się często sumą logiczną, bo jeśli ponownie oznaczymy prawdę i fałsz przez 1 i 0, to zwykłe dodawanie tych dwóch liczb daje taki sam wynik jak koniunkcja, za wyjątkiem 1 + 1. W wypadku sumy logicznej dwóch zdań prawdziwych wynik i tak jest 1, bo w algebrze Boole'a po prostu nie ma większej liczby.
Zaprzeczenie
Jeśli mamy zdanie a, jego zaprzeczeniem nazywamy wyrażenie, które jest prawdziwe tylko gdy to zdanie jest fałszywe.
Tutaj tabelka możliwości jest krótsza, bo mamy tylko jedno zdanie:
wartość zdania wartość jego zaprzeczenia a not a True False False True
Wartość logiczna wyrażeń w Pythonie
Kiedy używamy operatorów przyrównania (==, !=, <=, >=, <, >), w wyniku otrzymujemy jedną z dwóch wartości logicznych True / False. Większość innych wyrażeń nie jest prawdziwa lub fałszywa w sensie matematycznym. Na przykład napis "Hello, World" nie ma wartości logicznej w sensie matematycznym. Niemniej w Pythonie, jak też w wielu innych językach programowania, wszystkie obiekty mają wartość logiczną określaną zgodnie z pewnymi ustalonymi regułami. Pozwala to wykorzystać dowolne wyrażenie jako warunek w poleceniu sterujących wykonaniem programu, jak if czy while, bo każde wyrażenie zwraca jakiś obiekt.
W przypadku obiektów które nie są po prostu True ani False, to czy dany obiekt zostanie zinterpretowany jako prawdziwy, czy też jako fałszywy, rządzi się paroma prostymi regułami:
- w przypadku liczb, liczba 0 jest fałszywa, wszystkie pozostałe są prawdziwe
- w przypadku sekwencji (np. napisów) i innych kolekcji, tylko te puste, o długości 0, są fałszywe
- pozostałe obiekty są prawdziwe (o ile ich twórca nie podjął specjalnych działań by mogły mieć różne wartości logiczne)
Obliczanie wartości wyrażeń logicznych w Pythonie
Jeśli napiszemy wyrażenie zawierające operatory and lub or, często możemy określić wartość logiczną całego wyrażenia bez znajomości wartości logicznej drugiego operandu. Pozwala to na pominięcie części obliczeń, tzw. wykonanie warunkowe (ang. short-circuiting). Mówiąc bardziej konkretnie,
- w przypadku operatora and, jeśli pierwszy wyraz jest fałszywy, to drugi nie jest obliczany bo wiadomo, że całe wyrażenie jest fałszywe,
- w przypadku operatora or, jeśli pierwszy wyraz jest prawdziwy, to drugi nie jest obliczany, bo wiadomo, że całe wyrażenie jest prawdziwe.
W przedstawionych powyżej tabelkach przedstawiającej działanie operatorów and lub or na wartości logiczne True i False argumentami były wszystkie możliwe kombinacje tych dwóch wartości. Później zostały przedstawione reguły pozwalająca na nadanie wartości logicznej każdemu wyrażeniu. W przypadku gdy jako argumentu w koniunkcji lub alternatywie użyje się obiektu, który nie jest wartością logiczną True albo False, to wynik wyrażenia logicznego też może nie być wartością logiczną.
Tabelki działania operatorów pozostają w mocy, ale aby uwzględnić działanie na nie-booleans i wykonanie warunkowe, do wykonywania operatorów logicznych używa się następujących reguł:
- x and y — jeżeli x jest fałszem, zwraca x, w przeciwnym wypadku zwraca y
- x or y — jeżeli x jest prawdą, zwraca x, w przeciwnym wypadku zwraca y
Wyniki działania tych reguł dla wartości True i False dają to co powinny. Natomiast w innych przypadkach pozwalają na budowanie pseudo-zdań logicznych. Np. jeśli prosimy użytkownika o wpisanie pewnego napisu, ale w przypadku gdy wpisał napis pusty chcemy użyć wartości domyślnej, możemy wykorzystać alternatywę:
print (napis or "(podałeś pusty napis)")
# napis o długości 0 jest fałszywy,
# w takim wypadku zostanie użyty drugi operand
Przedstawione powyżej reguły obliczania koniunkcji i alternatywy są równoważne następującemu przepisowi:
- Zaczynamy od obliczenia wartości lewego operandu.
- Jeśli wartość logiczna lewego operandu nie pozwala na rozstrzygnięcie wartości logicznej całego wyrażenia, obliczamy wartość prawego operandu.
- Jako wynik zwracamy ostatni obliczony operand, czyli ten który rozstrzyga o wartości logicznej całego wyrażenia.
