TI/Wybrane zagadnienia numeryczne
Spis treści
Rozwiązywanie równań liniowych
- Przykład:
Rozwiązanie układu równań liniowych:
- [math]
\left\{ \begin{array}{l}
x_1+3x_3=3\\
2x_1+x_2+5x_3=2\\
4x_1+8x_2+8x_3=1
\end{array} \right.
[/math]
- [math]
\left\{ \begin{array}{l}
x_1+3x_3=3\\
2x_1+x_2+5x_3=2\\
4x_1+8x_2+8x_3=1
\end{array} \right.
[/math]
import numpy as np
A = np.array([[1, 0, 3],
[2, 1, 5],
[4, 8, 8]])
b = np.array([3, 2, 1])
x = np.linalg.solve(A, b)
print x
- Rezultat
[-12.75 1.25 5.25]- Jak to działa?
Nasz wyjściowy układ równań liniowych możemy zapisać w postaci macierzowej [math]Ax=b[/math]:
- [math]
\begin{array}{cccc}
\left( \begin{array}{ccc}1 & 0 & 3\\2 & 1 & 5\\4 & 8 & 8\end{array} \right)&
\left( \begin{array}{c}x_1\\x_2\\x_3\end{array} \right)&
=&
\left( \begin{array}{c}3\\2\\1\end{array} \right)\\
\ &\ &\ &\ \\
A&x&\ &b \end{array}
[/math].
- [math]
\begin{array}{cccc}
\left( \begin{array}{ccc}1 & 0 & 3\\2 & 1 & 5\\4 & 8 & 8\end{array} \right)&
\left( \begin{array}{c}x_1\\x_2\\x_3\end{array} \right)&
=&
\left( \begin{array}{c}3\\2\\1\end{array} \right)\\
\ &\ &\ &\ \\
A&x&\ &b \end{array}
[/math].
Macierz [math]A[/math] konstruujemy ze współczynników mnożących zmienne [math]x_1[/math], [math]x_2[/math] i [math]x_3[/math] w poszczególnych równaniach — każdy wiersz macierzy [math]A[/math] opisuje jedno równanie, każda jej kolumna opisuje kolejno jedną z niewiadomych zmiennych [math]x_i[/math]. Po pomnożeniu [math]A[/math] przez wektor [math]x[/math], którego każdy wiersz zawiera odpowiednią niewiadomą, otrzymamy lewą stronę naszego układu równań. Prawą stronę tworzy wektor [math]b[/math], którego wiersze utworzone są odpowiednio z prawych stron poszczególnych równań układu.
Funkcja solve modułu Numpy zwraca nam listę zawierającą poszukiwane przez nas rozwiązanie układu równań: x1 = −12,75, x2 = 1,25, x3 = 5,25.
- Inne podejście
Możemy zauważyć, że rozwiązanie układu równań można formalnie uzyskać mnożąc obie strony równania (lewostronnie) przez macierz odwrotną do A:
- [math] \begin{array}{l} Ax=b\quad\quad\quad\quad\quad\quad \mid A^{-1}\cdot \\ \underbrace{A^{-1}\cdot A}_{=1} \cdot x=A^{-1} \cdot b \\ x=A^{-1}b \end{array} [/math]
W poniższym przykładzie do odwrócenia macierzy A stosujemy funkcję inv z modułu numpy.linalg. Mnożenie macierzy realizuje zaś funkcja dot.
# -*- coding: utf-8 -*-
import numpy as np
A = np.array([[1, 0, 3],
[2, 1, 5],
[4, 8, 8]])
b = np.array([3, 2, 1])
A1 = np.linalg.inv(A)
print "Macierz odwrotna do A:"
print A1
print "Sprawdzenie macierzy odwrotnej:"
print np.dot(A1, A)
x = np.dot(A1, b)
print "Rozwiązanie:"
print x
- Rezultat
Macierz odwrotna do A:
[[-8. 6. -0.75]
[ 1. -1. 0.25]
[ 3. -2. 0.25]]
Sprawdzenie macierzy odwrotnej:
[[ 1.00000000e+00 1.77635684e-15 1.77635684e-15]
[ -1.11022302e-16 1.00000000e+00 -2.22044605e-16]
[ -2.22044605e-16 -4.44089210e-16 1.00000000e+00]]
Rozwiązanie:
[-12.75 1.25 5.25]
Wyrażenia lambda
W takich obliczeniach jak te opisywane w niniejszym rozdziale, występuje potrzeba definiowania króciusieńkich funkcji. Okazuje się, że można je definiować na dwa sposoby:
- zwyczajnie, z wykorzystaniem słowa kluczowego def,
- jako tzw. wyrażenie λ, z wykorzystaniem słowa kluczowego lambda.
Po słowie kluczowym lambda podajemy nazwy, które będą pełnić rolę zmiennych w naszej funkcji, a po dwukropku wypisujemy wyrażenie (używając podanych przed dwukropkiem nazw jako zmiennych).
>>> def f(x): return x**3
...
>>> print f
<function f at 0x1c285f0>
>>> f1 = f
>>> print f1
<function f at 0x1c285f0>
>>> g = lambda x: x**3
>>> print g
<function <lambda> at 0x1c286e0>W tym przykładzie, funkcje f, f1 i g działają tak samo — biorą jeden argument i zwracają jego sześcian. Różnica jest taka, że funkcja f „wie” że nazywa się „f”, co widać w napisie wypisywanym po print f czy print f1. Natomiast funkcja g nazywa się „<lambda>”, tak samo jak wszystkie inne funkcje zdefiniowane jako wyrażenie λ, czyli nie ma swojej nazwy. Zmienna g jest tylko dowiązaniem do obiektu funkcji, tak samo jak zmienna f1.
Funkcja zdefiniowana jako wyrażenie λ jest równoważna funkcji definiowanej zwyczajnie zwracającej to samo wyrażnie. Niemniej, większości rzeczy które można zrobić w funkcji, nie można zrobić w wyrażeniu λ ze względu na ograniczenia składni:
- Wyrażenie λ musi być pojedynczym wyrażeniem.
- Wyrażenie λ nie może zawierać docstringa.
Wyrażenia λ są wygodne ze względu na to, że wymagają mniej stukania w klawisze.
Rozwiązywanie równań dowolnych
import scipy.optimize as so
def func(x):
return x**3 + 3. * x - 0.3
print so.fsolve(func, 0.5)
print so.fsolve(lambda x: x**3 + 3*x - 0.3, 0.5)
- Rezultat:
0.099669956223525716
0.099669956223525716- Jak to działa?
Funkcja fsolve z modułu scipy.optimize poszukuje miejsc zerowych funkcji, czyli takich wartości x, dla których [math]f(x)=0[/math]. Załóżmy, że chcemy rozwiązać równanie:
[math]x^3+3x=0,3[/math].
Po przepisaniu tego równania do postaci
[math]x^3+3x-0,3=0[/math]
widzimy, że rozwiązanie tego równania jest równoważne poszukiwaniu miejsc zerowych funkcji:
[math]f(x)=x^3+3x-0,3[/math].
Funkcja fsolve oczekuje badanej funkcji jako pierwszego argumentu. Możemy tu przekazać nazwę funkcji osobno zdefiniowanej, jak na przykład func. Jeśli chcemy szukać miejsc zerowych funkcji, którą da się zapisać prostym wyrażeniem złożonym z operacji na dostępnych wielkościach i funkcjach możemy użyć jako argumentu wyrażenia lambda. Wyrażenie to zastępuje „pełną” definicję funkcji w momencie, gdy tak naprawdę taka pełna definicja nie jest nam potrzebna. W podanym przykładzie szukaną funkcję przekazaliśmy dwoma sposobami — raz z użyciem nazwy uprzednio zdefiniowanej funkcji func, a raz z użyciem wyrażenia lambda.
Drugim argumentem tej funkcji jest punkt startowy do poszukiwania miejsca zerowego. Powinniśmy najpierw zgrubnie oszacować położenie poszukiwanego miejsca zerowego i wpisać je tutaj. W zależności od funkcji parametr ten jest mniej lub bardziej istotny dla znalezienia poprawnego wyniku. Jest on zaś szczególnie istotny, jeśli badana funkcja ma więcej niż jedno miejsce zerowe (w tym przypadku wskazane może być wykreślenie funkcji).
Numeryczne obliczanie całek oznaczonych
- Przykład:
# -*- coding: utf-8 -*-
import scipy.integrate as si
import numpy as np
def func(x):
return x**3/(np.exp(x)-1)
print 'Całka od',0,'do',1,'wynosi',si.quad(func,0,1)
print 'Całka od',0,'do','+∞','wynosi',si.quad(func,0,np.inf)
print 'Całka od',0,'do','π','wynosi',si.quad(lambda x: np.sin(x),0,np.pi)
print 'Całka od',0,'do',1,'wynosi',si.quad(lambda x: x,0,1)
- Rezultat:
Całka od 0 do 1 wynosi (0.22480518802593821, 2.4958389580158414e-15)
Całka od 0 do +∞ wynosi (6.4939394022668298, 2.6284700289248249e-09)
Całka od 0 do π wynosi (2.0, 2.2204460492503131e-14)
Całka od 0 do 1 wynosi (0.5, 5.5511151231257827e-15)- Jak to działa?
Do numerycznego obliczania całek oznaczonych używamy funkcji quad z modułu scipy.integrate. Funkcja ta jako pierwszego argumentu wywołania oczekuje funkcji, którą będziemy całkować. Podobnie jak w poprzednim przykładzie, możemy tu przekazać nazwę funkcji osobno zdefiniowanej (func) albo wyrażenia lambda.
Drugi i trzeci argument funkcji quad to początek i koniec zakresu całkowania. Zauważ, że oprócz „normalnych” liczb możliwe są zakresy nieskończone, z użyciem stałej inf z modułu numpy. Rezultatem funkcji quad jest krotka dwuelementowa. Pierwszy jej element to wynik całkowania, natomiast drugi określa dokładność, z jaką udało się wynik ten policzyć.
Rozwiązywanie równań różniczkowych
- Przykład:
Rozwiązanie równania różniczkowego [math]\frac{dy(t)}{dt}=y[/math] z warunkiem początkowym [math]y(t=0)=1[/math].
import scipy.integrate as si
import numpy as np
import pylab as p
df = lambda y, t: y
X = np.linspace(0, 5, 51) # 51 punktów od 0 do 5 włącznie
wynik = si.odeint(df, 1, X)
p.plot(X, np.zeros_like(X), 'ro',
X, wynik, 'go',
X, numpy.exp(X), '--')
p.show()
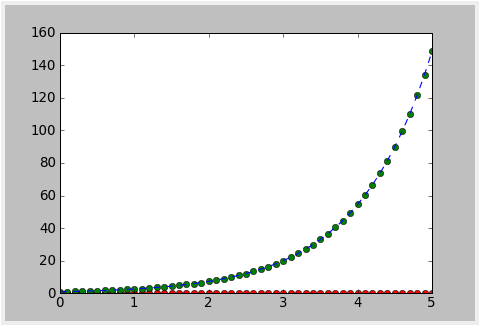
- Rezultat
- Jak to działa?
Poszukujemy funkcji [math]y(t)[/math] spełniającej nasze równanie różniczkowe [math]y^\prime=y[/math]. Funkcja odeint (skrót ODE pochodzi z angielskiego określenia ordinary differential equation czyli równanie różniczkowe zwyczajne) oblicza wartości poszukiwanej przez nas funkcji w punktach podanych jako jej trzeci argument.
Z teorii wiemy, że równanie to spełnia funkcja [math]y(t)=\exp(t)[/math] (spełnia je również funkcja [math]y(t) \equiv0 [/math], ale ze względu na przyjęty warunek początkowy ta funkcja nie może być naszym rozwiązaniem).
Równania wyższych stopni i układy równań różniczkowych
Poniższy przykład ilustruje jak można rozwiązać równanie różniczkowe zwyczajne wyższego rzędu. Jednocześnie będzie to przykład na rozwiązywanie układów równań różniczkowych.
Rozważmy masę [math]m[/math] umieszczoną na sprężynie o stałej sprężystości [math]k[/math]. Siła działająca na masę zależna jest od jej wychylenia [math]x[/math] z położenia równowagi i wynosi −kx. Równanie ruchu tej masy to (kropka nad symbolem zmiennej oznacza jej różniczkowanie po czasie: jedna kropka — pierwszą pochodną, dwie kropki — drugą pochodną):
- [math] m\ddot{x} = - k x [/math]
Dzieląc to równanie stronami przez [math]m[/math] otrzymujemy standardowe równanie oscylatora harmonicznego o częstości [math]\omega = \sqrt{\frac{k}{m}} [/math]:
- [math] \ddot{x} = - \omega^2 x [/math]
Funkcje całkujące równania różniczkowe w SciPy radzą sobie tylko z równaniami i układami równań pierwszego rzędu. Musimy zatem przepisać nasze równanie na układ równań pierwszego rzędu. Można to zrobić wprowadzając dodatkową zmienną. Tą zmienną jest [math]v = \dot{x}[/math] (prędkość masy). Teraz nasz układ wygląda tak:
- [math] \left\{ \begin{array}{l} \dot{x} = v \\ \dot{v} = - \omega^2 x \end{array} \right. [/math]
# -*- coding: utf-8 -*-
from scipy.integrate import odeint
import numpy as np
import pylab as p
def prawa_strona_rownania(w, t, params):
''' Argumenty:
w: wektor stanu (u nas x, v)
t: czas
params: wektor parametrów (u nas omega_kwadrat)
W wektorze f funkcja zwraca
obliczone dla danego wektora stanu
wartości prawej strony równania
'''
x, v = w # dla czytelności równania wypakowuję zmienne z wektora "w"
omega_kwadrat, = params # i podobnie z parametrami "params"
# poniżej do tablicy f w kolejnych wierszach wpisuję
# kolejne prawe strony równań stanowiących układ
f = [v, # wartość pochodnej dx/dt
-omega_kwadrat * x] # wartość pochodnej dv/dt
return f
t = np.linspace(0, 5, 51)
params = [2]
w = [0, 3] # warunek początkowy (t=0) dla x i v
print "Wektor stanu w chwili początkowej: ",
print prawa_strona_rownania(w, t[0], params)
# argumentami odeint są:
# - nazwa funkcji,
# - wektor stanu początkowego,
# - wektor zawierający chwile czasu, dla których ma być zwrócony stan układu
# - krotka zawierająca dodatkowe parametry, które mają być przekazane do funkcji
# opisującej prawe strony równań
wynik = odeint(prawa_strona_rownania, w, t, args=(params,) )
x = wynik[:, 0]
v = wynik[:, 1]
p.plot(t,x, t,v)
p.legend(('x', 'v'))
p.grid(True)
p.show()
Funkcja odeint oczekuje przynajmniej trzech parametrów: funkcji obliczającej pochodną poszukiwanej funkcji (albo pochodne poszukiwanych funkcji w przypadku układu równań), warunku początkowego dla szukanych funkcji oraz sekwencji punktów czasu, w których będzie obliczone rozwiązanie. W naszym przypadku będą to:
- nazwa funkcji obliczającej pochodne — prawa_strona_rownania, zwraca wektor [math][\dot{x},\ \dot{v}][/math], czyli [math][v,\ -\omega ^2 x][/math];
- warunek początkowy — lista w = [0, 3], czyli [x(0), v(0)];
- sekwencja punktów czasu — wektor t = np.linspace(0,5,51), czyli [0, 0,1, 0,2,... 4,9, 5].
U nas jest jeszcze czwarty parametr (nazwany, o nazwie args). Powinna być to krotka zawierająca dodatkowe parametry, jakich może potrzebować funkcja obliczająca wartości pochodnych. U nas jest taki jeden dodatkowy parametr: ω2, która w naszym programie jest przechowywana w zmiennej params. Tworzymy więc z niej krotkę jednoelementową i przekazujemy ją funkcji odeint jako czwarty parametr. Zostanie ona użyta podczas liczenia prawej strony równań rozwiązywanego układu, czyli w funkcji prawa_strona_rownania.
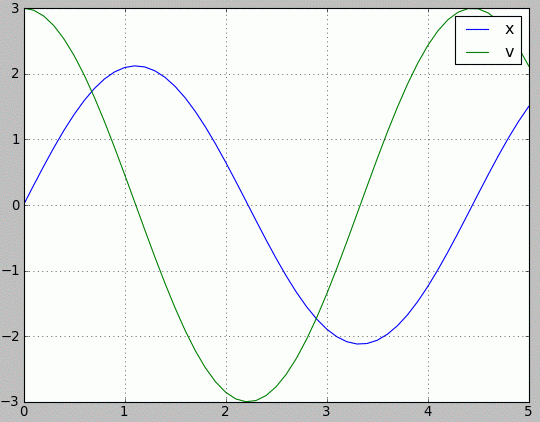
- Rezultat
Otrzymujemy wykres zmiennych x i v czyli położenia i prędkości masy zaczepionej na sprężynie. Ponieważ zastosowaliśmy warunek początkowy x(0) = 0, v(0) = 3, więc w chwili początkowej masa mija punkt równowagi x=0 z prędkością 3 jednostek. Otrzymujemy drgania z amplitudą teoretycznie 3/ω = 2,12 jednostek.
Transformata Fouriera
import pylab as p
import numpy as np
import scipy.fftpack as sf
x = np.loadtxt('c4spin.txt')
p.subplot(2,1,1)
p.plot(x)
p.subplot(2,1,2)
z=sf.fft(x)
widmo = np.abs(z[:len(z)/2])
p.plot(widmo)
p.show()
http://brain.fuw.edu.pl/~jarek/SYGNALY/TF/c4spin.txt
- Rezultat
Jak to działa
Moduł scipy.fftpack dostarcza narzędzi do liczenia transformaty Fouriera. Transformata Fouriera pozwala wyznaczyć skład częstotliwościowy sygnału. W powyższym przykładzie wczytujemy dane z pliku tekstowego poleceniem np.loadtxt('c4spin.txt'). Dane te interpretujemy jako kolejne próbki pewnego sygnału.
Na górnym panelu rysunku wykreślamy przebieg sygnału w czasie. Funkcja sf.fft(x) oblicza transformatę Fouriera sygnału x. Zmienna z zawiera pełną informację o transformacie Fouriera sygnału x — jest to wektor liczb zespolonych. Aby uzyskać informację o częstościach zawartych w sygnale x trzeba wziąć wartość bezwzględną liczb z. Jeśli ponadto sygnał x składa się z liczb rzeczywistych (a tak jest w naszym przypadku) to wynikowy wektor z zawiera pełną informację o składzie częstotliwościowym w swojej pierwszej połowie. Dlatego do zmiennej widmo przepisujemy tylko wycinek z[:len(z)/2]. Na dolnym panelu wyrysowujemy zmienną widmo.