Uczenie maszynowe i sztuczne sieci neuronowe/Wykład 5
Spis treści
Na poprzednim wykładzie
wyprowadziliśmy metodę uczenia wielowarstwowych sieci nieliniowych bazującą na minimalizacji funkcji kosztu metodą gradientową. W dzisiejszym wykładzie zastanowimy się jak robić to w sposób:
- szybszy
- zmniejszający ryzyko wpadania w minima lokalne
- prowadzący do lepszej generalizacji
Przyspieszanie uczenia
Bezwładność
Podobnie jak dla sieci liniowej przyspieszenie uczenia można uzyskać poprzez dodanie członu bezwładności do formuły zmiany wag:
- [math]\Delta w^{(j+1)} = - \alpha_1 \frac{\partial J}{\partial w} + \alpha_2\Delta w^{(j)} [/math]
Dla prawie płaskiej powierzchni kosztu efektywny współczynnik uczenia jest [math] \frac{1}{1-\alpha_2}[/math] razy większy niż w przypadku algorytmu bez bezwładności. Dla typowych wartości [math]\alpha_1 = 0.1[/math] i [math]\alpha_2 = 0.9[/math] otrzymujemy około 10 krotne przyspieszenie!
Adaptacyjny dobór parametrów
Kiedy obserwujemy proces minimalizacji funkcji błędu to często widać, że stała wartość parametru uczenia [math]\alpha_1[/math] nie jest optymalna. Czasami widać, że funkcja długi czas maleje prawie monotonicznie - wtedy lepiej byłoby mieć większą wartość [math]\alpha_1[/math], kiedy indziej bardzo oscyluje - to świadczy o zbyt dużej wartości [math]\alpha_1[/math].
Prosty pomysł
Jednym z prostych pomysłów na zautomatyzowanie procesu dobierania wartości [math]\alpha_1[/math] jest następujący schemat zmiany tego parametru:
- [math] \Delta \alpha_1 = \left\{ \begin{array}{lcl} + a& \text{dla} & \Delta J \lt 0 \\ -b \alpha_1 & \text{dla} & \Delta J \gt 0 \\ 0 & \text{dla pozostalych przypadkow} \end{array} \right. [/math]
Po wykonaniu kroku prowadzącego do zwiększenia funkcji kosztu warto go wycofać.
Elastyczna wsteczna propagacja błędu
Resilient Backpropagation — do zmiany wag wykorzystujemy jedynie informację o znaku gradientu. W poniższych formułach [math]w_q^p[/math] to waga łącząca wyjście neuronu q z odpowiednim (q-tym) wejściem neuronu p.
- [math] \Delta w_q^{p(j)} = - \text{sign} \left(\frac{\partial J}{\partial w_p^q}\right) \Delta_q^{p(j)} [/math]
gdzie: [math]J[/math] jest miarą błędu po prezentacji wszystkich bodźców, zaś [math]\Delta_q^{p(j)}[/math]:
- [math] \Delta_q^{p(j)} = \left\{ \begin{array}{lcl} \eta^+ \Delta_q^{p(j-1)} & \text{dla} & \frac{\partial J^{(j-1)}}{\partial w_p^q}\frac{\partial J^{(j)}}{\partial w_p^q} \gt 0 \\ \eta^- \Delta_q^{p(j-1)} & \text{dla} & \frac{\partial J^{(j-1)}}{\partial w_p^q}\frac{\partial J^{(j)}}{\partial w_p^q} \lt 0 \\ \Delta_q^{p(j-1)} & \text{dla pozostalych przypadkow} \end{array} \right. [/math]
gdzie: [math] 0 \lt \eta^- \lt 1 \lt \eta^+[/math]. Dodatkowo ustala się ograniczenie na możliwe wartości [math] \Delta_{min} \lt \Delta_p^q \lt \Delta_{max}[/math]. Standardowo [math]\Delta_{min} \approx 10^{-6}[/math] a [math] \Delta_{max} \approx 50[/math].
Dla sigmoidalnych funkcji odpowiedzi metoda ta może poprawić uczenie w obszarze ogonów sigmoidy, gdzie wartość gradientu jest bardzo mała.
Metoda najszybszego spadku
Kolejnej wartości wagi szukamy wzdłuż prostej wyznaczonej przez poprzedni wektor wag [math]w^{(j)}[/math] i kierunek [math]d^{(j)}[/math], zmieniając [math]\lambda[/math] tak, aby zminimalizować w danym kierunku [math]J[/math]:
- [math]w^{(j+1)} = w^{(j)} + \lambda d^{(j)}[/math]
Kierunek [math]d[/math] wybieramy przeciwnie do gradientu [math]J[/math]
- [math] d^{(j)} = -\nabla J(w^{(j)})[/math]
Zauważmy, że stary i nowy kierunek minimalizacji są ortogonalne, bo lambda jest dobrana tak, aby minimalizować funkcję kosztu w kierunku [math]d^{(j)}[/math] tzn.:
- [math]\frac{\partial}{\partial \lambda} J(w^{(j)} + \lambda d^{(j)}) = 0 [/math]
Ale rozwijając powyższy wzór widzimy, że:
- [math]\frac{\partial}{\partial \lambda} J(w^{(j)} + \lambda d^{(j)}) = \frac{\partial J\left(w^{(j+1)}\right)}{\partial w} \frac{\partial (w^{(j)}+ \lambda d^{(j)})}{\partial\lambda} = \nabla J(w^{(j+1)}) \cdot d^{(j)} = -d^{(j+1)} \cdot d^{(j)} =0 [/math]
Metoda gradientu sprzężonego
Poprzednią metodę można udoskonalić przez rezygnację z ortogonalności kolejnych kroków:
- [math]d^{(j+1)} = -\nabla J \left( w^{(j+1)} \right) + \beta d^{(j)}[/math]
i trzeba chytrze dobrać [math]\beta[/math] tak, aby jak najmniej psuć efekt osiągnięty w poprzednim kroku. Nowy kierunek szukania powinien więc być taki, aby z dokładnością pierwszego rzędu nie zmieniał składowej gradientu, która w poprzednim kroku została wyzerowana. A zatem chcemy, aby z dokładnością do wyrazów pierwszego stopnia, spełnione było:
- [math] d^{(j)} \cdot \nabla J\left( w^{(j)} + \lambda d^{(j+1)} \right) = 0 [/math]
praktyczny sposób na znalezienie [math] \beta[/math] spełniającego powyższy warunek podaje reguła Polaka-Ribiere‘a:
- [math] \beta = \frac{\left( \nabla J\left (w^{(j+1)} \right) - \nabla J \left( w^{(j)}\right)\right) \cdot \nabla J\left(w^{(j+1)}\right)}{ \left( \nabla J \left(w^{(j)}\right)\right)^2}[/math]
Metody quasi-Newtona
Oryginalna metoda Newtona polega na minimalizacji funkcji kosztu z wykorzystaniem drugich pochodnych. Rozwijając [math]J(w)[/math] wokół bieżącego wektora wag [math]w_0[/math] mamy:
- [math]J(w)=J(w_0)+(w-w_0)\cdot \nabla J\left( w_0\right) + \frac{1}{2} (w - w_0) \cdot H \cdot(w - w_0) +... [/math] (∗)
gdzie: H to hesjan (macierz drugich pochodnych cząstkowych [math] H_{ij} =\frac{\partial^2 J}{\partial w_i \partial w_j}[/math] ).
Różniczkowanie (*) daje:
- [math] \nabla J(w) = \nabla J(w_0) + H \cdot (w - w_0) + \dots[/math]
chcemy znaleźć minimum [math]J[/math] czyli spełnić warunek [math] \nabla J(w) = 0[/math]:
- [math] \nabla J(w_0) + H \cdot (w - w_0) = 0[/math]
stąd:
- [math]w = w_0 + H^{-1} \nabla J \left(w_0 \right) [/math]
Wzór ten można stosować iteracyjnie. Metoda w oryginalnej postaci jest bardzo kosztowna obliczeniowo ([math]O(n^3)[/math]) i jest niestabilna numerycznie. Stąd też realne implementacje są nieco inne i zasadniczo polegają na iteracyjnej aktualizacji hesjanu. Zwykle wymaga mniej kroków niż metoda gradientów sprzężonych, ale w każdym kroku jest więcej obliczeń i trzeba mieć pamięć na przechowywanie hesjanu.
Algorytm Lavenberg-Marquardt'a
Metoda ta korzysta z faktu, że hesjan może być przybliżony przez:
- [math] \mathbf{H} \approx \mathbf{J}^T \mathbf{J}[/math]
gdzie: [math]\mathbf{J}[/math] — macierz jakobiego (macierz pierwszych pochodnych cząskowych) natomiast
- [math]\nabla J \left(w^{(j)}\right) = \mathbf{J}^T (z^{(j)} - y^{(j)})[/math]
W metodzie tej wagi zmieniamy:
- [math]w^{(j+1)} = w^{(j)} + [\mathbf{J}^T\mathbf{ J} + \mu \mathbf{I}]^{-1} \mathbf{J}^T (z^{(j)} - y^{(j)})[/math]
dla [math] \mu = 0[/math] jest to metoda Newtona z przybliżoną wartością hesjanu, dla [math] \mu[/math] dużego metoda dąży do zwykłej metody gradientowej. Metoda Newtona jest szybsza i dokładniejsza w pobliżu minimum [math]J[/math].
[math] \mu[/math] jest zmniejszane po każdym udanym kroku a zwiększane jeśli w danym kroku [math]J[/math] wzrosło.
Podsumowanie metod przyspieszania uczenia
- Ogólnie
- Za szybkość płacimy ilością koniecznej pamięci i wymaganą precyzją obliczeń
- Algorytm Lavenberg-Marquardt'a
- jest najszybszym algorytmem w problemach aproksymacji funkcji dla sieci o średniej wielkości (do kilkuset wag). Prowadzi też, na ogół, w tych problemach do lepszego dopasowania w sensie błędu średniokwadratowego od pozostałych algorytmów. Jest jednak kosztowny jeśli chodzi o zapotrzebowanie na pamięć.
- Resilient Backpropagation
- wydaje się być najlepszy w problemach rozpoznawania wzorców, ale nie nadaje się w zasadzie do aproksymacji funkcji. Nie jest pamięciożerny.
- Algorytm gradientów sprzężonych
- jest najbardziej uniwersalnym algorytmem. Ma umiarkowane wymagania co do ilości pamięci.
- Zwykła metoda gradientowa
- jest najwolniejsza, ale może to być użyteczne jeśli bardziej niż na czasie zależy nam na generalizacji.
Problem minimów lokalnych
Wszystkie metody minimalizacji funkcji kosztu mogą utknąć w minimach lokalnych. Kilka metod, które mogą pomóc zmniejszyć problemy z minimami lokalnymi:
- uniknięcie wysycenia sigmoid już na samym początku uczenia. Np. dla unormowanego wejścia i dla sigmoidy z [math]\beta = 1 [/math] wybranie początkowych wag losowych o takich wartościach, że średnie pobudzenie neuronu e jest mniejsze, ale nie za bardzo niż 1 (można losować wagi rzędu [math]\sqrt \frac{1}{k_i}[/math] gdzie [math]k_i[/math] ilość wejść do jednostki i);
- poprawianie wag po każdej prezentacji wzorca, przy czym wzorce prezentowane są w losowej kolejności;
- zastosowanie jednostek stochastycznych — gradient oraz dodatkowy parametr T temperatura kontrolują prawdopodobieństwo zmiany wagi w określonym kierunku;
- delikatne losowe zmiany wag;
- przy każdej prezentacji wzorca dodawanie do niego troszkę szumu. Dodanie szumu zawsze spowolni proces uczenia, przy czym mała dawka może pomóc uniknąć minimów lokalnych, duża - znacznie spowalnia uczenie.
Twierdzenie o potencjalnych możliwościach sieci
Sieć nieliniowa co najmniej dwuwarstwowa może aproksymować dowolną funkcję swoich wejść, ze z góry zadaną dokładnością. Konieczna jest jedynie dostatecznie duża ilość jednostek w warstwach ukrytych. Do aproksymacji dowolnej funkcji ciągłej wystarcza jedna warstwa ukryta.
Uzasadnienie nieformalne:
- Każda “rozsądna” funkcja [math] F_i{X_k}[/math] może być przedstawiona jako liniowa kombinacja “wypukłości”, z których każda jest różna od zera tylko w pobliżu [math]X_k[/math].
- Takie “wypukłości” można skonstruować z dwóch warstw ukrytych.
Gdzie jest problem?
- twierdzenie mówi jedynie o istnieniu rozwiązania
- w ogólności nie wiadomo ile jednostek w warstwach stanowi “dostatecznie dużą ilość”
- nie ma gwarancji, że problem da się rozwiązać metodą wstecznej propagacji błędu, tzn. że dotrzemy do minimum globalnego funkcji kosztu.
- Trywialne twierdzenie
- uczenie sieci zawsze się uda jeśli zastosujemy prawidłowy preprocesor.
Jeśli w problemie występują symetrie, to o ile to możliwe warto przenieść ich analizę do fazy preprocesingu, bo powodują one powstanie w funkcji kosztu okresowości, wielokrotnych minimów lokalnych, płaskich dolin i wyżyn.
Ze standardowych technik przygotowywania danych (nie tylko dla sieci nuropodobnych) warto rozważyć:
- wyskalowanie danych,
- normalizację danych,
- przeprowadzenie analizy składowych głównych.
Generalizacja
O co tu chodzi?
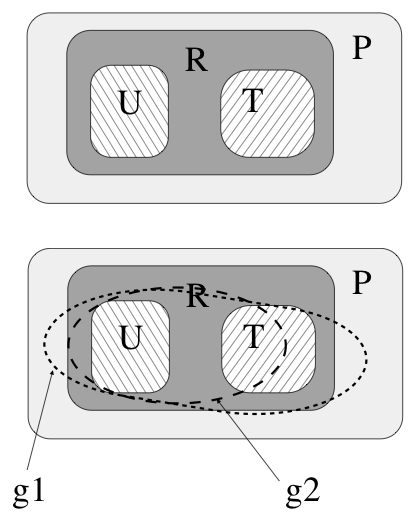
Na rysunku obok przedstawiona jest schematycznie koncepcja generalizacji. Wyobraźmy sobie, że jest pewna przestrzeń P, która zawiera pary, np. liczb {((a,b), c)}. W tym przykładzie jest to przestrzeń wszystkich odwzorowań [math]\mathcal{R}^2 \rightarrow \mathcal{R}[/math]. Niektóre z tych par reprezentują pewną konkretną relację R: np. są to pary spełniające warunek [math]c=\sqrt{a^2 +b^2}[/math]. Wyobraźmy sobie dalej, że mamy dane dwa skończone zestawy par, które tą relację spełniają, ale oczywiście nie są w stanie obejmować wszystkich możliwych par. Jeden z nich oznaczymy U, a drugi T. Załóżmy, że mamy dwie wersje sieci, które uczymy na zbiorze U (mogą się one różnić architekturą, albo punktem startu procedury uczącej, albo ilością iteracji algorytmu uczącego itp.). Po procesie uczenia sieci te mają mały i porównywalny błąd na zbiorze U, ale jedna z nich nauczyła się relacji wskazanej na rys. jako g1 a druga relacji g2. Na podstawie rezultatów odtwarzania przykładów ze zbioru testowego mówimy, że sieć druga ma lepszą generalizację niż sieć pierwsza.
Jakie mogą być przyczyny złej generalizacji?
Architektura nie wystarczająca do reprezentacji relacji
Architektura zbyt złożona ...
... do danego odwzorowania i zbyt długi proces uczenia:
- Dotyczy to sytuacji, gdy zbiór uczący zawiera przykłady danej relacji z szumem. Sieć ma tak dużo parametrów, że jest w stanie nauczyć się szczegółów zbioru uczącego nie związanych z interesującą nas relacją. Zjawisko takie nazywamy przeuczeniem.
Uczenie z kryterium wczesnego stopu
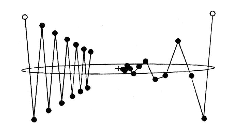
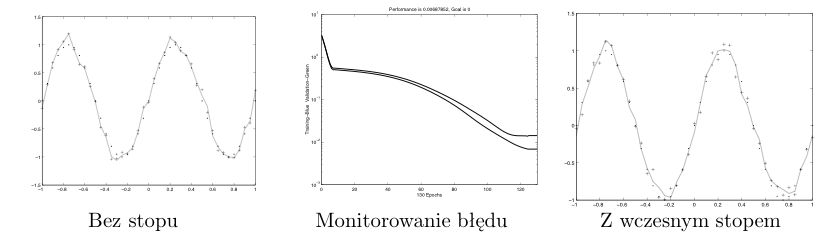
Prostym rozwiązaniem jest w takim przypadku uczenie z kryterium wczesnego stopu. Polega ono na tym, że oprócz zbioru uczącego posiadamy rozłączny z nim zbiór testowy. W trakcie uczenia obliczamy błąd popełniany przez sieć na zbiorze uczącym i na zbiorze testowym. W większości przypadków powinniśmy w początkowej fazie uczenia obserwować malenie błędu na obu zbiorach. Oczekujemy, że w pewnym momencie, kiedy sieć zaczyna się uczyć zbędnych szczegółów to błąd na zbiorze uczącym będzie nadal malał, a na zbiorze testowym zacznie rosnąć. Uczenie prowadzimy tylko do momentu, kiedy błąd na obu zbiorach maleje. Przykład takiej procedury pokazany jest na poniższym rysunku.
Optymalizacja architektury: Regularyzacja
- Pomysł
- zacznijmy od dużej sieci i po pewnym cyklu uczenia przeanalizujmy połączenia w sieci usuwając mało istotne połączenia lub jednostki. Następnie powtórzmy uczenie.
Można spróbować tak zmodyfikować regułę zmiany wag, aby połączenia nieistotne same dążyły do 0; po standardowym kroku uczenia zmniejszamy wagi:
- [math] w_q^{p(j+1)} = (1- \epsilon) w_q^{p(j)} [/math] (*)
Jest to równoważne modyfikacji funkcji kosztu:
- [math]J = J_0 + \frac{1}{2} \gamma \sum_{pq}\left(w_q^p \right)^2[/math]
przy [math]\epsilon = \alpha \gamma[/math].
Konsekwencje:
- rozwiązanie jest “gładsze”
- wygładzenie funkcji kosztu likwiduje część minimów lokalnych
Powyższa funkcja kosztu prowadzi do preferowania większej liczby małych wag zamiast jednej dużej. Sytuację poprawia wyrażenie:
- [math] J = J_0 +\frac{1}{2}\gamma \sum_{pq} \frac{\left(w_q^p\right)^2}{1+\left(w_q^p \right)^2}[/math]
co jest równoważne (*) przy
- [math]\epsilon_q^p = \frac{\alpha \gamma}{\left( 1+ \left(w_q^p \right)^2\right)^2}[/math].
Dzięki temu małe wagi zanikają szybciej niż duże. To załatwia problem zanikania niepotrzebnych połączeń.
Aby zautomatyzować usuwanie zbędnych jednostek możemy zastosować:
- [math] \epsilon^p = \frac{\alpha \gamma}{ \left( 1+\sum_q \left( w_q^p \right)^2\right)^2}[/math]
dla wszystkich wejść do jednostki p.
Powoduje to szybsze zanikanie wag dla jednostek, które mają małe wagi wejściowe.
Diagnostyka i debugowanie algorytmu uczącego
Załóżmy, że zaimplementowaliśmy algorytm uczący na określonym (niewielkim) zbiorze danych. Mamy 20 % błędnych decyzji. Co z tym robić dalej?
Potencjalnie można:
- poprawić algorytm
- zdobyć więcej przykładów do ciągu uczącego
- wypróbować więcej cech lub ograniczyć przestrzeń cech
- pouczyć dłużej albo zmienić algorytm optymalizacyjny
- zmienić parametry uczenia (współczynnik szybkości, regularyzacji, itp.)
Każda z tych metod naprawia jakiś (ale inny) problem.
Aby zdiagnozować problem dobrze jest analizować wykresy:
- błędu od długości uczenia
- czy algorytm jest zbieżny? -> jeśli nie to możemy próbować poprawić to zmniejszając prędkość uczenia lub zmieniając procedurę optymalizacyjną
- błędu od rozmiaru zbioru uczącego
- Jeśli błąd na zbiorze uczącym dużo niższy niż na testowym to możemy mieć problem przeuczenia
- można: dodać przykładów, zmniejszyć rozmiar wejścia, włączyć regularyzację
- Duży błąd na zbiorze uczącym i na testowym -> źle dobrane cechy lub struktura klasyfikatora
- zmienić zestaw cech
- wzbogacić strukturę klasyfikatora (np. więcej jednostek ukrytych)
- Jeśli błąd na zbiorze uczącym dużo niższy niż na testowym to możemy mieć problem przeuczenia