Filtry: Różnice pomiędzy wersjami
| Linia 167: | Linia 167: | ||
</math> | </math> | ||
| + | dlatego taki filtr nazwać można filtrem rekursywnym, autoregresyjnym (AR), lub | ||
| + | filtrem o nieskończonej odpowiedzi impulsowej (Infinite Impulse Response IIR), bo potencjalnie raz wzbudzony (sekwencją jednostkową) może dowolnie długo produkować niezerowe wyjście. | ||
| + | Faza filtrowanego sygnału zaburzana jest nieliniowo ('''nonlinear phase filter''') | ||
| − | + | Filtry IIR mogą być też implementowane jako połączenie członów AR i MA, czyli: | |
| − | |||
| − | |||
::<math> | ::<math> | ||
| Linia 178: | Linia 179: | ||
\end{array} | \end{array} | ||
</math> | </math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Liniowe i nieliniowe przesunięcie fazy== | ==Liniowe i nieliniowe przesunięcie fazy== | ||
Wersja z 15:00, 22 lip 2024
Spis treści
AS/ Funkcja przejścia i filtry
Cyfrowe filtry liniowe niezmiennicze w czasie [math]x[n] \longrightarrow \boxed{LTI} \longrightarrow y[n][/math] opisuje liniowe równanie różnicowe o stałych współczynnikach
- [math] \displaystyle y[n] = \sum_{k=1}^K a_k y[n-k] + \sum_{l=0}^L b_l x[n-l] [/math]
gdzie [math]a_i[/math] i [math]b_i[/math] to współczynniki, [math]x[n][/math] to sygnał wejściowy, a [math]y[n][/math] — wyjście; w ogólniejszej postaci można je zapisać jako
- [math] \displaystyle \sum_{k=0}^K a_k y[n-k] = \sum_{l=0}^L b_l x[n-l] [/math]
Funkcja przejścia (transfer function)
Stosując transformatę [math]Z[/math] możemy powyższe równanie z dziedziny czasu przenieść do dziedziny częstości:
- [math] \displaystyle \mathcal{Z}\left\{\sum_{k=0}^K a_k y[n-k] \right\} = \mathcal{Z}\left\{ \sum_{l=0}^L b_l x[n-l] \right\} [/math]
- [math] \displaystyle \sum_{k=0}^K a_k \mathcal{Z}\left\{ y[n-k]\right\} = \sum_{l=0}^L b_l \mathcal{Z} \left\{x[n-l]\right\} [/math]
- [math] \displaystyle \sum_{k=0}^K a_k z^{-k} Y(z) = \sum_{l=0}^L b_l z^{-l} X(z) [/math]
- [math] \displaystyle Y(z) \sum_{k=0}^K a_k z^{-k} = X(z) \sum_{l=0}^L b_l z^{-l} [/math]
Dla systemu przyczynowego dostajemy:
- [math] \displaystyle \frac{Y(z)}{X(z)} \equiv H(z) = \frac{\sum_{l=0}^L b_l z^{-l}}{\sum_{k=0}^K a_k z^{-k}} [/math]
Filtry
Funkcja przejścia [math]H(z)[/math] pozwala spójnie przedstawić działanie filtra LTI na sygnał [math]x[/math] w przestrzeni transformaty [math]\mathcal{Z}[/math]:
- [math] \displaystyle Y(z)=H(z)X(z)=\frac{b_0 + b_1 z^{-1}+\dots +b_{L} z^{-L}}{a_0+a_1 z^{-1}+\dots +a_{K} z^{-K}}X[z] [/math]
gdzie [math]X(z)[/math] to transformata [math]\mathcal{Z}[/math] filtrowanego sygnału (wejścia), [math]Y(z)[/math] — wyjścia, a [math]H(z)[/math] to wprowadzona powyżej funkcja przejścia filtra. Filtrowanie w przestrzeni transformaty Z odpowiada przemnożeniu transformaty sygnału przez transformatę funkcji przejścia filtru. Zobaczmy, co się stanie z widmem sygnału po przefiltrowaniu.
Weźmy w tym celu [math]z = e^{i\omega}[/math]. Wówczas transmitancja jest funkcją częstości [math]\omega[/math]. Konkretnej częstości [math]\omega_k[/math] przypisuje ona liczbę zespoloną, którą można wyrazić jako [math]A_k e^{i \phi_k}[/math].
- [math] \displaystyle Y[e^{i\omega}]=H[e^{i\omega}]X[e^{i\omega}]=\frac{b_0+b_1 e^{-i\omega}+\dots +b_L e^{-i L\omega}}{a_0+a_1 e^{-i\omega}+\dots +a_K e^{-i K\omega}}X[e^{i\omega}] [/math]
W dziedzinie częstości sygnał wyrażony jest przez współczynniki Fourierowskie. Dla konkretnej częstości współczynnik taki [math]X_k = |X_k| e^{i \theta_k}[/math] (liczba zespolona) mówi z jaką amplitudą i jaką fazą exponens zespolony o danej częstości ([math]z_k = e^{i\omega_k}[/math]) wchodzi w skład sygnału.
Działanie filtru na sygnał w dziedzinie częstości polega na przemnożeniu składowej sygnału o częstości [math]f_k[/math] przez liczbę [math]A_k e^{i \phi_k}[/math]:
- [math]Y(f_k) = A_k e^{i \phi_k} |X_k| e^{i \theta_k} = A_k |X_k| e^{i ( \phi_k +\theta_k)} e^{i 2\pi f_k} [/math]
W wyniku filtrowania sinusoidalna składowa sygnału o danej częstości może zmienić amplitudę i fazę, ale nie zmienia częstości. Zera i bieguny filtra to odpowiednio miejsca zerowe licznika i mianownika funkcji przenoszenia.
Finite Impulse Response (FIR) — filtr o skończonej odpowiedzi impulsowej
Jeśli w równaniu
- [math] \displaystyle \sum_{k=0}^K a_k y[n-k] = \sum_{l=0}^L b_l x[n-l] [/math]
położymy [math]a_i = 0[/math] poza [math]a_0=1[/math], dostaniemy
- [math] \displaystyle y[n] = \sum_{l=0}^L b_l x[n-l] [/math]
W funkcji przejścia mianownik będzie stały i dostaniemy
[math] \displaystyle Y[z]=H[z]X[z]=\left(b_0+b_1 z^{-1}+\dots +b_L z^{-L}\right) X[z] [/math]
a w dziedzienie czasu, z pełnego równania
- [math] \displaystyle y[n] = b_0 x[n]+ b_1 x[n-1] + \dots + b_L x[n-L] \,\,\, - \,\,\, a_1 y[n-1] - \dots - a_K y[n-K] [/math]
pozostaje
- [math] \displaystyle y(n) = b_0 *x[n] + b_1 *x[n-1] + \dots + b_L *x[n-L] [/math]
Jeśli współczynniki [math]b_i[/math] zapiszemy jako sekwencję [math]b[i][/math], działanie takiego filtra LTI na sygnał [math]x[n][/math] w dziedzinie czasu będze wyglądała tak:
- [math] \displaystyle y(n) = b[0]*x[n] + b[1]*x[n-1] + \dots + b[L]*x[n-L] = b[n]*x[n] [/math]
Taki filtr nazywamy filtrem o skończonej odpowiedzi impulsowej (Finite Impulse Response, FIR), bo odpowiedź na impuls kończy się po [math]L[/math] próbkach. Inna nazwa to średnia biegnąca (Moving Average, MA).
Infinite Impulse Response (IIR) — filtr o nieskończonej odpowiedzi impulsowej
Jeśli w równaniu
- [math] \displaystyle \sum_{k=0}^K a_k y[n-k] = \sum_{l=0}^L b_l x[n-l] [/math]
położymy [math]b_i = 0[/math] poza [math]b_0=1[/math], dostaniemy
- [math] \displaystyle \sum_{k=0}^K a_k y[n-k] = x[n] [/math]
w funkcji przejścia licznik będzie stały
- [math] \displaystyle Y[z]=H[z]X[z]=\frac{1}{a_0+a_1 z^{-1}+\dots +a_{K} z^{-K}}X[z] [/math]
Operacja splotu działa tu na sekwencji wyjściowej:
- [math] y[n] = x[n] - a[1]*y[n-1] - \dots - a[n_a]*y[n-K] [/math]
dlatego taki filtr nazwać można filtrem rekursywnym, autoregresyjnym (AR), lub filtrem o nieskończonej odpowiedzi impulsowej (Infinite Impulse Response IIR), bo potencjalnie raz wzbudzony (sekwencją jednostkową) może dowolnie długo produkować niezerowe wyjście. Faza filtrowanego sygnału zaburzana jest nieliniowo (nonlinear phase filter)
Filtry IIR mogą być też implementowane jako połączenie członów AR i MA, czyli:
- [math] \begin{array}{ll} y[n] = b[0]*x[n] &+ b[1]*x[n-1] + \dots + b[L]*x[n-L]\\ &- a[1]*y[n-1] - \dots - a[K]*y[n-K] \end{array} [/math]
Liniowe i nieliniowe przesunięcie fazy
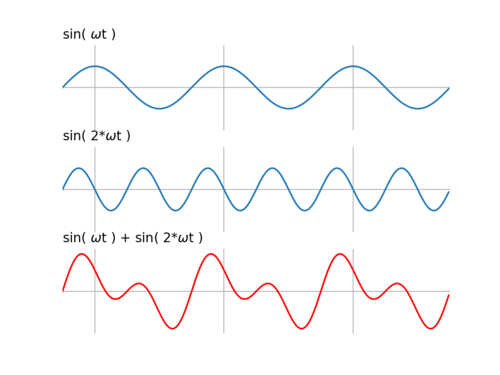
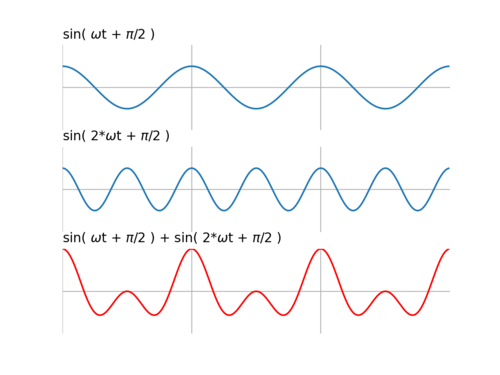
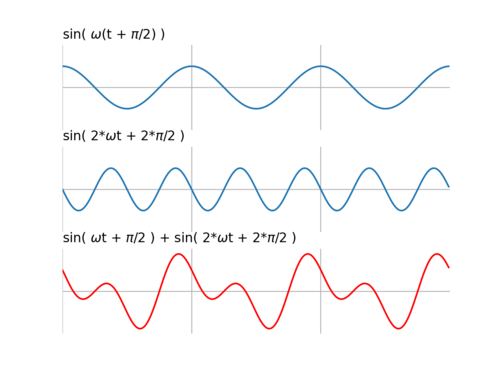
Jeśli współczynniki filtra FIR tworzą sekwencję symetryczną bądź antysymetryczną, oparty na nich filtr o skończonej odpowiedzi impulsowej będzie liniowo przesuwał fazę filtrowanego sygnału (linear phase filter) — cały sygnał skutkiem filtrowania jest przesunięty w czasie o ok. połowę długości filtra FIR.
Rzędem filtru nazywamy maksymalne opóźnienie w próbkach potrzebne do wytworzenia nowej próbki wyjściowej. Dla filtrów FIR jest on równy liczbie [math]L[/math]. Dla filtrów IIR jest to większa z liczb [math]L, K[/math].
| kod (uproszczony) |
import matplotlib.pyplot as plt
import numpy as np
t = np.arange(0.0, 3, 0.01)
s1 = np.sin(2 * np.pi * t)
s2= np.sin(2 * np.pi * t + np.pi/2)
s3= np.sin(2*2 * np.pi * t)
s4= np.sin(2*2 * np.pi * t + np.pi/2)
s5= np.sin(2*2 * np.pi * t + 2*np.pi/2)
fig1, ax1 = plt.subplots(3, 1)
ax1[0].plot(t, s1)
ax1[1].plot(t, s3)
ax1[2].plot(t, s1+s3, 'r')
ax1[0].set_title('sin(wt)')
ax1[1].set_title('sin(2wt)')
ax1[2].set_title('sin(wt) + sin(2wt)')
fig2, ax2 = plt.subplots(3, 1)
ax2[0].plot(t, s2)
ax2[1].plot(t, s4)
ax2[2].plot(t, s2+s4, 'r')
ax2[0].set_title('sin(wt+pi/2)')
ax2[1].set_title('sin(2wt+pi/2)')
ax2[2].set_title('sin(wt+pi/2) + sin(2wt+pi/2)')
fig3, ax3 = plt.subplots(3, 1)
ax3[0].plot(t, s2)
ax3[1].plot(t, s5)
ax3[2].plot(t, s2+s5, 'r')
ax3[0].set_title('sin(w(t+pi/2))')
ax3[1].set_title('sin(2wt+2*pi/2)')
ax3[2].set_title('sin(wt+pi/2) + sin(2wt+2*pi/2)')
plt.show()
|
| kod generujący obrazki |
import matplotlib.pyplot as plt
import numpy as np
t = np.arange(0.0, 3, 0.01)
s1 = np.sin(2 * np.pi * t)
s2 = np.sin(2 * np.pi * t + np.pi / 2)
s3 = np.sin(2 * 2 * np.pi * t)
s4 = np.sin(2 * 2 * np.pi * t + np.pi / 2)
s5 = np.sin(2 * 2 * np.pi * t + 2 * np.pi / 2)
def fix_axes():
for i in range(0, 3):
ax[i].set_yticks([0], [])
ax[i].set_xlim([0, 3])
ax[i].grid(True)
ax[i].set_frame_on(False)
ax[i].tick_params(length=0)
ax[i].set_ylim(-2, 2)
fig1, ax = plt.subplots(3, 1, dpi=200)
ax[0].plot(t, s1)
ax[1].plot(t, s3)
ax[2].plot(t, s1 + s3, 'r')
ax[0].set_title('sin( $\omega$t )', loc='left')
ax[1].set_title('sin( 2*$\omega$t )', loc='left')
ax[2].set_title('sin( $\omega$t ) + sin( 2*$\omega$t )', loc='left')
fix_axes()
for i in range(0, 3):
ax[i].set_xticks(np.arange(.25, 3, 1), [])
plt.show()
fig2, ax = plt.subplots(3, 1, dpi=200)
ax[0].plot(t, s2)
ax[1].plot(t, s4)
ax[2].plot(t, s2 + s4, 'r')
ax[0].set_title('sin( $\omega$t + $\pi$/2 )', loc='left')
ax[1].set_title('sin( 2*$\omega$t + $\pi/2$ )', loc='left')
ax[2].set_title('sin( $\omega$t + $\pi$/2 ) + sin( 2*$\omega$t + $\pi$/2 )', loc='left')
fix_axes()
for i in range(0, 3):
ax[i].set_xticks(np.arange(0, 3, 1), [])
plt.show()
fig3, ax = plt.subplots(3, 1, dpi=200)
ax[0].plot(t, s2)
ax[1].plot(t, s5)
ax[2].plot(t, s2 + s5, 'r')
ax[0].set_title('sin( $\omega$(t + $\pi$/2) )', loc='left')
ax[1].set_title('sin( 2*$\omega$t + 2*$\pi$/2 )', loc='left')
ax[2].set_title('sin( $\omega$t + $\pi$/2 ) + sin( 2*$\omega$t + 2*$\pi$/2 )', loc='left')
fix_axes()
for i in range(0, 3):
ax[i].set_xticks(np.arange(0, 3, 1), [])
plt.show()
|