Pracownia EEG/Potencjały wywołane: Różnice pomiędzy wersjami
AnnADuszyk (dyskusja | edycje) (Anulowanie wersji 10790 autorstwa AnnADuszyk (dyskusja)) Znacznik: Anulowanie edycji |
(Anulowanie wersji 10789 autorstwa AnnADuszyk (dyskusja)) Znacznik: Anulowanie edycji |
||
| (Nie pokazano 7 wersji utworzonych przez 2 użytkowników) | |||
| Linia 1: | Linia 1: | ||
| − | [[Pracownia EEG | + | [[Pracownia EEG|Pracownia EEG]] / Potencjały wywołane |
=Wstęp= | =Wstęp= | ||
| Linia 6: | Linia 6: | ||
Potencjały wywołane EEG (ang. ''evoked potentials'', EP) są śladami odpowiedzi mózgu na bodźce. W przypadku MEG poprawnie mówi się o polach wywołanych (ang. ''evoked fields'', EF). | Potencjały wywołane EEG (ang. ''evoked potentials'', EP) są śladami odpowiedzi mózgu na bodźce. W przypadku MEG poprawnie mówi się o polach wywołanych (ang. ''evoked fields'', EF). | ||
Zwykle reakcja ta jest mała (wyjątek stanowią [[Elektroencefalografia/Metody_analizy_sygnałów_EEG_-_analiza_w_dziedzinie_czasu |kompleksy K]]) i w zapisie pojedynczej realizacji reakcji na bodziec najczęściej niewidoczna wśród czynności pochodzącej od wielu innych procesów zachodzących w tym samym czasie w mózgu. | Zwykle reakcja ta jest mała (wyjątek stanowią [[Elektroencefalografia/Metody_analizy_sygnałów_EEG_-_analiza_w_dziedzinie_czasu |kompleksy K]]) i w zapisie pojedynczej realizacji reakcji na bodziec najczęściej niewidoczna wśród czynności pochodzącej od wielu innych procesów zachodzących w tym samym czasie w mózgu. | ||
| − | Ich wyodrębnienie z tak zwanego tła EEG/MEG, czyli manifestacji elektrycznej innych, trwających w tym samym czasie w mózgu procesów (aktywny prąd niezależny), wymaga w dniu dzisiejszym zapisu odpowiedzi na szereg powtórzeń tego samego bodźca (<xr id="fig:EP">rys. %i</xr>). Pierwsze potencjały wywołane pokazał pod koniec lat 40-tych Dawson (Dawson | + | Ich wyodrębnienie z tak zwanego tła EEG/MEG, czyli manifestacji elektrycznej innych, trwających w tym samym czasie w mózgu procesów (aktywny prąd niezależny), wymaga w dniu dzisiejszym zapisu odpowiedzi na szereg powtórzeń tego samego bodźca (<xr id="fig:EP">rys. %i</xr>). Pierwsze potencjały wywołane pokazał pod koniec lat 40-tych Dawson (Dawson 1947) wykonując superpozycję pojedynczych realizacji na kliszy fotograficznej. |
Z czasem skomplikowane urządzenia analogowe zastąpione zostały przez cyfrowe uśrednianie kolejnych fragmentów EEG, zsynchronizowanych według momentu wystąpienia bodźca, łatwo realizowane za pomocą komputera. | Z czasem skomplikowane urządzenia analogowe zastąpione zostały przez cyfrowe uśrednianie kolejnych fragmentów EEG, zsynchronizowanych według momentu wystąpienia bodźca, łatwo realizowane za pomocą komputera. | ||
| Linia 28: | Linia 28: | ||
Orientacyjny schemat załamków rozpoznawanych w słuchowych potencjach wywołanych, na podstawie (Szelenberger 2000). Skala czasu logarytmiczna. Najszybsze (do 12 ms) składowe egzogenne to potencjały pniowe (BAEP), oznaczane jako fale I-VII. Litery „P” i „N” oznaczają dodatnie i ujemne wychylenia związane z dalszymi załamkami]] | Orientacyjny schemat załamków rozpoznawanych w słuchowych potencjach wywołanych, na podstawie (Szelenberger 2000). Skala czasu logarytmiczna. Najszybsze (do 12 ms) składowe egzogenne to potencjały pniowe (BAEP), oznaczane jako fale I-VII. Litery „P” i „N” oznaczają dodatnie i ujemne wychylenia związane z dalszymi załamkami]] | ||
| − | Najszybsze (czyli o najmniejszej latencji) składowe to potencjały egzogenne, odzwierciedlające wstępne fazy | + | Najszybsze (czyli o najmniejszej latencji) składowe to potencjały egzogenne, odzwierciedlające wstępne fazy przekazu informacji. W potencjałach słuchowych są to potencjały pnia (ang. ''brainstem auditory evoked potentials'', BAEP), składające się z siedmiu fal występujących pomiędzy 1 a 12 ms od bodźca. Są one generowane np. w nerwie słuchowym czy pniu mózgu, i wykorzystywane w klinicznej diagnostyce integralności dróg słuchowych. Podobnie jak inne wczesne potencjały o latencjach poniżej 100 ms, są praktycznie niezależne od stanu uwagi. |
Po potencjałach o średniej latencji (między 12 a 50 ms) zaczynają się późne potencjały słuchowe (od 100 ms od podania bodźca), odzwierciedlające bardziej złożone reakcje na bodziec. Potencjały ok. 100 ms obserwowane w okolicach sensorycznych odzwierciedlają odpowiedź tejże kory na bodziec. Ich amplituda zależy od parametrów fizycznych bodźca oraz od uwagi, np. amplituda załamka N100 wzrasta w stanie skupienia uwagi czy pobudzenia emocjonalnego. Pierwszy i najpopularniejszy całkowicie endogenny załamek to P300, pojawiający się po rozpoznaniu bodźca oczekiwanego, na którym skupiamy uwagę: na przykład, jeśli w serii pojawiających się losowo liter mamy zliczać wystąpienia jednej z nich, to na średniej odpowiedzi na pojawienie się tej litery pojawi się załamek P300. Załamek ten występuje również w odpowiedzi na bodźce wyczekiwane, niespodziewane i ważne dla osoby (np. własne imię). | Po potencjałach o średniej latencji (między 12 a 50 ms) zaczynają się późne potencjały słuchowe (od 100 ms od podania bodźca), odzwierciedlające bardziej złożone reakcje na bodziec. Potencjały ok. 100 ms obserwowane w okolicach sensorycznych odzwierciedlają odpowiedź tejże kory na bodziec. Ich amplituda zależy od parametrów fizycznych bodźca oraz od uwagi, np. amplituda załamka N100 wzrasta w stanie skupienia uwagi czy pobudzenia emocjonalnego. Pierwszy i najpopularniejszy całkowicie endogenny załamek to P300, pojawiający się po rozpoznaniu bodźca oczekiwanego, na którym skupiamy uwagę: na przykład, jeśli w serii pojawiających się losowo liter mamy zliczać wystąpienia jednej z nich, to na średniej odpowiedzi na pojawienie się tej litery pojawi się załamek P300. Załamek ten występuje również w odpowiedzi na bodźce wyczekiwane, niespodziewane i ważne dla osoby (np. własne imię). | ||
| Linia 57: | Linia 57: | ||
====Wariancja w przypadku szumu skorelowanego ==== | ====Wariancja w przypadku szumu skorelowanego ==== | ||
| − | W poprzednim paragrafie pokazaliśmy, że w przypadku niezależnego szumu wariancja uśrednionego sygnału (w danej chwili czasu) maleje jak <math>\frac{1}{N}</math>. Jednak w przypadku gdy kolejne próbki szumu są skorelowane (np. występuje silna aktywność rytmiczna alfa) sytuacja się komplikuje. Intuicyjnie łatwo możemy to sobie wyobrazić w granicznym przypadku. Załóżmy, że tło dla potencjałów o stałej morfologii stanowi sinusoida. Jeśli będziemy podawać bodźce w odstępach będących wielokrotnością okresu tej sinusoidy to w uśrednianych fragmentach sygnału owa sinusoida jest tak samo powtarzalna jak badany potencjał i uśrednianie nie prowadzi do poprawy stosunku amplitudy sygnału do amplitudy tła. | + | W poprzednim paragrafie pokazaliśmy, że w przypadku niezależnego szumu wariancja uśrednionego sygnału (w danej chwili czasu) maleje jak <math>\frac{1}{N}</math>. Jednak w przypadku gdy kolejne próbki szumu są skorelowane (np. występuje silna aktywność rytmiczna alfa) sytuacja się komplikuje. Intuicyjnie łatwo możemy to sobie wyobrazić w granicznym przypadku. Załóżmy, że tło dla potencjałów o stałej morfologii stanowi sinusoida. Jeśli będziemy podawać bodźce w odstępach będących wielokrotnością okresu tej sinusoidy to w uśrednianych fragmentach sygnału owa sinusoida jest tak samo powtarzalna jak badany potencjał i uśrednianie nie prowadzi do poprawy stosunku amplitudy sygnału do amplitudy tła. |
Stopień zależności pomiędzy próbkami można zmierzyć przy pomocy funkcji autokorelacji. | Stopień zależności pomiędzy próbkami można zmierzyć przy pomocy funkcji autokorelacji. | ||
| Linia 75: | Linia 75: | ||
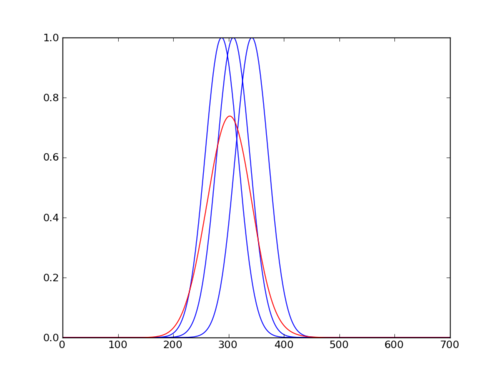
[[Grafika:Wariancja_latencji.png|thumb|500px|right| | [[Grafika:Wariancja_latencji.png|thumb|500px|right| | ||
Czerwona linia: Uśrednianie 100 potencjałów wywołanych o latncjach z rozkładu normalnego N(300,30 ), Niebieskie linie: przykładowe pojedyncze realizacje wzięte do średniej]]<!--# -*- coding: utf-8 -*- | Czerwona linia: Uśrednianie 100 potencjałów wywołanych o latncjach z rozkładu normalnego N(300,30 ), Niebieskie linie: przykładowe pojedyncze realizacje wzięte do średniej]]<!--# -*- coding: utf-8 -*- | ||
| − | + | from __future__ import division | |
| + | import numpy as np | ||
| + | from matplotlib.pyplot import plot, show ,subplot, figure, title, xlabel, ylabel, ylim | ||
| + | |||
| + | def fun(t,lat=100): | ||
| + | return np.exp(-(t-lat)**2/(2*30**2)) | ||
| + | Fs = 1 | ||
| + | N = 100 | ||
| + | t = np.arange(0,700) | ||
| + | f = np.zeros((N,700)) | ||
| + | f_sr = np.zeros(t.shape) | ||
| + | for i in range(N): | ||
| + | f[i,:] = fun(t,lat = 300 + 30* np.random.randn()) | ||
| + | for i in range(3): | ||
| + | plot(t,f[i,:], 'b') | ||
| + | plot(t,f.mean(0),'r') | ||
| + | show()--> | ||
Zmienność latencji prowadzi do: | Zmienność latencji prowadzi do: | ||
* zmniejszenia amplitudy <math>\bar x</math> | * zmniejszenia amplitudy <math>\bar x</math> | ||
| Linia 83: | Linia 99: | ||
Naturalne jest, że zmienność latencji jest bardziej widoczna w przypadku załamków trwających krótko niż w przypadku załamków trwających długo. Wariancja latencji rożnie wraz z jej wartością, stąd wśród późnych składowych potencjałów wywołanych nie obserwuje się komponentów krótkotrwałych. | Naturalne jest, że zmienność latencji jest bardziej widoczna w przypadku załamków trwających krótko niż w przypadku załamków trwających długo. Wariancja latencji rożnie wraz z jej wartością, stąd wśród późnych składowych potencjałów wywołanych nie obserwuje się komponentów krótkotrwałych. | ||
| + | <!--====Uśrednianie metodą Woody'ego ==== | ||
| + | Model potencjału ze zmienną latencją i sposób na jego efektywniejsze uśrednianie zaproponował Woody (1967). Model ten zakłada, że w każdej realizacji występuje komponent addytywny <math>s_i(t)\;</math>, który co do kształtu jest stały, a pomiędzy realizacjami różni się tylko latencją: | ||
| + | : <math> s_i(t) = s(t +\Delta t_i)\;</math> | ||
| + | Woody zaproponował aby <math>\Delta t_i\;</math> szacować na podstawie maksimum funkcji korelacji wzajemnej pomiędzy ''i''-tą realizacją a wzorcem. W pierwszym kroku wzorcem jest średni potencjał uzyskany przez proste uśrednienie realizacji. Następnie w sposób iteracyjny dokonuje się: | ||
| + | * poprawek w wyrównaniu poszczególnych realizacji, | ||
| + | * obliczenia nowego wzorca poprzez uśrednienie realizacji po korekcie wyrównania, | ||
| + | * obliczenia nowych poprawek do wyrównania realizacji.--> | ||
===Habituacja === | ===Habituacja === | ||
| Linia 111: | Linia 134: | ||
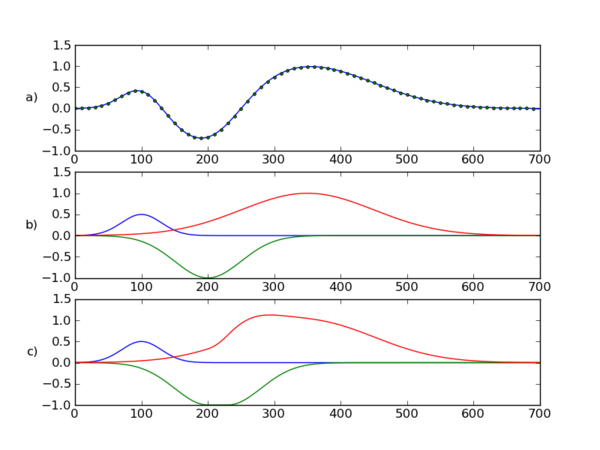
[[Plik:Sumowanie_komponentow1.png|center|thumb|600px| Panel a) przedstawia hipotetyczną krzywą ERP, panel b) jedna z możliwych dekompozycji sygnału w panelu a), panel c) inna możliwa dekompozycja sygnału z panelu a) ]] | [[Plik:Sumowanie_komponentow1.png|center|thumb|600px| Panel a) przedstawia hipotetyczną krzywą ERP, panel b) jedna z możliwych dekompozycji sygnału w panelu a), panel c) inna możliwa dekompozycja sygnału z panelu a) ]] | ||
| + | <source lang=python> | ||
| + | # -*- coding: utf-8 -*- | ||
| + | from __future__ import division | ||
| + | import numpy as np | ||
| + | from matplotlib.pyplot import plot, show ,subplot, figure, title, xlabel, ylabel, ylim | ||
| + | |||
| + | Fs = 1 | ||
| + | t = np.arange(0,700) | ||
| + | |||
| + | C1 = np.exp(-(t-100)**2/(2*30**2)) | ||
| + | C2 = np.exp(-(t-200)**2/(2*50**2)) | ||
| + | C3 = np.exp(-(t-350)**2/(2*100**2)) | ||
| + | ERP = 0.5*C1-C2+C3 | ||
| + | |||
| + | C2p = np.concatenate((C2[0:200], np.ones(30), C2[200:700-30] )) | ||
| + | C3p = ERP - 0.5*C1 + C2p | ||
| + | ERP_v2 = 0.5*C1-C2p+C3p | ||
| + | |||
| + | subplot(3,1,1) | ||
| + | plot(t,ERP, t[::10],ERP_v2[::10],'g.') | ||
| + | ylabel('a)',rotation='horizontal') | ||
| + | ylim([-1, 1.5]) | ||
| + | |||
| + | subplot(3,1,2) | ||
| + | plot(t,0.5*C1,t,-C2,t,C3) | ||
| + | ylabel('b)',rotation='horizontal') | ||
| + | ylim([-1, 1.5]) | ||
| + | |||
| + | subplot(3,1,3) | ||
| + | plot(t,0.5*C1,t,-C2p,t,C3p) | ||
| + | ylabel('c)',rotation='horizontal') | ||
| + | ylim([-1, 1.5]) | ||
| + | |||
| + | show() | ||
| + | </source> | ||
| + | |||
| + | ====Zmiana jednej komponenty może powodować zmiany w amplitudzie i latencji więcej niż jednego załamka.==== | ||
| + | Poniższy rysunek przedstawia sytuację gdy zmiana amplitudy jednego komponentu może znacząco wpływać na amplitudę i latencję innych załamków. | ||
| + | |||
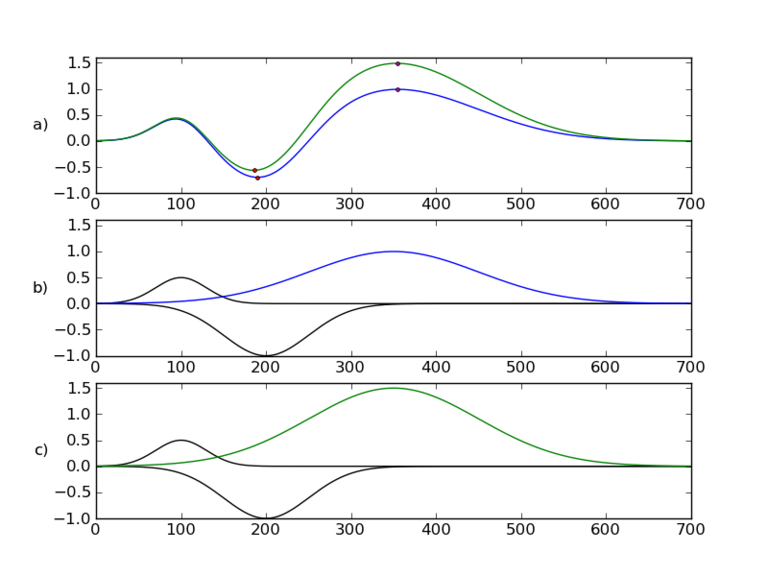
| + | [[Plik:Sumowanie_komponentow2.png|center|thumb|768px| Panel a) przedstawia dwie hipotetyczne krzywe ERP, panel b) panel b i c komponenty z których powstały owe krzywe. Zmiana amplitudy komponentu oznaczonego kolorem powoduje zmianę amplitudy oznaczonych załamków ale także zmianę latencji wcześniejszego załamka. ]] | ||
| + | Poniżej kod odtwarzający powyższy przykład: | ||
| + | <source lang = python> | ||
| + | # -*- coding: utf-8 -*- | ||
| + | from __future__ import division | ||
| + | import numpy as np | ||
| + | from matplotlib.pyplot import plot, show, subplot, figure, title, xlabel, ylabel, ylim | ||
| + | |||
| + | Fs = 1 | ||
| + | t = np.arange(0,700) | ||
| + | |||
| + | C1 = np.exp(-(t-100)**2/(2*30**2)) | ||
| + | C2 = np.exp(-(t-200)**2/(2*50**2)) | ||
| + | C3 = np.exp(-(t-350)**2/(2*100**2)) | ||
| + | ERP1 = 0.5*C1-C2+C3 | ||
| + | ERP2 = 0.5*C1-C2+1.5*C3 | ||
| + | |||
| + | |||
| + | subplot(3,1,1) | ||
| + | plot(t,ERP1,'b', t,ERP2,'g') | ||
| + | plot(t[np.argmin(ERP1)],np.min(ERP1),'r.' ) | ||
| + | plot(t[np.argmax(ERP1)],np.max(ERP1),'m.' ) | ||
| + | plot(t[np.argmin(ERP2)],np.min(ERP2),'r.' ) | ||
| + | plot(t[np.argmax(ERP2)],np.max(ERP2),'m.' ) | ||
| + | |||
| + | ylabel('a)',rotation='horizontal') | ||
| + | ylim([-1, 1.6]) | ||
| + | |||
| + | subplot(3,1,2) | ||
| + | plot(t,0.5*C1,'k',t,-C2,'k',t,C3,'b') | ||
| + | ylabel('b)',rotation='horizontal') | ||
| + | ylim([-1, 1.6]) | ||
| + | |||
| + | subplot(3,1,3) | ||
| + | plot(t,0.5*C1,'k',t,-C2,'k',t,1.5*C3,'g') | ||
| + | ylabel('c)',rotation='horizontal') | ||
| + | ylim([-1, 1.6]) | ||
| + | |||
| + | show() | ||
| + | </source> | ||
| + | |||
| + | =Instrukcje do ćwiczeń = | ||
| + | |||
| + | ==Zadanie 1: uśrednianie symulowanych sygnałów== | ||
| + | w tym ćwiczeniu chcemy pokazać efekty: | ||
| + | # uśredniania sygnałów związanych fazowo z bodźcem i nieskorelowanych z bodźcem / wpływ liczby realizacji, | ||
| + | # uśredniania sygnałów z fluktuacją latencji, | ||
| + | # wpływ filtrów o różnych funkcjach odpowiedzi impulsowej na morfologię uśrednionego potencjału. | ||
| + | |||
| + | ===Sygnały testowe=== | ||
| + | Proszę zaimplementować funkcje generujące następujące przebiegi czasowe (oznaczenia: ''F<sub>s</sub>'' — częstość próbkowania, ''T'' — czas trwania w sekundach, [[%C4%86wiczenia_1#Sygna.C5.82y_testowe|analogicznie do tego]]): | ||
| + | * sinusoida o zadanej częstości ''f'' i fazie <math>\phi</math>: <tt>y = sin(f, phi, Fs, T)</tt>, | ||
| + | * funkcja Gaussa o zadanym położeniu i szerokości <tt>y = g_1(t0, sigma, Fs, T) </tt> | ||
| + | : <math>g_1(t) = \exp\left(-\frac{(t-t_0)^2}{2 \sigma^2}\right)</math>, | ||
| + | * pochodną funkcji Gaussa o zadanym położeniu i szerokości <tt>y = g_2(t0, sigma, Fs, T)</tt>, | ||
| + | * połowę funkcji Gaussa o zadanym położeniu i szerokości <tt>y = g_3(t0, sigma, Fs, T)</tt>, | ||
| + | : <math>g_{3}(t) = \left\{ | ||
| + | \begin{array}{lll} | ||
| + | 0 & \mathrm{dla}& t<t_0 \\ | ||
| + | \exp\left(-\frac{(t-t_0)^2}{2 \sigma^2}\right)& \mathrm{dla}& t \ge t_0 | ||
| + | \end{array} | ||
| + | \right. </math>. | ||
| + | |||
| + | W dalszych zadaniach tej sekcji przyjmiemy: | ||
| + | * ''T'' = 1 s, | ||
| + | * ''F<sub>s</sub>'' = 128 Hz, | ||
| + | * ''t''<sub>0</sub> = 0,3 s, | ||
| + | * σ = 0,02 s. | ||
| + | |||
| + | ===Uśrednianie w modelu addytywnym: sygnał + szum=== | ||
| + | Dla funkcji <math>g_1</math>, <math>g_2</math> i <math>g_3</math> wykonaj ''N'' symulacji sygnału opisanego daną funkcją z dodanym szumem gaussowskim (<tt>numpy.random.randn</tt>). Zaobserwuj zmianę wariancji uśrednianego sygnału wraz z ''N''. | ||
| + | |||
| + | ===Uśrednianie w modelu addytywnym: sygnał + szum + niezależna czynność rytmiczna=== | ||
| + | Powtórz poprzednie symulacje dokładając w każdej realizacji sinusoidę o losowo wybranej fazie. Symulacje wykonaj dla różnych częstości sinusoidy, takich których połówka okresu zbliżona jest do szerokości funkcji Gaussa, oraz znacząco od niej różnych. | ||
| + | |||
| + | ===Uśrednianie w modelu z resetem fazy=== | ||
| + | Zbuduj sygnał składający się z dwóch fragmentów sinusoidy o częstości ''f'': | ||
| + | * pierwszy fragment ma losową fazę, | ||
| + | * drugi fragment ma fazę równą 0. | ||
| + | Wykonaj ''N'' realizacji takiego sygnału, przy czym każda realizacja ma częstość losowaną z rozkładu Gaussa o średniej 10 i pewnej wariancji (czyli <math>f \in \mathrm{N}(10,\sigma)</math>). | ||
| + | Uśrednij otrzymane realizacje. Zaobserwuj zależność średniej od liczby uśrednianych realizacji i od wariancji częstości. | ||
| + | |||
| + | ===Uśrednianie potencjału z fluktuacją latencji=== | ||
| + | Wygeneruj sygnały składające się z funkcji <math>g_1</math>, <math>g_2</math> albo <math>g_3</math> z fluktuującą latencją, tzn. z wartością <math>t_0</math> pochodzącą z jakiegoś rozkładu prawdopodobieństwa. U nas dla ustalenia uwagi niech będzie to rozkład Gaussa. Wykonaj zestaw symulacji obrazujący zależność od liczby realizacji i od wielkości fluktuacji, mierzonej przez wariancję rozkładu. Czy jest związek pomiędzy wariancją fluktuacji <math>t_0</math> a szerokością załamków? | ||
| + | |||
| + | ===Wpływ filtrów=== | ||
| + | # Zaprojektuj następujące filtry (przyjmij częstość próbkowania 128 Hz): | ||
| + | #* dolnoprzepustowy: Butterwortha z częstością odcięcia: 30, 40, 50 Hz, i rzędach od 1 do 5 (funkcja butter w module scipy.signal), | ||
| + | #* górnoprzepustowy: Butterwortha z częstością odcięcia: 0,1, 0,5, 2 i 5 Hz, i rzędach od 1 do 5, | ||
| + | #* notch: Czybyszewa II rodzaju z pasmem zaporowym ustawionym na 50 Hz, i rzędach od 1 do 3 (funkcja cheby2), | ||
| + | # Zbadaj funkcję odpowiedzi impulsowej i funkcję przenoszenia tych filtrów (w skali dB). Zaobserwuj jak długa jest odpowiedź impulsowa i jak daleko od częstości odcięcia zaburzone jest pasmo przenoszenia. | ||
| + | # Zastosuj powyższe filtry do funkcji <math>g_1</math>, <math>g_2</math> albo <math>g_3</math>. Filtrowanie przeprowadź w jedną (lfilter) oraz w dwie strony (filtfilt). Zaobserwuj związek między zniekształceniem wprowadzanym przez filtr a funkcją odpowiedzi impulsowej filtru. | ||
| + | # W ćwiczeniu tym posłuż się symulowanymi sygnałami uzyskanymi z modelu addytywnego: „sygnał+szum”. Dla funkcji <math>g_1</math>, <math>g_2</math> albo <math>g_3</math> wykonaj ''N'' = 60 realizacji sygnału opisanego daną funkcją z dodanym szumem gaussowskim (<tt>numpy.random.randn</tt>). Każdą z realizacji przefiltruj, a następnie uśrednij uzyskane sygnały. | ||
| + | |||
| + | ==Zadanie 2: rejestracje i analiza potencjałów wzrokowych== | ||
| + | |||
| + | <!-- ===Synchronizacja występowania bodźców z sygnałem EEG=== | ||
| + | |||
| + | Rejestracja potencjałów wywołanych jest przykładem pomiaru czynności elektrycznej mózgu w odpowiedzi na określony bodziec. W przypadku tego rodzaju pomiarów konieczna jest synchronizacja momentu wystąpienia bodźca z sygnałem EEG. Wzmacniacze do pomiaru czynności elektrycznej mózgu wyposażone są w specjalne wejścia, na które można podawać sygnał odpowiadający pojawianiu się bodźca. Jak pamiętamy z zeszłego semestru, wejście to (jak i podawany na nie sygnał) nazywamy trigerem (ang. ''trigger'' — spust, cyngiel, wyzwalacz). W najprostszym przypadku, bodziec moglibyśmy wyświetlać na monitorze komputerowym, a sygnał związany z jego wystąpieniem wysyłać przez któryś z portów komputera (LPT, COM) na wzmacniacz EEG. Niestety, obecnie dostępne i popularne systemy operacyjne, takie jak Windows czy Linux nie są systemami czasu rzeczywistego (http://pl.wikipedia.org/wiki/System_operacyjny_czasu_rzeczywistego). Od momentu wyświetlania bodźca na ekranie, do pojawiania się sygnału odpowiednim porcie komputerowym może upłynąć kilkadziesiąt milisekund i co gorsza czas ten zwykle jest losowy. W przypadku gdy wzmacniacz próbkuje sygnał z częstością 1000 Hz, moment wystąpienia bodźca możemy określić z dokładnością 1 ms, jednakże wspomniane opóźnienia w systemie operacyjnym uniemożliwiają to. Ponadto, jak dowiedzieliśmy się w rozdziale wstępnym [http://brain.fuw.edu.pl/edu-wiki/action/edit/EEG:Potencja%C5%82y_wywo%C5%82ane?section=T-1], pierwsze załamki związane z potencjałami wywołanymi pojawiają się już 10 ms po wystąpieniu bodźca. W związku z tym, losowe, rzędu kilkudziesięciu milisekund opóźnienia sygnału określającego moment pojawienia się bodźca względem jego rzeczywistego wystąpienia są niedopuszczalne. | ||
| + | Istnieją pewne techniki programowania, dzięki którym opisywane opóźnienia można zmniejszyć, jednakże są one bardzo trudne do realizacji. Ponadto, standardowe porty komputera, takie jak LPT, czy COM zostały zaprojektowane przede wszystkim do sterowania urządzeniami zewnętrznymi, a nie ich zasilania. Przykładowo, jedna linia portu drukarkowego (LPT) może być obciążona prądem nie większym niż 5 mA, podczas gdy do zapalenie zwykłej diody LED potrzeba około 10 mA. Taki pobór prądu możliwy jest do uzyskania z portu USB, jednakże jest on wyjątkowo trudny do oprogramowania. | ||
| + | W celu ominięcia powyższych niedogodności w Zakładzie Fizyki Biomedycznej UW w przeprowadzanych eksperymentach wykorzystywane są mikrokontrolery [http://pl.wikipedia.org/wiki/Mikrokontroler], w szczególności ATmega16 i ATmega32. Mikrokontrolery te wyposażone są w procesory o architekturze RISC [http://pl.wikipedia.org/wiki/RISC] i mocy obliczeniowej porównywalnej z szeroko stosowanym kiedyś w komputerach ZX Spectrum, Commodore, Amiga i Atari procesorem Z80. Oprócz jednostki centralnej mikrokontrolery zawierają stałą pamięć FLASH przeznaczoną do przechowywania kodu programu, pamięć RAM i pamięć EEPROM, liczniki 8- i 16-bitowe, komparatory, przetworniki analogowo-cyfrowe, porty wejścia/wyjścia, łącze RS232 (popularnie nazywane portem szeregowym) i układy przerwań. | ||
| + | |||
| + | Mikrokontrolery wchodzące w skład zestawów pomiarowych na Pracowni EEG zawierają program, który umożliwia komunikację z nimi poprzez port szeregowy. Obecnie, komputery są coraz rzadziej wyposażane w porty szeregowe. Standard komunikacji RS-232, opracowany w 1962 roku nadal jest jednak popularny i często wykorzystywany do komunikacji miedzy urządzeniami. W celu połączenia komputera posiadającego tylko porty USB z mikrokontrolerem zastosowano przejściówkę USB/RS-232. | ||
| + | |||
| + | Jak każde urządzenie w systemie Linuks, przejściówka USB/RS-232 widoczna jest jako plik, znajdujący się w katalogu <tt>/dev</tt>. Nazwy plików obsługujących urządzenia szeregowe to <tt>ttyXY</tt>, gdzie <tt>XY</tt> to kolejny numer przydzielony do urządzenia szeregowego. | ||
| + | Do komunikacji komputera z mikroknotrolerem w Zakładzie Fizyki Biomedycznej UW została napisana prosta biblioteka. Jej użycie jest następujące: | ||
| + | * Po podłączeniu przejściówki USB/RS232 do komputera mikrokontrolera sprawdź jaki plik w katalogu <tt>/dev</tt> został utworzony i przydzielony do urządzenia. | ||
| + | * Zaimportuj bibliotekę do komunikacji z mikrokontrolerem: | ||
| + | : <tt>import SerialPort as SP</tt> | ||
| + | |||
| + | * Otwórz plik powiązany z urządzeniem zewnętrznym: | ||
| + | : <tt>sp = SP.SerialPort(nazwa_pliku) </tt><br> | ||
| + | : <tt>sp.open()</tt> | ||
| + | W naszym przypadku prawidłowa nazwa pliku to <tt>/dev/ttyUSB0</tt>. | ||
| + | * Po włączeniu zasilania mikrokontrolera, diody podłączone do niego i wykorzystywane w eksperymencie z potencjałami wywołanymi będą zapalone. Następujące polecenie zgasi obydwie diody: | ||
| + | : <tt>sp.blinkP300([0, 0])</tt> | ||
| + | * Wydanie poniższego polecenia spowoduje, iż mikrokontroler zapali podłączoną do niego diodę numer 1 na czas 100 ms, zaś diodę numer 2 na 200 ms. Jednocześnie, w momencie włączenia jak i wyłączenia diody, sygnał z mikrokontrolera zostanie wysłany na 5-stykowe wejście AUX mikrokontrolera: | ||
| + | : <tt>sp.blinkP300([100, 200])</tt> | ||
| + | * Jeśli chcemy zapalić tylko diodę numer dwa, np. na czas 500 ms w programie podajemy następującą instrukcję: | ||
| + | : <tt>sp.blinkP300([0, 500])</tt> | ||
| + | * Jeśli chcemy zakończyć komunikację z mikrokontrolerem piszemy: | ||
| + | : <tt>sp.close()</tt> | ||
| + | |||
| + | Kod biblioteki do komunikacji z mikrokontrolerem:<br> | ||
| + | --><!-- Kod w Pythonie 2 | ||
| + | <source lang="python"> | ||
| + | # -*- coding: cp1250 -*- | ||
| + | import serial | ||
| + | import logging | ||
| + | import sys | ||
| + | import os | ||
| + | |||
| + | |||
| + | def to_hex_word(a): | ||
| + | '''encodes a decimal number hexadecimally on two bytes''' | ||
| + | return chr(a%256) + chr(a/256) | ||
| + | |||
| + | class SerialPort(object): | ||
| + | def __init__(self, port_name): | ||
| + | import serial | ||
| + | try: | ||
| + | self.port = serial.Serial( | ||
| + | port=port_name, | ||
| + | baudrate=9600, | ||
| + | bytesize=serial.EIGHTBITS, | ||
| + | parity=serial.PARITY_NONE, | ||
| + | stopbits=serial.STOPBITS_ONE, | ||
| + | xonxoff=False | ||
| + | ) | ||
| + | except serial.SerialException as e: | ||
| + | print("Nieprawidłowa nazwa portu lub port zajęty.") | ||
| + | raise e | ||
| + | self.close() | ||
| + | |||
| + | def open(self): | ||
| + | self.port.open() | ||
| + | |||
| + | def close(self): | ||
| + | self.port.close() | ||
| + | |||
| + | def send(self, value): | ||
| + | self.port.write(value) | ||
| + | |||
| + | def blinkSSVEP(self,d, p1, p2): | ||
| + | ''' | ||
| + | d = list of frequencies; | ||
| + | p1:p2 = ratio LED_on_time/LED_off_time | ||
| + | if you want i-th LED to be OFF all the time send d[i] = 0 | ||
| + | if you want i-th LED to be ON all the time send d[i] = -1 | ||
| + | in these two cases p1 and p2 do not matter | ||
| + | ''' | ||
| + | clock = 62500 | ||
| + | factor = float(p1) / float(p1 + p2) | ||
| + | |||
| + | str = chr(3) # 'SSVEP_RUN' | ||
| + | |||
| + | for i in range(len(d)): | ||
| + | # i-th LED OFF | ||
| + | if d[i] == 0: | ||
| + | str += to_hex_word(0) + to_hex_word(255) | ||
| + | # i-th LED ON | ||
| + | elif d[i] == -1: | ||
| + | str += to_hex_word(255) + to_hex_word(0) | ||
| + | #str = 'S' | ||
| + | # i-th LED blinks d[i] times per second | ||
| + | # p1:p2 = on_time:off_time in one blink | ||
| + | else: | ||
| + | period = clock/d[i] | ||
| + | bright = int((clock/d[i]) * factor) | ||
| + | dark = period - bright | ||
| + | str += to_hex_word(bright) + to_hex_word(dark) | ||
| + | |||
| + | self.send(str) | ||
| + | |||
| + | def blinkP300(self,d): | ||
| + | clock = 62500 | ||
| + | str = chr(4) # 'P300_RUN' | ||
| + | for i in range(len(d)): | ||
| + | period = int(clock*d[i]/1000.0) | ||
| + | str += to_hex_word(period) | ||
| + | print(period) | ||
| − | + | self.send(str) | |
| + | </source> | ||
| + | --><!-- Kod w Pythonie 3 --><!-- <source lang="python"> | ||
| + | # -*- coding: cp1250 -*- | ||
| + | import serial | ||
| + | import logging | ||
| + | import sys | ||
| + | import os | ||
| + | |||
| + | |||
| + | def to_hex_word(a): | ||
| + | '''encodes a decimal number hexadecimally on two bytes''' | ||
| + | return a.to_bytes(2,byteorder=sys.byteorder) | ||
| + | |||
| + | class SerialPort(object): | ||
| + | def __init__(self, port_name): | ||
| + | import serial | ||
| + | try: | ||
| + | self.port = serial.Serial( | ||
| + | port=port_name, | ||
| + | baudrate=9600, | ||
| + | bytesize=serial.EIGHTBITS, | ||
| + | parity=serial.PARITY_NONE, | ||
| + | stopbits=serial.STOPBITS_ONE, | ||
| + | xonxoff=False | ||
| + | ) | ||
| + | except serial.SerialException as e: | ||
| + | print("Nieprawidłowa nazwa portu lub port zajęty.") | ||
| + | raise e | ||
| + | self.close() | ||
| + | |||
| + | def open(self): | ||
| + | self.port.open() | ||
| + | |||
| + | def close(self): | ||
| + | self.port.close() | ||
| + | |||
| + | def send(self, value): | ||
| + | self.port.write(value) | ||
| + | |||
| + | def blinkSSVEP(self,d, p1, p2): | ||
| + | ''' | ||
| + | d = list of frequencies; | ||
| + | p1:p2 = ratio LED_on_time/LED_off_time | ||
| + | if you want i-th LED to be OFF all the time send d[i] = 0 | ||
| + | if you want i-th LED to be ON all the time send d[i] = -1 | ||
| + | in these two cases p1 and p2 do not matter | ||
| + | ''' | ||
| + | clock = 62500 | ||
| + | factor = float(p1) / float(p1 + p2) | ||
| + | |||
| + | str = (3).to_bytes(1,byteorder=sys.byteorder) # 'SSVEP_RUN' | ||
| + | |||
| + | for i in range(len(d)): | ||
| + | # i-th LED OFF | ||
| + | if d[i] == 0: | ||
| + | str += to_hex_word(0) + to_hex_word(255) | ||
| + | # i-th LED ON | ||
| + | elif d[i] == -1: | ||
| + | str += to_hex_word(255) + to_hex_word(0) | ||
| + | #str = 'S' | ||
| + | # i-th LED blinks d[i] times per second | ||
| + | # p1:p2 = on_time:off_time in one blink | ||
| + | else: | ||
| + | period = clock/d[i] | ||
| + | bright = int((clock/d[i]) * factor) | ||
| + | dark = int(period - bright) | ||
| + | str += to_hex_word(bright) + to_hex_word(dark) | ||
| + | |||
| + | self.send(str) | ||
| + | |||
| + | def blinkP300(self,d): | ||
| + | clock = 62500 | ||
| + | str = (4).to_bytes(1,byteorder=sys.byteorder) # 'P300_RUN' | ||
| + | |||
| + | for i in range(len(d)): | ||
| + | period = int(clock*d[i]/1000.0) | ||
| + | str += to_hex_word(period) | ||
| + | |||
| + | self.send(str) | ||
| + | </source> | ||
| + | --><!-- | ||
===Zestaw eksperymentalny=== | ===Zestaw eksperymentalny=== | ||
| Linia 147: | Linia 491: | ||
# Uśredniamy wycięte sygnały. | # Uśredniamy wycięte sygnały. | ||
# Rysujemy średni potencjał we wszystkich kanałach. | # Rysujemy średni potencjał we wszystkich kanałach. | ||
| − | # Pierwszy sposób analizy: Identyfikujemy załamki P1 i N2. Mierzymy amplitudę P1 jako różnicę między ekstremalną wartością załamka | + | # Pierwszy sposób analizy: Identyfikujemy załamki P1 i N2. Mierzymy amplitudę P1 jako różnicę między ekstremalną wartością załamka P1 a ekstremalną wartością załamka N2. |
# Drugi sposób analizy: Identyfikujemy załamki P1 i N2. Mierzymy amplitudę P1 w stosunku do zera. | # Drugi sposób analizy: Identyfikujemy załamki P1 i N2. Mierzymy amplitudę P1 w stosunku do zera. | ||
# Porównujemy uzyskane amplitudy w 4 warunkach za pomocą odpowiedniego testu statystycznego (porównanie warunków ze skrajnymi wartościami amplitudy) — zastosuj test permutacyjny (opisany poniżej) lub test t-Studenta/nieparametryczny odpowiednik). | # Porównujemy uzyskane amplitudy w 4 warunkach za pomocą odpowiedniego testu statystycznego (porównanie warunków ze skrajnymi wartościami amplitudy) — zastosuj test permutacyjny (opisany poniżej) lub test t-Studenta/nieparametryczny odpowiednik). | ||
Aktualna wersja na dzień 09:53, 8 paź 2024
Pracownia EEG / Potencjały wywołane
Spis treści
- 1 Wstęp
- 2 Instrukcje do ćwiczeń
Wstęp
Potencjały wywołane
Wstęp
Potencjały wywołane EEG (ang. evoked potentials, EP) są śladami odpowiedzi mózgu na bodźce. W przypadku MEG poprawnie mówi się o polach wywołanych (ang. evoked fields, EF). Zwykle reakcja ta jest mała (wyjątek stanowią kompleksy K) i w zapisie pojedynczej realizacji reakcji na bodziec najczęściej niewidoczna wśród czynności pochodzącej od wielu innych procesów zachodzących w tym samym czasie w mózgu. Ich wyodrębnienie z tak zwanego tła EEG/MEG, czyli manifestacji elektrycznej innych, trwających w tym samym czasie w mózgu procesów (aktywny prąd niezależny), wymaga w dniu dzisiejszym zapisu odpowiedzi na szereg powtórzeń tego samego bodźca (rys. 1). Pierwsze potencjały wywołane pokazał pod koniec lat 40-tych Dawson (Dawson 1947) wykonując superpozycję pojedynczych realizacji na kliszy fotograficznej. Z czasem skomplikowane urządzenia analogowe zastąpione zostały przez cyfrowe uśrednianie kolejnych fragmentów EEG, zsynchronizowanych według momentu wystąpienia bodźca, łatwo realizowane za pomocą komputera.
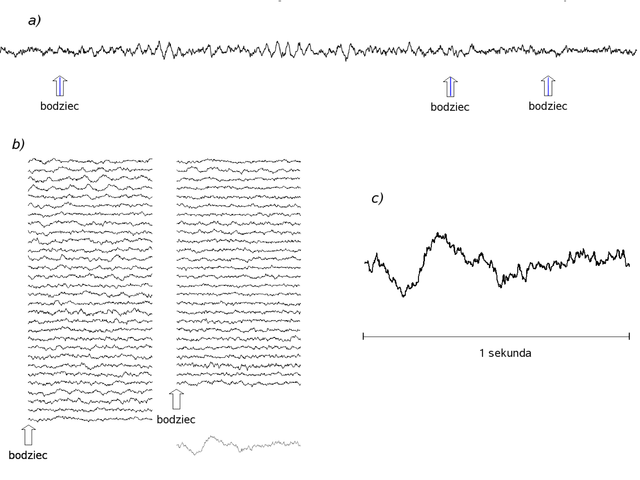
Techniki te opierają się na założeniu, że zawarta w EEG odpowiedź mózgu na każdy z kolejnych bodźców jest niezmienna, a EEG odzwierciedlające pozostałe procesy traktowane jest jak nieskorelowany z nią proces stochastyczny. Zależnie od rodzaju potencjałów wywołanych, założenia te są mniej lub bardziej nieuzasadnione; podważa je choćby powszechnie znany efekt habituacji, polegający na osłabieniu późnych potencjałów wywołanych kolejnymi powtórzeniami bodźca.
Istota potencjałów wywołanych jest przedmiotem otwartej dyskusji i dziesiątków prac, dotykających od lat podstawowych w tej dziedzinie pytań: czym jest potencjał wywołany, który widzimy w uśrednionym przebiegu? Czy naprawdę wynika z deterministycznie powtarzanej, jednakowej odpowiedzi pojawiającej się po każdym powtórzeniu bodźca niezależnie od „tła”, czy może wynika z reorganizacji faz tego właśnie „tła” EEG, czy może kombinacji tych dwóch efektów? Jest to wspaniałe pole dla zastosowań zaawansowanych metod modelowania i analizy sygnałów. W ostatnich latach powstają dziesiątki prac na ten temat, a od czasu do czasu również krytyczne artykuły wykazujące, że dotychczasowe odkrycia są raczej artefaktami stosowanych metod a nie wynikają z własności analizowanych danych (Yeung et al., 2004). Jak widać jest tu wciąż bardzo wiele do zrobienia, gdyż zrozumienie tego mechanizmu stoi na drodze do „świętego Graala”, którym w tej dziedzinie jest wyodrębnienie pojedynczych potencjałów wywołanych.
Niezależnie od tego, w neurofizjologii klinicznej nazwą potencjał wywołany określa się krzywą widoczną po uśrednieniu odpowiedzi na kilkanaście do kilku tysięcy bodźców (Szelenberger 2000). Gromadzona od dziesięcioleci wiedza o behawioralnych i klinicznych korelatach potencjałów wywołanych opiera się na rozpoznawaniu w przebiegach uśrednionych tak zwanych załamków, czyli przejściowych wzrostów lub spadków potencjału (na przykład na rys. 1 widać załamek P300). Nazwy załamków składają się zwykle z litery „P” (od ang. positive), jeśli wychylenie jest dodatnie, lub „N” (od ang. negative), jeśli wychylenie jest ujemne, oraz liczby. Uwaga:
- Nie ma niestety jednej ustalonej konwencji prezentacji potencjałów koniecznie trzeba więc zwracać uwagę na orientację wykresu, a wykonując wykres samemu - zamieszczać informację o orientacji kierunku dodatniego,gdyż kierunek dodatni może być wykresie skierowany do góry lub do dołu.
- Liczba następująca po N lub P określa przybliżoną liczbę milisekund od wystąpienia bodźca, czyli tak zwaną latencję. Nie można jednak ścisłego związku między tą liczbą a liczbą milisekund np. potencjał P300 w zależności od szczegółów paradygmatu doświadczalnego może wystąpić znacznie później. np. w eksperymentach językowych zdarza się że P300 występuje później niż N400 :-).
Rys. 2 przedstawia schematycznie najważniejsze załamki rozpoznawane w potencjałach słuchowych, czyli wywoływanych bodźcem dźwiękowym. Dla potencjałów wzrokowych i somatosensorycznych istnieją podobne klasyfikacje.
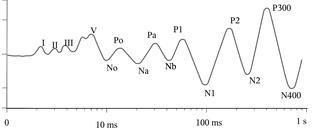
Najszybsze (czyli o najmniejszej latencji) składowe to potencjały egzogenne, odzwierciedlające wstępne fazy przekazu informacji. W potencjałach słuchowych są to potencjały pnia (ang. brainstem auditory evoked potentials, BAEP), składające się z siedmiu fal występujących pomiędzy 1 a 12 ms od bodźca. Są one generowane np. w nerwie słuchowym czy pniu mózgu, i wykorzystywane w klinicznej diagnostyce integralności dróg słuchowych. Podobnie jak inne wczesne potencjały o latencjach poniżej 100 ms, są praktycznie niezależne od stanu uwagi.
Po potencjałach o średniej latencji (między 12 a 50 ms) zaczynają się późne potencjały słuchowe (od 100 ms od podania bodźca), odzwierciedlające bardziej złożone reakcje na bodziec. Potencjały ok. 100 ms obserwowane w okolicach sensorycznych odzwierciedlają odpowiedź tejże kory na bodziec. Ich amplituda zależy od parametrów fizycznych bodźca oraz od uwagi, np. amplituda załamka N100 wzrasta w stanie skupienia uwagi czy pobudzenia emocjonalnego. Pierwszy i najpopularniejszy całkowicie endogenny załamek to P300, pojawiający się po rozpoznaniu bodźca oczekiwanego, na którym skupiamy uwagę: na przykład, jeśli w serii pojawiających się losowo liter mamy zliczać wystąpienia jednej z nich, to na średniej odpowiedzi na pojawienie się tej litery pojawi się załamek P300. Załamek ten występuje również w odpowiedzi na bodźce wyczekiwane, niespodziewane i ważne dla osoby (np. własne imię).
Uśrednianie w dziedzinie czasu
Jak już było wspomniane powyżej podstawową techniką stosowaną do analizy potencjałów wywołanych jest uśrednianie wielu realizacji odpowiedzi na bodziec wyrównanych względem jakiegoś charakterystycznego zdarzenia, np. momentu podania bodźca albo momentu behawioralnej reakcji na bodziec (np. wciśnięcie przycisku). Podejście to bazuje na trzech założeniach:
- Reakcja jest czasowo związana z bodźcem. Tzn. w kolejnych realizacjach występuje ona zawsze z tym samym opóźnieniem.
- Reakcja na bodziec skutkuje zawsze pojawieniem się w sygnale składowej o stałym kształcie (mówimy o stałej morfologii).
- Spontaniczna czynność EEG — ta która nie dotyczy przetwarzania interesującego nas bodźca — jest niezależnym, stacjonarnym szumem o średniej zero.
Zgodnie z powyższymi założeniami mierzony w i-tej realizacji sygnał można wyrazić jako:
- [math]x_i(t) = s(t) + n_i(t)[/math]
Uśrednianie po N realizacjach daje:
- [math]\bar x (t) = \frac{1}{N} \sum_{i=1}^N x_i(t) = \frac{1}{N} \left(N s(t) + \sum_{i=1}^N n_i(t) \right) [/math]
Wartość oczekiwana średniego sygnału wynosi:
- [math]\mathrm{E}\left[ \bar x(t) \right] = s(t) [/math]
gdyż dla szumu o średniej zero mamy:
- [math]\mathrm{E}\left[\frac{1}{N} \sum_{i=1}^N n_i(t)\right] = 0[/math].
Wariancja [math]\bar x(t)[/math] wynosi:
- [math]\sigma^2_{\bar x(t)} = \mathrm{E} \left[ \left( \frac{1}{N} \sum_{i=1}^N n_i(t)\right)^2 \right] \approx \frac{1}{N} \sigma^2_{n(t)}[/math]
gdyż [math]s(t)[/math] jest deterministyczne.
Dla potencjałów pojawiających się w pierwszych kilkudziesięciu milisekundach po bodźcu model ten można uznać za poprawny, gdyż wykazują one zależność głównie od parametrów fizycznych bodźca. Dla późniejszych składowych staje się on coraz bardziej wątpliwy ze względu na występujące korelacje ze stanem (np. uwagi) badanego.
Dla późniejszych składowych można by postulować bardziej ogólną wersję modelu potencjału wywołanego:
- [math]x_i(t) = s_i(t) + n_i(t)[/math]
Ten model uwidacznia, że do opisu potencjału wywołanego potrzebna jest nie tylko średnia, ale i wyższe momenty rozkładu (np. drugi moment centralny czyli wariancja).
Wariancja w przypadku szumu skorelowanego
W poprzednim paragrafie pokazaliśmy, że w przypadku niezależnego szumu wariancja uśrednionego sygnału (w danej chwili czasu) maleje jak [math]\frac{1}{N}[/math]. Jednak w przypadku gdy kolejne próbki szumu są skorelowane (np. występuje silna aktywność rytmiczna alfa) sytuacja się komplikuje. Intuicyjnie łatwo możemy to sobie wyobrazić w granicznym przypadku. Załóżmy, że tło dla potencjałów o stałej morfologii stanowi sinusoida. Jeśli będziemy podawać bodźce w odstępach będących wielokrotnością okresu tej sinusoidy to w uśrednianych fragmentach sygnału owa sinusoida jest tak samo powtarzalna jak badany potencjał i uśrednianie nie prowadzi do poprawy stosunku amplitudy sygnału do amplitudy tła.
Stopień zależności pomiędzy próbkami można zmierzyć przy pomocy funkcji autokorelacji. Jeśli funkcję autokorelacji przybliżymy przez:
- [math]R_{xx}(\tau) = \sigma^2 \exp(-\beta |\tau|) \cos(2 \pi f_0 \tau)[/math]
gdzie [math]\sigma^2[/math] jest wariancją szumu, [math]f_0[/math] jest średnią częstością aktywności rytmicznej, [math]\beta/ \pi[/math] jest szerokością pasma tej czynności, zaś [math]\tau[/math] opóźnieniem, to wariancję potencjału wywołanego można wyrazić jako:
- [math]\sigma^2_{\bar x(t)} = \frac{\sigma^2}{N} \left[ \frac{1-\exp(-2 \beta T)}{1 - 2 \exp(- \beta T) \cos(2 \pi f_0 T) +\exp(-2 \beta T)} \right] [/math]
gdzie [math]T[/math] jest odstępem między bodźcami. Widać stąd, że obecność czynności rytmicznej w tle wpływa na stosunek sygnału do szumu. Z powyższego równania widać, że stosunek wariancji dąży do [math]\frac{\sigma^2}{N}[/math] gdy [math]\beta T[/math] staje się duże.
Periodyczna stymulacja może ponadto prowadzić do wzbudzenia czynności rytmicznej o częstości równej częstości pobudzania bądź jej harmonicznej.
Wariancja latencji
Jedną z form zmienności potencjału wywołanego w pojedynczych realizacjach jest wariancja latencji.
Zmienność latencji prowadzi do:
- zmniejszenia amplitudy [math]\bar x[/math]
- wzrostu rozciągłości czasowej załamka
O tych konsekwencjach zmienności latencji należy w szczególności pamiętać porównując średnie potencjały uzyskane w różnych warunkach eksperymentalnych. Gdy zauważymy, że średnie potencjały różnią się amplitudą należy rozważyć możliwość, że w istocie warunki eksperymentalne wpływają na różnice w wariancji latencji.
Naturalne jest, że zmienność latencji jest bardziej widoczna w przypadku załamków trwających krótko niż w przypadku załamków trwających długo. Wariancja latencji rożnie wraz z jej wartością, stąd wśród późnych składowych potencjałów wywołanych nie obserwuje się komponentów krótkotrwałych.
Habituacja
Zmienność w odpowiedziach na kolejno występujące po sobie bodźce można podzielić na komponent stochastyczny i deterministyczny. Komponent deterministyczny odzwierciedla zmianę czułości układu nerwowego na kolejne bodźce. Nowy bodziec często wywołuje reakcje pobudzenia widoczną w wielu parametrach takich jak przewodnictwo skóry, rytm serca i reaktywność kory mózgowej. Powszechnie obserwowanym zjawiskiem jest spadek reaktywności na powtarzające się bodźce zwany habituacją. Niekiedy obserwuje się także zjawisko przeciwne — wzrost reaktywności na bodziec — zwane sensytyzacją.
Klasycznym sposobem na badanie tych zjawisk w potencjałach wywołanych jest uśrednianie w podzbiorach lub uśrednianie blokowe. Wymaga ono zmiany paradygmatu rejestracji danych. Załóżmy, że interesującym nas bodźcem jest błysk światła. Chcemy zaobserwować ewentualne zmiany amplitudy i latencji w ciągu 100 potencjałów będących reakcją na błysk powtarzający się co 500 ms.
Uśrednianie w podzbiorach
W metodzie tej musimy założyć, że proces habituacji jest powolny, tzn. zmiany pomiędzy kolejnymi reakcjami są bardzo małe. W takim przypadku możemy podzielić długą serię bodźców na ciąg pod-serii i uśrednienie przeprowadzić dla każdej pod-serii osobno.
Uśrednianie blokowe
W tym celu eksperyment wykonujemy w wielu seriach. Jedna seria składa się ze 100 błysków powtarzanych co 500 ms. Po serii następuje przerwa trwająca np. 5 s (długość przerwy wyraża nasze oszacowanie czasu potrzebnego na zanik habituacji). Po przerwie seria jest powtarzana. Powtórzeń serii wykonujemy N. Następnie uśredniamy fragmenty sygnałów odpowiadające sobie w kolejnych seriach.
W tym paradygmacie zakładamy, że każda seria rejestrowana jest w tych samych warunkach. Zaniedbujemy efekty związane ze zmęczeniem i zmianami w np. stopniu koncentracji badanego.
Załamki w krzywej potencjału wywołanego vs ukryte komponenty
Komponenta potencjału wywołanego to bardzo ważne ale jednocześnie źle określone pojęcie. Krzywa otrzymana w wyniku uśredniania potencjałów wywołanych przedstawia serię załamków dodatnich i ujemnych, ale trzeba być świadomym, że ten przebieg napięcia rejestrowany przez elektrody przedstawia tak naprawdę sumę potencjałów pochodzących od wielu dość niezależnie działających źródeł w mózgu. Przyczynek pochodzący od jednego funkcjonalnego źródła będziemy określać jako komponentę.
Komentarza wymaga też pojęcie źródła funkcjonalnego. Czynność elektryczną synchronicznie działających neuronów piramidalnych w określonym fragmencie kory mózgowej z pewnej odległości można przybliżyć potencjałem dipola prądowego. Taki aktywny fragment kory stanowi źródło dające przyczynek do mierzonego na powierzchni głowy potencjału. W najprostszej sytuacji taki przyczynek może być obserwowany jako komponenta. Mózg jest jednak obiektem niezwykle złożonym i gęsto połączonym. Wiele obszarów korowych może być funkcjonalnie połączonych i aktywowanych synchronicznie w celu realizacji określonego zadania — o takim funkcjonalnym zespole też możemy myśleć jako o pojedynczym źródle, choć może ono mieć złożoną strukturę przestrzenną. Często zatem myślimy o komponentach ukrytych potencjału wywołanego jako o aktywności takich funkcjonalnych zespołów.
Po tym wstępie widać już chyba, że do zrozumienia co dzieje się w czasie reakcji na bodziec, którą obserwujemy w potencjale wywołanym, bardziej pożądane byłoby badanie komponent ukrytych niż poszczególnych załamków krzywej potencjału wywołanego, która stanowi ważoną sumę owych komponentów. Zanim przejdziemy do omówienia technik służących „wyłuskiwaniu” komponent prześledźmy kilka symulacji i wnioski z nich płynące.
Załamki i komponenty nie są tym samym.
Tę samą krzywą można otrzymać na nieskończenie wiele sposobów przez sumowanie rożnych kombinacji domniemanych komponentów. Przykładowy rysunek pokazuje, jak tę samą krzywą można złożyć z dwóch rożnych zestawów komponentów (kod wytwarzający przykładową symulację pokazany jest poniżej).
# -*- coding: utf-8 -*-
from __future__ import division
import numpy as np
from matplotlib.pyplot import plot, show ,subplot, figure, title, xlabel, ylabel, ylim
Fs = 1
t = np.arange(0,700)
C1 = np.exp(-(t-100)**2/(2*30**2))
C2 = np.exp(-(t-200)**2/(2*50**2))
C3 = np.exp(-(t-350)**2/(2*100**2))
ERP = 0.5*C1-C2+C3
C2p = np.concatenate((C2[0:200], np.ones(30), C2[200:700-30] ))
C3p = ERP - 0.5*C1 + C2p
ERP_v2 = 0.5*C1-C2p+C3p
subplot(3,1,1)
plot(t,ERP, t[::10],ERP_v2[::10],'g.')
ylabel('a)',rotation='horizontal')
ylim([-1, 1.5])
subplot(3,1,2)
plot(t,0.5*C1,t,-C2,t,C3)
ylabel('b)',rotation='horizontal')
ylim([-1, 1.5])
subplot(3,1,3)
plot(t,0.5*C1,t,-C2p,t,C3p)
ylabel('c)',rotation='horizontal')
ylim([-1, 1.5])
show()
Zmiana jednej komponenty może powodować zmiany w amplitudzie i latencji więcej niż jednego załamka.
Poniższy rysunek przedstawia sytuację gdy zmiana amplitudy jednego komponentu może znacząco wpływać na amplitudę i latencję innych załamków.
Poniżej kod odtwarzający powyższy przykład:
# -*- coding: utf-8 -*-
from __future__ import division
import numpy as np
from matplotlib.pyplot import plot, show, subplot, figure, title, xlabel, ylabel, ylim
Fs = 1
t = np.arange(0,700)
C1 = np.exp(-(t-100)**2/(2*30**2))
C2 = np.exp(-(t-200)**2/(2*50**2))
C3 = np.exp(-(t-350)**2/(2*100**2))
ERP1 = 0.5*C1-C2+C3
ERP2 = 0.5*C1-C2+1.5*C3
subplot(3,1,1)
plot(t,ERP1,'b', t,ERP2,'g')
plot(t[np.argmin(ERP1)],np.min(ERP1),'r.' )
plot(t[np.argmax(ERP1)],np.max(ERP1),'m.' )
plot(t[np.argmin(ERP2)],np.min(ERP2),'r.' )
plot(t[np.argmax(ERP2)],np.max(ERP2),'m.' )
ylabel('a)',rotation='horizontal')
ylim([-1, 1.6])
subplot(3,1,2)
plot(t,0.5*C1,'k',t,-C2,'k',t,C3,'b')
ylabel('b)',rotation='horizontal')
ylim([-1, 1.6])
subplot(3,1,3)
plot(t,0.5*C1,'k',t,-C2,'k',t,1.5*C3,'g')
ylabel('c)',rotation='horizontal')
ylim([-1, 1.6])
show()
Instrukcje do ćwiczeń
Zadanie 1: uśrednianie symulowanych sygnałów
w tym ćwiczeniu chcemy pokazać efekty:
- uśredniania sygnałów związanych fazowo z bodźcem i nieskorelowanych z bodźcem / wpływ liczby realizacji,
- uśredniania sygnałów z fluktuacją latencji,
- wpływ filtrów o różnych funkcjach odpowiedzi impulsowej na morfologię uśrednionego potencjału.
Sygnały testowe
Proszę zaimplementować funkcje generujące następujące przebiegi czasowe (oznaczenia: Fs — częstość próbkowania, T — czas trwania w sekundach, analogicznie do tego):
- sinusoida o zadanej częstości f i fazie [math]\phi[/math]: y = sin(f, phi, Fs, T),
- funkcja Gaussa o zadanym położeniu i szerokości y = g_1(t0, sigma, Fs, T)
- [math]g_1(t) = \exp\left(-\frac{(t-t_0)^2}{2 \sigma^2}\right)[/math],
- pochodną funkcji Gaussa o zadanym położeniu i szerokości y = g_2(t0, sigma, Fs, T),
- połowę funkcji Gaussa o zadanym położeniu i szerokości y = g_3(t0, sigma, Fs, T),
- [math]g_{3}(t) = \left\{ \begin{array}{lll} 0 & \mathrm{dla}& t\lt t_0 \\ \exp\left(-\frac{(t-t_0)^2}{2 \sigma^2}\right)& \mathrm{dla}& t \ge t_0 \end{array} \right. [/math].
W dalszych zadaniach tej sekcji przyjmiemy:
- T = 1 s,
- Fs = 128 Hz,
- t0 = 0,3 s,
- σ = 0,02 s.
Uśrednianie w modelu addytywnym: sygnał + szum
Dla funkcji [math]g_1[/math], [math]g_2[/math] i [math]g_3[/math] wykonaj N symulacji sygnału opisanego daną funkcją z dodanym szumem gaussowskim (numpy.random.randn). Zaobserwuj zmianę wariancji uśrednianego sygnału wraz z N.
Uśrednianie w modelu addytywnym: sygnał + szum + niezależna czynność rytmiczna
Powtórz poprzednie symulacje dokładając w każdej realizacji sinusoidę o losowo wybranej fazie. Symulacje wykonaj dla różnych częstości sinusoidy, takich których połówka okresu zbliżona jest do szerokości funkcji Gaussa, oraz znacząco od niej różnych.
Uśrednianie w modelu z resetem fazy
Zbuduj sygnał składający się z dwóch fragmentów sinusoidy o częstości f:
- pierwszy fragment ma losową fazę,
- drugi fragment ma fazę równą 0.
Wykonaj N realizacji takiego sygnału, przy czym każda realizacja ma częstość losowaną z rozkładu Gaussa o średniej 10 i pewnej wariancji (czyli [math]f \in \mathrm{N}(10,\sigma)[/math]). Uśrednij otrzymane realizacje. Zaobserwuj zależność średniej od liczby uśrednianych realizacji i od wariancji częstości.
Uśrednianie potencjału z fluktuacją latencji
Wygeneruj sygnały składające się z funkcji [math]g_1[/math], [math]g_2[/math] albo [math]g_3[/math] z fluktuującą latencją, tzn. z wartością [math]t_0[/math] pochodzącą z jakiegoś rozkładu prawdopodobieństwa. U nas dla ustalenia uwagi niech będzie to rozkład Gaussa. Wykonaj zestaw symulacji obrazujący zależność od liczby realizacji i od wielkości fluktuacji, mierzonej przez wariancję rozkładu. Czy jest związek pomiędzy wariancją fluktuacji [math]t_0[/math] a szerokością załamków?
Wpływ filtrów
- Zaprojektuj następujące filtry (przyjmij częstość próbkowania 128 Hz):
- dolnoprzepustowy: Butterwortha z częstością odcięcia: 30, 40, 50 Hz, i rzędach od 1 do 5 (funkcja butter w module scipy.signal),
- górnoprzepustowy: Butterwortha z częstością odcięcia: 0,1, 0,5, 2 i 5 Hz, i rzędach od 1 do 5,
- notch: Czybyszewa II rodzaju z pasmem zaporowym ustawionym na 50 Hz, i rzędach od 1 do 3 (funkcja cheby2),
- Zbadaj funkcję odpowiedzi impulsowej i funkcję przenoszenia tych filtrów (w skali dB). Zaobserwuj jak długa jest odpowiedź impulsowa i jak daleko od częstości odcięcia zaburzone jest pasmo przenoszenia.
- Zastosuj powyższe filtry do funkcji [math]g_1[/math], [math]g_2[/math] albo [math]g_3[/math]. Filtrowanie przeprowadź w jedną (lfilter) oraz w dwie strony (filtfilt). Zaobserwuj związek między zniekształceniem wprowadzanym przez filtr a funkcją odpowiedzi impulsowej filtru.
- W ćwiczeniu tym posłuż się symulowanymi sygnałami uzyskanymi z modelu addytywnego: „sygnał+szum”. Dla funkcji [math]g_1[/math], [math]g_2[/math] albo [math]g_3[/math] wykonaj N = 60 realizacji sygnału opisanego daną funkcją z dodanym szumem gaussowskim (numpy.random.randn). Każdą z realizacji przefiltruj, a następnie uśrednij uzyskane sygnały.
Zadanie 2: rejestracje i analiza potencjałów wzrokowych
Eksperyment 1. Obserwacja bodźca wzrokowego
Proszę zapoznać się z typowym wyglądem załamków w przypadku potencjałów wzrokowych, jaki jest przedstawiony na rysunku (cały artykuł jest dostępny tu).
Rejestracja
- Paradygmat: z odległości około 40 cm badany obserwuje wyświetalny na ekranie biały kwadrat. Bodźce trwają 300 ms i powtarzają się co 0,5 sekundy. Bodziec poprzedza punkt fiksacji pokazywany przez 300 ms. Natężenie bodźca ma przyjąć jedną z 4 wartości (manipulujemy jego przeźroczystością: 1, 0,7, 0,3 i 0,1, gdzie 1 oznacza brak przeźroczystości). Każda z intensywności bodźca ma pojawić się 100 razy podczas badania, bodźce podawane mają być w sposób losowy. Zadanie poprzedza krótka instrukcja, a kończy podziękowanie.
- Pomiar
- Zakładamy czepek i elektrody w systemie 10-20, dbamy o to by opory pomiędzy elektrodami były poniżej 10 kΩ i różnice pomiędzy oporami różnych elektrod nie przekraczały 20%.
- Elektrodę GND mocujemy w otworze czepka odpowiadającym pozycji AFz (na linii centralnej 10% w stronę nosa od elektrody Fz)
- Montujemy także elektrody M1 i M2 i FCz.
Analiza
- W sygnale wyszukujemy wzrokowo odcinki z artefaktami i oznaczamy je tagami w SVAROGu.
- Filtrujemy sygnał w paśmie 1-20 Hz.
- Z ciągłego zapisu wycinamy fragmenty od −300 ms do +800 ms (zero oznacza moment wystąpienia bodźca). W czasie wycinania badamy wycinane fragmenty pod względem zakresu amplitudy (wszystkie kanały powinny mieć amplitudę w granicach ±75 μV) i zawartości artefaktów od mrugania (w tym celu trzeba oglądając sygnał w SVAROG-u ustalić próg na amplitudę sygnału w kanałach Fp1 i Fp2).
- W przypadku, gdy dane są zanieczyszczone wieloma mrugnięciami (zwłaszcza tylnych okolicach), należy skorzystać z metody ICA w SVAROGU, informacje tutaj: [1])
- Porównujemy zestawy danych otrzymane po wzrokowym i automatycznym (metodą opisaną powyżej) usunięciu artefaktów.
- Uśredniamy wycięte sygnały.
- Rysujemy średni potencjał we wszystkich kanałach.
- Pierwszy sposób analizy: Identyfikujemy załamki P1 i N2. Mierzymy amplitudę P1 jako różnicę między ekstremalną wartością załamka P1 a ekstremalną wartością załamka N2.
- Drugi sposób analizy: Identyfikujemy załamki P1 i N2. Mierzymy amplitudę P1 w stosunku do zera.
- Porównujemy uzyskane amplitudy w 4 warunkach za pomocą odpowiedniego testu statystycznego (porównanie warunków ze skrajnymi wartościami amplitudy) — zastosuj test permutacyjny (opisany poniżej) lub test t-Studenta/nieparametryczny odpowiednik).
- Opis testu permutacyjnego
Pytanie: Czy intensywność bodźca wpływa na amplitudę potencjału P1? Jak stwierdzić czy amplitudy załamków P1 istotnie różnią się pomiędzy seriami?
Musimy przeprowadzić test statystyczny. Możemy skonstruować go np. tak: Mamy dwa warunki I i II. Jako statystykę przyjmiemy różnicę pomiędzy amplitudą załamka zmierzoną w serii z dwoma diodami (P2II) a amplitudą zmierzoną w serii z jedną diodą (P2I):
- S = P2II − P2I
Postawmy hipotezę zerową, że nie ma różnicy w amplitudzie pomiędzy warunkiem II a I oraz hipotezę alternatywną, że różnica taka występuje.
- H0: S = 0
- H1: S ≠ 0
Zgodnie z H0 dla wartości S nie ma różnicy czy realizacja została zarejestrowana w warunkach I czy II, zatem można losowo poprzypisywać numery warunków do realizacji i w ten sposób uzyskać rozkład statystyki S pod warunkiem prawdziwości H0, czyli obliczyć średnie potencjały dla „pomieszanych” tagów, wyliczyć średnie potencjały dla sztucznie wygenerowaych grup, i wyliczyć różnicę amplitud dla tych średnich, czyli wartość statystyki dla hipotezy H0.
Zaimplementuj test permutacyjny zgodny z powyższą koncepcją.
Eksperyment 2: rejestracja i analiza potencjału P3
Rejestracja
- Paradygmat:
- z odległości około 40 cm badany obserwuje kwadrat, który występuje w dwóch kolorach.
- Bodźce trwają 300 ms, poprzedzane punktem fiksacji wyświetlanym na 300 ms, przerwa między próbami jest losowana i wynosi od 0.8-1.2 s.
- Proporcja wystapień bodźców koloru pierwszego i drugiego wynosi 1:5.
- Zadaniem badanego jest liczenie kwadratów w rzadkim kolorze.
- Wykonujemy tyle realizacji aby zarejestrować 100 powtórzeń bodźców rzadkich.
- Zakładamy czepek i elektrody w systemie 10-20, dbamy o to by opory pomiędzy elektrodami były poniżej 5 kΩ i różnice pomiędzy oporami różnych elektrod nie przekraczały 20%.
- Elektrodę GND mocujemy w otworze czepka odpowiadającym pozycji AFz (na linii centralnej 10% w stronę nosa od elektrody Fz)
- Montujemy także elektrody M1 i M2, będziemy ich używać w montażu i w czasie analizy jako referencji typu połączone uszy.
- Częstość próbkowania 512 Hz.
Analiza
- Filtrujemy sygnał w paśmie 1-20 Hz.
- Z ciągłego zapisu wycinamy fragmenty od −300 ms do +900 ms (zero oznacza moment wystąpienia bodźca). W czasie wycinania badamy wycinane fragmenty pod względem zakresu amplitudy (wszystkie kanały powinny mieć amplitudę w granicach ±75 μV) i zawartości artefaktów od mrugania (w tym celu trzeba oglądając sygnał w SVAROG-u ustalić próg na amplitudę sygnału w kanałach Fp1 i Fp2).
- Uśredniamy osobno realizacje dla każdego koloru kwadratu.
- Nakładamy na siebie na rysunkach oba typy średnich.
- Wyznaczamy amplitudę P3 i liczymy test statystyczny pomiędzy warunkami.
Zadanie 3. Analiza Heartbeat-Evoked Potential (HEP)
Celem tego zadania jest zaobserwowanie występowania ERP związanego z działaniem serca (szczegóły można doczytać tutaj: [2]. W zadaniu tym wykorzystany dane spoczynkowe zebrane podczas pierwszej rejestracji.
- w pierwszym kroku sygnał montujemy i filtrujemy;
- następnie zaznaczamy fragmenty sygnału, w których widzimy artefakty;
- w drugim robimy detekcję załamków R z EKG — po ich podstawie będziemy cieli sygnał (−200-600 ms po R);
- następnie uśredniamy otrzymane odcinki.