Elektrodynamika/Seria 4: Różnice pomiędzy wersjami
SuperAdmin (dyskusja | edycje) (Utworzono nową stronę "<div align="center"> <b>Elektrodynamika dla Neuroinformatyki</b> <b>Seria 4</b> </div> ==Zadanie 1== Znaleźć rozkład natężenia <math> \vec{E}</math> oraz pote...") |
|||
| Linia 11: | Linia 11: | ||
Znaleźć rozkład natężenia <math> \vec{E}</math> oraz potencjału <math> V </math> pola elektrycznego, pochodzącego od punktowego ładunku elektrycznego <math> Q </math> umieszczonego w odległości <math> d </math> od powierzchni nieskończonej uziemionej płaszczyzny przewodzącej. Jaki ładunek jest indukowany na powierzchni tej płaszczyzny? | Znaleźć rozkład natężenia <math> \vec{E}</math> oraz potencjału <math> V </math> pola elektrycznego, pochodzącego od punktowego ładunku elektrycznego <math> Q </math> umieszczonego w odległości <math> d </math> od powierzchni nieskończonej uziemionej płaszczyzny przewodzącej. Jaki ładunek jest indukowany na powierzchni tej płaszczyzny? | ||
| − | |||
| − | |||
==Zadanie 2== | ==Zadanie 2== | ||
Aktualna wersja na dzień 08:01, 21 maj 2015
Elektrodynamika dla Neuroinformatyki
Seria 4
Spis treści
Zadanie 1
Znaleźć rozkład natężenia [math] \vec{E}[/math] oraz potencjału [math] V [/math] pola elektrycznego, pochodzącego od punktowego ładunku elektrycznego [math] Q [/math] umieszczonego w odległości [math] d [/math] od powierzchni nieskończonej uziemionej płaszczyzny przewodzącej. Jaki ładunek jest indukowany na powierzchni tej płaszczyzny?
Zadanie 2
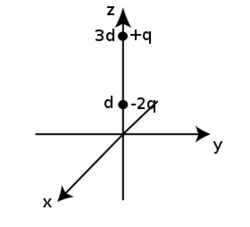
Znaleźć siłę działającą na ładunek [math]+q[/math] w układzie przedstawionym na poniższym rysunku. Płaszczyzna [math]xy[/math] jest powierzchnią nieskończonego, uziemionego przewodnika.
Zadanie 3
Ładunek punktowy [math]q[/math] umieszczono w odległości [math]a[/math] od wykonanej z przewodnika, uziemionej kuli o promieniu [math]R[/math]. Znaleźć potencjał elektryczny na zewnątrz kuli. W jaki sposób należałoby rozwiązać podobne zadanie, w którym na kuli byłby utrzymywany stały potencjał [math]V_0[/math]?
Zadanie 4
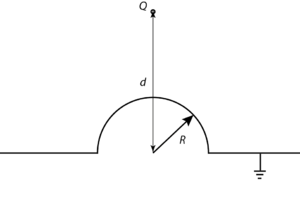
Punktowy ładunek elektryczny o wartości [math]Q[/math] umieszczono w odległości [math]d[/math] od nieskończonej, uziemionej przewodzącej płaszczyzny z „doklejoną” przewodzącą półkulą o promieniu [math]R[/math], na osi symetrii półkuli, tak, jak pokazuje to poniższy rysunek. Znajdź pole elektryczne [math]\vec{E}[/math] oraz potencjał elektryczny [math]V[/math] w całej przestrzeni.