Pracownia EEG/analiza obrazu: Różnice pomiędzy wersjami
| Linia 642: | Linia 642: | ||
from scipy.cluster.vq import kmeans,vq | from scipy.cluster.vq import kmeans,vq | ||
K_opt = 8 | K_opt = 8 | ||
| − | centroids,_ = kmeans(l.ravel(),K_opt) | + | centroids,_ = kmeans(l.ravel()*1.,K_opt) |
# przypisujemy klasę | # przypisujemy klasę | ||
| Linia 659: | Linia 659: | ||
py.show() | py.show() | ||
</source> | </source> | ||
| + | |||
===Segmentacja przez rozrost=== | ===Segmentacja przez rozrost=== | ||
Aktualna wersja na dzień 14:46, 11 sty 2018
Pracownia EEG / Wstęp do analizy obrazu
Spis treści
Wstęp
W tym dziale zajmiemy się analizą obrazu za pomocą narzędzi dostępnych w modułach numpy i scipy. Tak więc na potrzeby tego rozdziału uznamy, że obrazy to dwuwymiarowe tablice numpy. Podstawowe operacje macierzowe będziemy czerpać z modułu numpy zaś bardziej specyficzne operacje z modułu scipy.ndimage.
W dalszym toku zajęć zapoznamy się też częściowo z bardziej dedykowanymi narzędziami zawartymi w module OpenCV.
W poniższych materiałach wykorzystano tutorial: http://scipy-lectures.github.io/advanced/image_processing/#feature-extraction autorstwa: Emmanuelle Gouillart, Gaël Varoquaux.
Wczytywanie i zapisywanie obrazów
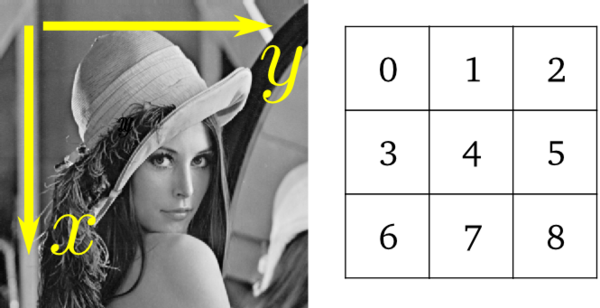
Do wstępnych ćwiczeń posłużymy się standardowym w świecie analizy obrazów zdjęciem znanym jako Lena. Przygotujemy plik w formacie png:
from scipy import misc
l = misc.lena()
misc.imsave('lena.png', l) # tu używany jest niejawnie moduł do podstawowej pracy z plikami graficznymi (PIL - python image library)
import matplotlib.pyplot as plt
plt.imshow(l)
plt.show()
Aby wczytać obrazek z pliku graficznego jako tablicę:
from scipy import misc
lena = misc.imread('lena.png')
type(lena)
lena.shape, lena.dtype
Zwróćmy uwagę na to, że typem dla obrazków jest uint8 (czyli liczby całkowite z zakresu 0-255).
Wyświetlanie obrazów
W tym celu można zastosować funkcję imshow z matplotlib. Zwróćmy uwagę jak ustawia się mapę kolorów.
l = misc.lena()
import matplotlib.pyplot as plt
plt.imshow(l, cmap=plt.cm.gray)
Sterowanie kontrastem za pomocą ustawiania minimalnej i maksymalnej wartości dla skali jasności.
plt.imshow(l, cmap=plt.cm.gray, vmin=30, vmax=200)
# Remove axes and ticks
plt.axis('off')
Aby oglądać obraz z dokładnością do piksela należy zmienić domyślną interpolację, porównajmy dwie wersje:
plt.subplot(1,2,1)
plt.imshow(l[200:220, 200:220], cmap=plt.cm.gray)
plt.subplot(1,2,2)
plt.imshow(l[200:220, 200:220], cmap=plt.cm.gray, interpolation='nearest')
plt.show()
Podstawowe manipulacje
Ponieważ traktujemy obraz jako tablicę numpy możemy stosować standardowe operacje:
lena = scipy.misc.lena()
# adresowanie pojedynczego piksela
lena[0, 40]
# wycinki
lena[10:13, 20:23]
lena[100:120] = 255
lx, ly = lena.shape
X, Y = np.ogrid[0:lx, 0:ly]
mask = (X - lx / 2) ** 2 + (Y - ly / 2) ** 2 > lx * ly / 4
# maskowanie
lena[mask] = 0
# średnia wartość jasności w obrazie, maksimum i minimum
lena.mean()
lena.max()
lena.min()
#przycinanie
crop_lena = lena[lx / 4: - lx / 4, ly / 4: - ly / 4]
# up <-> down flip
flip_ud_lena = np.flipud(lena)
# obroty
rotate_lena = ndimage.rotate(lena, 45)
rotate_lena_noreshape = ndimage.rotate(lena, 45, reshape=False)
Częstość w obrazie i dwuwymiarowa transformata Fouriera
sin 2D
Aby uświadomić sobie związki między jednowymiarowym sygnałem a obrazem — sygnałem 2D — zrobimy następujące ćwiczenie (poniżej prezentowane fragmenty kodu dopisujemy do jednego pliku):
- Zrobimy sinusa jednowymiarowego o 10 okresach na 100 punktów:
# -*- coding: utf-8 -*-
import matplotlib.pyplot as py
import numpy as np
X = 100 #pikseli
Fs = 1.0/X #czestosc probkowania co jeden piksel
dx = 1
x = np.arange(0,X,dx)
f = 10.0/X # czestosc sinusa -10 okresów na X
syg = np.sin(2*np.pi*f*x + np.pi/3);
py.figure(1)
py.plot(x,syg)
py.show()
- Teraz przekształcimy go w obraz:
py.figure(2)
# teraz zrobimy z niego obraz 2D
Y = X/2
SYG = np.zeros((Y,X));
for y in range(Y):
SYG[y,:]=syg
py.subplot(2,2,1)
py.pcolor(SYG, cmap=py.cm.gray,vmin=-2,vmax = 2)
py.show()
Te zmieniające intensywność prążki to właśnie obrazek przedstawiający sin w kierunku X.
Transformata Fouriera 2D
- fft2 z sin2D
py.subplot(221)
py.pcolor(SYG, cmap=py.cm.gray,vmin=-2,vmax = 2)
py.subplot(222)
SK_X = np.arange(-X/2,X/2,1)
SK_Y = np.arange(-Y/2,Y/2,1)
S = np.fft.fft2(SYG)
modS = np.abs(np.fft.fftshift(S))
py.pcolor(SK_X,SK_Y, modS, cmap=py.cm.gray)
- sprawdźmy jak widoczne jest dodanie stałej wartości do obrazu:
py.subplot(223)
py.pcolor(SYG+1, cmap=py.cm.gray, vmin=-2,vmax = 2)
py.subplot(224)
S = np.fft.fft2(SYG+1)
py.pcolor(SK_X,SK_Y,np.abs(np.fft.fftshift(S)), cmap=py.cm.gray)
py.show()
Filtrowanie liniowe. Korelacja i splot
Sygnały jednowymiarowe, np. jeden kanał sygnału EEG, filtrowaliśmy poprzez splatanie sygnału z funkcją odpowiedzi impulsowej filtru. Podobnie można myśleć o filtrowanie obrazów, traktowanych jako sygnały dwuwymiarowe. Trzeba tylko określić jak liczyć splot w dwóch wymiarach. Zobaczmy jak to się robi praktycznie.
Korelacja
Przyjmijmy, że:
- obrazem jest duża macierz;
- jądrem splotu/korelacji jest mniejsza macierz.
Załóżmy, że mamy obraz A:
[[17, 24, 1, 8, 15], [23, 5, 7, 14, 16], [ 4, 6, 13, 20, 22], [10, 12, 19, 21, 3], [11, 18, 25, 2, 9]]
i jądro korelacji h:
[[8, 1, 6], [3, 5, 7], [4, 9, 2]])
wówczas operacja korelacji dla elementu A[1,3] jest następująca:
- kładziemy macierz h elementem środkowym (5) na elemencie A[1,3];
- wymnażamy przez siebie wszystkie pokrywające się elementy i sumujemy iloczyny.
Wtedy dla tego elementu otrzymujemy:
D[1,3] =1*8 + 8*1 +15*6 +
7*3 + 14*5 + 16*7+
13*4 + 20*9 +22*2 = 585
Taką korelację mamy zaimplementowaną w ndimage.correlate (w dokumentacji można doczytać różne opcje dotyczące traktowania brzegów, kiedy macierz h "wystaje" poza macierz A) :
A = np.array([[17, 24, 1, 8, 15],[23, 5, 7, 14, 16 ],[4,6,13,20,22],[10,12,19,21,3],[11,18,25,2,9] ])
h = np.array([[8,1,6],[3,5,7],[4,9,2]])
D = ndimage.correlate(A,h)
Splot
Bardzo podobna jest operacja dwuwymiarowego splotu. Jedyna różnica jest taka, że przed operacją mnożenia i dodawania jądro jest obracane o 180°, implementacja w ndimage.convolve.
Ćwiczenie
Na obrazie lena proszę sprawdzić działanie kilku podstawowych, często stosowanych filtrów:
- filtr uśredniający:
h = np.array([[1./9, 1./9, 1./9],
[1./9, 1./9, 1./9],
[1./9, 1./9, 1./9]])
- filtr wyostrzający:
h = np.array([[ 0, -1, 0],
[ -1, 5, -1],
[ 0, -1, 0]])
- filtr uwypuklający:
h = np.array([[-1, -1, -1, -1, 0],
[ -1, -1, -1, 0, 1],
[ -1, -1, 0, 1, 1],
[ -1, 0, 1, 1, 1],
[ 0, 1, 1, 1, 1]])
Filtry nieliniowe
Koncepcję filtrowania można rozszerzyć na inne operacje wykonywane na pikselach otaczających aktualnie rozważany. Może to być obliczenie dowolnej funkcji z wartości pikseli w sąsiedztwie, np.: mediany, maximum, minimum, konkretnego kwantyla, odchylenia standardowego, zakresu zmienności itd. Dla przykładu rozważmy odszumianie obrazu.
Odszumianie
Szum w obrazie polegający na tym, że wartość każdego piksela jest zaburzona przez wartość losową ma głównie wysokie częstości przestrzenne. W pierwszym podejściu można próbować usunąć je przez filtr uśredniający. Będzie on niestety rozmywał krawędzie. Zwykle lepsze rezultaty daje filtr medianowy (do elementu centralnego przypisywana jest wartość mediany z sąsiedztwa o zadanym promieniu). Proszę porównać:
from scipy import misc
l = misc.lena()
l = l[230:310, 210:350]
noisy = l + 0.4 * l.std() * np.random.random(l.shape)
# dodajmy jeszcze "zagniecenie" zdjęcia
noisy[range(80),range(80)]=255
#filtr gaussowski
gauss_denoised = ndimage.gaussian_filter(noisy, 2)
#filtr medianowy
med_denoised = ndimage.median_filter(noisy, 3)
Operacje morfologiczne
Szczególnym przypadkiem filtrów nieliniowych sa operacje morfologiczne. Polegają one na tym, że obraz jest "próbkowany" pewnym prostym kształtem tzw. elementem strukturalnym. Obraz wyjściowy jest modyfikowany w zależności od tego jak taki element "pasuje" do poszczególnych miejsc obrazu wejściowego. Dalej zajmiemy się operacjami morfologicznymi dla obrazów binarnych.
Element strukturalny
Element strukturalny to binarna maska przykładana do oryginalnego obrazka.
Erozja
Erozja powoduje zamianę aktualnego piksela na wartość minimalną zawartą w części wspólnej elementu strukturalnego o środku w aktualnym pikselu i oryginalnego obrazka.
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as py
from scipy import ndimage
from scipy import misc
def element():
el = np.array([[0, 1, 0],[1,1,1],[0,1,0]], dtype=bool)
#el = np.array([[0, 0, 0],[1,1,1],[0,0,0]], dtype=bool)
return el
def dodaj_kwadrat(ob, x,y, dx,dy):
'''dodaje kwadrat wypełniony 1 do obrazu binarnego ob.
x, y - lewy górny róg
dx,dy - szerokosć i wysokość '''
ob[x:x+dx,y:y+dy] = 1
return ob
def dodaj_kolo(ob, x,y, r):
'''dodaje koło wypełnione 1 do obrazu binarnego ob.
x, y - środek
r - promień '''
r2=r**2
for xi in range(ob.shape[0]):
for yi in range(ob.shape[1]):
if (xi-x)**2+(yi-y)**2<=r2:
ob[xi,yi]=1
return ob
NX=10
NY=10
py.figure('erozja 1')
ob = np.zeros((NX,NY))
py.subplot(1,3,1)
el = element()
py.imshow(el,interpolation = 'nearest',cmap=py.cm.gray)
py.xlim([-0.5,NX])
py.ylim([-0.5,NY])
py.axis('off')
py.title('element strukturalny')
py.subplot(1,3,2)
ob = dodaj_kwadrat(ob,2,2,6,6)
py.imshow(ob, interpolation = 'nearest',cmap=py.cm.gray)
py.xlim([-0.5,NX])
py.ylim([-0.5,NY])
py.axis('off')
py.title(u'obraz wejściowy')
py.subplot(1,3,3)
ob_wyj = ndimage.binary_erosion(ob, structure = el).astype(ob.dtype)
py.imshow(ob_wyj, interpolation = 'nearest',cmap=py.cm.gray)
py.xlim([-0.5,NX])
py.ylim([-0.5,NY])
py.axis('off')
py.title(u'obraz wyjściowy')
py.show()
py.figure('erozja 2')
ob = np.zeros((NX,NY))
py.subplot(1,3,1)
el = element()
py.imshow(el,interpolation = 'nearest',cmap=py.cm.gray)
py.xlim([-0.5,NX])
py.ylim([-0.5,NY])
py.axis('off')
py.title('element strukturalny')
py.subplot(1,3,2)
#ob = dodaj_kwadrat(ob,2,2,6,6)
ob = dodaj_kolo(ob,5,5,3)
py.imshow(ob, interpolation = 'nearest',cmap=py.cm.gray)
py.xlim([-0.5,NX])
py.ylim([-0.5,NY])
py.axis('off')
py.title(u'obraz wejściowy')
py.subplot(1,3,3)
ob_wyj = ndimage.binary_erosion(ob, structure = el).astype(ob.dtype)
py.imshow(ob_wyj, interpolation = 'nearest',cmap=py.cm.gray)
py.xlim([-0.5,NX])
py.ylim([-0.5,NY])
py.axis('off')
py.title(u'obraz wyjściowy')
py.show()
Dylacja
Dylacja powoduje zamianę aktualnego piksela na wartość maksymalną zawartą w części wspólnej elementu strukturalnego o środku w aktualnym pikselu i oryginalnego obrazka. Implementacja: ndimage.binary_dilation. Proszę wypróbować tą operację modyfikując kod przykładowy od Erozji.
Otwarcie
Otwarcie to złożenie operacji erozji i dylacji. Operacja otwarcia zachowuje rozmiary obiektów obrazu przy ich jednoczesnym wygładzeniu — usunięciu wszystkich „wystających” elementów. Zwiększanie rozmiaru elementu strukturalnego B skutkuje usuwaniem coraz większych detali obrazu oraz upodabnianiem powstałych obszarów do elemetu strukturalnego. Implementacja: ndimage.binary_opening. Proszę wypróbować tą operację:
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as py
from scipy import ndimage
from scipy import misc
def element():
#el = np.array([[0, 1, 0],[1,1,1],[0,1,0]], dtype=bool)
el = np.zeros((3,3))
el = dodaj_kolo(el,1.5,1.5,1.5)
return el
def dodaj_kwadrat(ob, x,y, dx,dy):
'''dodaje kwadrat wypełniony 1 do obrazu binarnego ob.
x, y - lewy górny róg
dx,dy - szerokosć i wysokość '''
ob[x:x+dx,y:y+dy] = 1
return ob
def dodaj_kolo(ob, x,y, r):
'''dodaje koło wypełnione 1 do obrazu binarnego ob.
x, y - środek
r - promień '''
r2=r**2
for xi in range(ob.shape[0]):
for yi in range(ob.shape[1]):
if (xi-x)**2+(yi-y)**2<=r2:
ob[xi,yi]=1
return ob
def dodaj_szum(ob,ile):
tmp = np.random.rand(ob.shape[0],ob.shape[1])
idx = np.where(tmp<ile)
ob[idx] = np.abs(ob[idx]-1)
return ob
py.close('all')
NX=100
NY=100
#spróbujmy progowania na różnym poziomie
py.figure('erozja 1')
ob = np.zeros((NX,NY))
py.subplot(1,3,1)
el = element()
py.imshow(el,interpolation = 'nearest',cmap=py.cm.gray)
py.xlim([-0.5,NX])
py.ylim([-0.5,NY])
py.axis('off')
py.title('element strukturalny')
py.subplot(1,3,2)
ob = dodaj_kwadrat(ob,20,20,60,60)
ob = dodaj_szum(ob,0.2)
py.imshow(ob, interpolation = 'nearest',cmap=py.cm.gray)
py.xlim([-0.5,NX])
py.ylim([-0.5,NY])
py.axis('off')
py.title(u'obraz wejściowy')
py.subplot(1,3,3)
ob_wyj = ndimage.binary_opening(ob, structure = el).astype(ob.dtype)
py.imshow(ob_wyj, interpolation = 'nearest',cmap=py.cm.gray)
py.xlim([-0.5,NX])
py.ylim([-0.5,NY])
py.axis('off')
py.title(u'obraz wyjściowy')
py.show()
py.figure('erozja 2')
ob = np.zeros((NX,NY))
py.subplot(1,3,1)
el = element()
py.imshow(el,interpolation = 'nearest',cmap=py.cm.gray)
py.xlim([-0.5,NX])
py.ylim([-0.5,NY])
py.axis('off')
py.title('element strukturalny')
py.subplot(1,3,2)
#ob = dodaj_kwadrat(ob,2,2,6,6)
ob = dodaj_kolo(ob,50,50,30)
ob = dodaj_szum(ob,0.2)
py.imshow(ob, interpolation = 'nearest',cmap=py.cm.gray)
py.xlim([-0.5,NX])
py.ylim([-0.5,NY])
py.axis('off')
py.title(u'obraz wejściowy')
py.subplot(1,3,3)
ob_wyj = ndimage.binary_opening(ob, structure = el).astype(ob.dtype)
py.imshow(ob_wyj, interpolation = 'nearest',cmap=py.cm.gray)
py.xlim([-0.5,NX])
py.ylim([-0.5,NY])
py.axis('off')
py.title(u'obraz wyjściowy')
py.show()
Domknięcie
Domknięcie to złożenie operacji dylacji i erozji. Domknięcie usuwa z obrazu wszelkie „dziury” oraz wklęsłości mniejsze od elementu strukturalnego. Może skutkować „połączeniem się” blisko położonych detali. Zwiększanie wielkości elementu strukturalnego powoduje wypełnianie coraz większych „dziur” oraz wklęsłości, upodabnianiem powstałych obszarów do elementu strukturalnego i łączeniem coraz dalej położonych detali.Implementacja: ndimage.binary_closing. Proszę wypróbować tą operację modyfikując poprzedni skrypt.
Progowanie
Aby uzyskać obraz binarny z obrazu w skali szarości należy obraz wejściowy sprogować. Proszę obejrzeć histogram szarości Leny i zobaczyć efekty progowania dla kilku wybranych wartości:
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as py
from scipy import ndimage
from scipy import misc
def proguj(ob, prog):
ob_wyj = np.zeros(ob.shape)
ob_wyj[np.where(ob>prog)]=1
return ob_wyj
py.close('all')
l = misc.lena()
py.figure('histogram szarosci')
py.hist(l.ravel(),255) # narysujmy histogram odcieni
py.show()
#spróbujmy progowania na różnym poziomie
py.figure('progowanie')
py.subplot(1,2,1)
py.imshow(l,interpolation = 'nearest',cmap=py.cm.gray)
py.axis('off')
py.subplot(1,2,2)
prog = 110
l_prog = proguj(l,prog)
py.imshow(l_prog, interpolation = 'nearest',cmap=py.cm.gray)
py.axis('off')
py.show()
Szukanie krawędzi
Złożenie operacji morfologicznych erozji i dylacji można zastosować do detekcji krawędzi.
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as py
from scipy import ndimage
from scipy import misc
def proguj(ob, prog):
ob_wyj = np.zeros(ob.shape)
ob_wyj[np.where(ob>prog)]=1
return ob_wyj
def element():
#el = np.array([[0, 1, 0],[1,1,1],[0,1,0]], dtype=bool)
el = np.zeros((6,6))
el = dodaj_kolo(el,3,3,3)
return el
def dodaj_kwadrat(ob, x,y, dx,dy):
'''dodaje kwadrat wypełniony 1 do obrazu binarnego ob.
x, y - lewy górny róg
dx,dy - szerokosć i wysokość '''
ob[x:x+dx,y:y+dy] = 1
return ob
def dodaj_kolo(ob, x,y, r):
'''dodaje koło wypełnione 1 do obrazu binarnego ob.
x, y - środek
r - promień '''
r2=r**2
for xi in range(ob.shape[0]):
for yi in range(ob.shape[1]):
if (xi-x)**2+(yi-y)**2<=r2:
ob[xi,yi]=1
return ob
py.close('all')
l = misc.lena()
py.figure('operacje')
py.subplot(3,3,1)
py.imshow(l,interpolation = 'nearest',cmap=py.cm.gray)
py.axis('off')
py.title(u'oryginał')
py.subplot(3,3,2)
prog = 110
l_prog = proguj(l,prog)
py.imshow(l_prog, interpolation = 'nearest',cmap=py.cm.gray)
py.axis('off')
py.title('progowany')
py.subplot(3,3,3)
el=element()
l_wyj1 = ndimage.binary_erosion(l_prog, structure = el).astype(l_prog.dtype)
py.imshow(l_wyj1, interpolation = 'nearest',cmap=py.cm.gray)
py.axis('off')
py.title('erozja')
py.subplot(3,3,6)
el=element()
l_wyj2 = ndimage.binary_dilation(l_prog, structure = el).astype(l_prog.dtype)
py.imshow(l_wyj2, interpolation = 'nearest',cmap=py.cm.gray)
py.axis('off')
py.title('dylacja')
py.subplot(3,3,9)
l_wyj3 = l_wyj2-l_wyj1
py.imshow(l_wyj3, interpolation = 'nearest',cmap=py.cm.gray)
py.axis('off')
py.title('erozja-dylacja')
py.subplot(3,3,8)
el = np.array([[0, 1, 0],[1,1,1],[0,1,0]], dtype=bool)
l_wyj3 = ndimage.binary_erosion(l_prog, structure = el).astype(l_prog.dtype)-ndimage.binary_dilation(l_prog, structure = el).astype(l_prog.dtype)
py.imshow(l_wyj3, interpolation = 'nearest',cmap=py.cm.gray)
py.axis('off')
py.title(u'erozja-dylacja,mały element')
py.subplot(3,3,4)
l_wyj4 = ndimage.binary_closing(l_prog, structure = el).astype(l_prog.dtype)
py.imshow(l_wyj4, interpolation = 'nearest',cmap=py.cm.gray)
py.axis('off')
py.title(u'domknięcie')
py.subplot(3,3,5)
l_wyj5 = ndimage.binary_opening(l_prog, structure = el).astype(l_prog.dtype)
py.imshow(l_wyj5, interpolation = 'nearest',cmap=py.cm.gray)
py.axis('off')
py.title(u'otwarcie')
py.show()
Segmentacja
Na początek, do treningu wytworzymy obrazek zawierający kilka obiektów.
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as py
from scipy import ndimage
from scipy import misc
np.random.seed(1)
n = 10
l = 256
# generujemy pusty obrazek
im = np.zeros((l, l))
# w losowych miejscach dorzucamy n punktów
points = l*np.random.random((2, n**2))
im[(points[0]).astype(np.int), (points[1]).astype(np.int)] = 1
#rozmywamy punkty filtrem gaussowskim
im = ndimage.gaussian_filter(im, sigma=l/(4.*n))
#progujemy maskę na połowie wartości średniej obrazka
mask = (im > im.mean()).astype(np.float)
# wytwarzamy obrazek złożony z zaszumionej maski
img = mask + 0.2*np.random.randn(*mask.shape)
#progujemy zszumiony obrazek
binary_img = img > 0.5
hist, bin_edges = np.histogram(img, bins=60)
bin_centers = 0.5*(bin_edges[:-1] + bin_edges[1:])
py.figure(figsize=(11,4))
py.subplot(131)
py.imshow(img)
py.axis('off')
py.subplot(132)
#py.plot(bin_centers, hist, lw=2)
py.hist(img.ravel(),60)
py.axvline(0.5, color='r', ls='--', lw=2)
py.yticks([])
py.subplot(133)
py.imshow(binary_img, cmap=py.cm.gray, interpolation='nearest')
py.axis('off')
py.show()
Segmentacja za pomocą funkcji ndimage.label
# odszumiamy
# usuwamy białe kropki
open_img = ndimage.binary_opening(binary_img)
py.subplot(234)
py.imshow(open_img)
py.axis('off')
# usuwamy małe czarne dziury
close_img = ndimage.binary_closing(open_img)
py.subplot(235)
py.imshow(close_img)
py.axis('off')
# segmentujemy:
img_labeled,N_objects = ndimage.label(close_img)
py.subplot(236)
py.imshow(img_labeled.astype(np.float),interpolation='nearest')
py.colorbar()
py.axis('off')
py.title(str(N_objects)+u' obiektów')
py.show()
Segmentacja przez analizę skupień (k-means)
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as py
from scipy import ndimage
from scipy import misc
#segmentacja przez analizę skupień
l=misc.lena()
from scipy.cluster.vq import kmeans,vq
K_opt = 8
centroids,_ = kmeans(l.ravel()*1.,K_opt)
# przypisujemy klasę
idx,_ = vq(l.ravel(),centroids)
idx.shape = l.shape
py.figure(2)
py.subplot(1,2,1)
py.imshow(idx)#, cmap=py.cm.gray)
py.colorbar()
py.axis('off')
py.subplot(1,2,2)
tmp_obj = np.zeros((l.shape[0],l.shape[1]))
tmp_obj[np.where(idx==4)] = 1
py.imshow(tmp_obj)#, cmap=py.cm.gray)
py.axis('off')
py.show()
Segmentacja przez rozrost
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as py
from scipy import ndimage
from scipy import misc
import sys
#segmentacja przez rozrost
def testuj(reg_id, x,y, do_sprawdzenia, prog = 10):
global im_org, im_marked, reg_wsp, reg_wart
while len(do_sprawdzenia)>0:
tmp_x,tmp_y = do_sprawdzenia.pop(0)
#print 'testuje: ', tmp_x,tmp_y
if tmp_x>=0 and tmp_y>=0 and tmp_x<im_org.shape[0] and tmp_y<im_org.shape[1]: # jeśli punkt wewnątrz obrazu
if im_marked[tmp_x,tmp_y]==-1: # jeśli punkt nie należy do żadnego regionu
if im_marked[tmp_x,tmp_y] != reg_id: #jeśli punkt nie należy do aktualnego regionu
if np.abs(im_org[tmp_x,tmp_y]-np.mean(reg_wart[reg_id])) < prog: #jeśli punkt ma wartość bliższą do średniej z obszaru niż próg
#to dodajemy punkt do listy bieżącego regionu, odhaczamy go na mapie regionów i dodajemy jego sąsiadów do listy, którą trzeba sprawdzić
reg_wsp[reg_id].append((tmp_x,tmp_y))
reg_wart[reg_id].append(im_org[tmp_x,tmp_y])
im_marked[tmp_x,tmp_y]=reg_id
do_sprawdzenia.append((tmp_x-1,tmp_y))
do_sprawdzenia.append((tmp_x ,tmp_y+1))
do_sprawdzenia.append((tmp_x, tmp_y-1))
do_sprawdzenia.append((tmp_x+1,tmp_y))
return do_sprawdzenia
# wczytujemy lenę i wybieramy fragment z twarzą
l=misc.lena()
l = np.copy(l[200:400,200:400])
global im_org, im_marked, reg_wsp, reg_wart
im_marked = -1*np.ones((l.shape[0],l.shape[1]),dtype='int')
im_org = l
# próg na odchylenie dołączanego punktu od średniej
prog = 35
reg_wsp = []
reg_wart =[]
reg_id = 0
while np.sum(im_marked==-1)>0:
# współrzędne punktu startowego bierzemy jako pierwsze z brzegu nie przypisane jeszcze do żadnego regionu
x=np.where(im_marked==-1)[0][0]
y=np.where(im_marked==-1)[1][0]
# dodajemy miejsce na listę przechowującą współrzedne punktów należących do regionów i na ich wartości
reg_wsp.append([])
reg_wsp[reg_id].append((x,y))
reg_wart.append([])
reg_wart[reg_id].append(im_org[x,y])
# odchaczamy na mapie regionów bieżący punkt jako przypisany do reg_id
im_marked[x,y] = reg_id
# inicjujemy listę punktów, które trzeba sprawdzić, czy nie należą do bieżącego regionu
do_sprawdzenia = [(x-1,y),(x,y+1),(x,y-1),(x+1,y)]
do_sprawdzenia = testuj(reg_id,x,y,do_sprawdzenia,prog)
print reg_id
reg_id +=1
# rysowanie wyników
py.figure(2)
py.subplot(1,3,1)
py.imshow(l, interpolation='nearest', cmap=py.cm.gray)
py.axis('off')
py.title(u'oryginał')
py.subplot(1,3,2)
py.imshow(im_marked, interpolation='nearest')#, cmap=py.cm.gray)
py.axis('off')
py.title('po segmentacji')
py.subplot(1,3,3)
S = np.array([ len(reg_wart[i]) for i in range(len(reg_wart))])
id = np.where((S>5000))[0][0]
py.imshow(im_marked==id, interpolation='nearest')#, cmap=py.cm.gray)
py.axis('off')
py.title('obiekt '+str(id))
py.show()
Zadanie
Przygotuj prezentację demonstrującą działanie operacji na obrazach omawianych w tym rozdziale. Zademonstruj różne możliwości użytych operacji (np. usuwanie drobnych szczegółów z obrazu lub dużych struktur, itp.). Zaproponuj odpowiednio dobrane własne obrazy, aby lepiej uwidocznić uzyskane efekty.