WnioskowanieStatystyczne/Effect size: Różnice pomiędzy wersjami
| (Nie pokazano 13 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 3: | Linia 3: | ||
==Wielkość efektu (''Effect size'')== | ==Wielkość efektu (''Effect size'')== | ||
| − | to | + | to ilościowa miara siły zjawiska. |
| − | |||
Głównym, spójnym i eleganckim celem omawiawianych dotychczas metod było przejście z różnorodności mierzonych eksperymentalnie wielkości — milimetry, lata świetlne, tony, stopnie Celsjusza — do uniwersalnej i bezwymiarowej wielkości prawdopodobieństwa <math>p</math>. Jednak ogólnie wskazane jest utrzymywanie kontaktu z rzeczywistością fizyczną, z której pochodzą zarówno pomiary jak i hipotezy. Dla wyjaśnienia rozważmy prosty przykład: ''Na bardzo dużej grupie pacjentów udowadniamy, że nowy lek w stanach zapalnych zmniejsza temperaturę silniej niż aspiryna. Efekt jest istotny statystycznie na poziomie 1%.'' Czy to wszystko? | Głównym, spójnym i eleganckim celem omawiawianych dotychczas metod było przejście z różnorodności mierzonych eksperymentalnie wielkości — milimetry, lata świetlne, tony, stopnie Celsjusza — do uniwersalnej i bezwymiarowej wielkości prawdopodobieństwa <math>p</math>. Jednak ogólnie wskazane jest utrzymywanie kontaktu z rzeczywistością fizyczną, z której pochodzą zarówno pomiary jak i hipotezy. Dla wyjaśnienia rozważmy prosty przykład: ''Na bardzo dużej grupie pacjentów udowadniamy, że nowy lek w stanach zapalnych zmniejsza temperaturę silniej niż aspiryna. Efekt jest istotny statystycznie na poziomie 1%.'' Czy to wszystko? | ||
| − | Może się okazać, że (istotna) różnica między średnim spadkiem temperatury w grupach przyjmujących aspirynę i placebo wyniosła 0,05 stopnia Celsjusza. W tym przypadku intuicja podpowiada, że zmiana — pomimo, że istotna statystycznie — jest bardzo niewielka, i na pewno inaczej podchodzilibyśmy do leku, który daje | + | Może się okazać, że (istotna) różnica między średnim spadkiem temperatury w grupach przyjmujących aspirynę i placebo wyniosła 0,05 stopnia Celsjusza. W tym przypadku intuicja podpowiada, że zmiana — pomimo, że istotna statystycznie — jest bardzo niewielka, i na pewno inaczej podchodzilibyśmy do leku, który daje różnicę średnich np. 2 stopni Celsjusza przy tym samym <math>p</math>. W ogólnym przypadku taką intuicją nie dysponujemy, stąd rozmaitość różnych i niezbyt spójnych miar (według [https://en.wikipedia.org/wiki/Effect_size Wikipedii] jest ich kiladziesiąt), które mają ten efekt kwantyfikować w sposób możliwie uniwersalny. Przyjrzyjmy się krytycznie niektórym przykładom pamiętając, że raportowanie tego efektu jest coraz częściej wymagane w publikacjach wyników badawczych. |
| Linia 14: | Linia 13: | ||
:<math>d=\frac{\bar{x}_1 - \bar{x}_2}{s}.</math> | :<math>d=\frac{\bar{x}_1 - \bar{x}_2}{s}.</math> | ||
| − | Coż, można by mówić po prostu "różnica średnich podzielona przez wariancję". Jednak kwestia raportowania tego efektu | + | Coż, można by mówić po prostu "różnica średnich podzielona przez wariancję". Jednak kwestia raportowania tego efektu pojawiła się najpierw w psychologii — [https://pl.wikipedia.org/wiki/Jacob_Cohen Jacob Cohen], od którego nazwiska pochodzą nazwy zaproponowanych przez niego miar, był psychologiem i statystykiem. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | {| class="wikitable" | + | {| class="wikitable floatright" style="border:20px solid white;background:white" |
!| ''Effect size'' || ''d'' | !| ''Effect size'' || ''d'' | ||
|- | |- | ||
| Linia 36: | Linia 31: | ||
|- | |- | ||
|} | |} | ||
| + | Na przykład tabela po prawej podsumowuje rekomendacje z artykułów | ||
| + | ''<small>Cohen, Jacob (1988). Statistical Power Analysis for the Behavioral Sciences. Routledge. ISBN 978-1-134-74270-7</small>'' i ''<small>Sawilowsky, S (2009). "New effect size rules of thumb". Journal of Modern Applied Statistical Methods. 8 (2): 467–474. doi:10.22237/jmasm/1257035100</small>''. Do tej "klasyfikacji" należy oczywiście podchodzić z dystansem, jak sugerował sam Cohen (również dlatego, że nawet sposób estymacji wariancji w mianowniku nie jest ustalony:): | ||
| + | <blockquote>''The terms 'small,' 'medium,' and 'large' are relative, not only to each other, but to the area of behavioral science or even more particularly to the specific content and research method being employed in any given investigation... In the face of this relativity, there is a certain risk inherent in offering conventional operational definitions for these terms for use in power analysis in as diverse a field of inquiry as behavioral science. This risk is nevertheless accepted in the belief that more is to be gained than lost by supplying a common conventional frame of reference which is recommended for use only when no better basis for estimating the ES index is available.''</blockquote> | ||
| + | |||
| + | ==== Współczynnik korelacji ''r'' Pearsona ==== | ||
| + | {| class="wikitable" style="border:20px solid white;background:white" | ||
| + | ! ''r'' | ||
| + | ! Effect size | ||
| + | |- | ||
| + | | 0,10 | ||
| + | | Small | ||
| + | |- | ||
| + | | 0,30 | ||
| + | | Medium | ||
| + | |- | ||
| + | | 0,50 | ||
| + | | Large | ||
| + | |} | ||
| + | Jak pamiętamy z rozdziału [[WnioskowanieStatystyczne/Interpretacja_współczynnika_korelacji|Interpretacja współczynnika korelacji]], jego kwadrat to po prostu stosunek wariancji wyjaśnianej przez model liniowy. Ale jeśli to dla kogoś za proste, możemy się posłużyć kolejnymi "regułami kciuka" z innej pracy Jacoba Cohena: <small>Statistical Power Analysis for the Behavioral Sciences (second ed.). Lawrence Erlbaum Associates, 1988, s. 590.</small> i <small>A power primer. „Psychological Bulletin”. 112 (1). s. 155–159.</small> | ||
| + | {| class="wikitable" style="border:20px solid white;background:white" | ||
| + | ! ''r'' | ||
| + | ! % VAR | ||
| + | ! Effect size | ||
| + | |- | ||
| + | | 0,10 | ||
| + | | 1% | ||
| + | | Small | ||
| + | |- | ||
| + | | 0,30 | ||
| + | | 9% | ||
| + | | Medium | ||
| + | |- | ||
| + | | 0,50 | ||
| + | | 25% | ||
| + | | Large | ||
| + | |} | ||
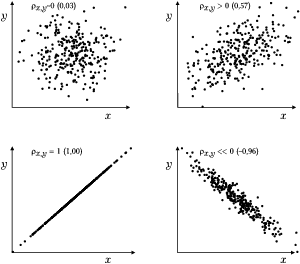
| − | < | + | [[Plik:Korelacja.png|600px|thumb|left|<figure id="fig:rozw2"></figure>Przykładowe wartości współczynnika korelacji dla 300 par <math>(x, y)</math> o |
| + | różnych stopniach współzależności. | ||
| + | ]] | ||
Aktualna wersja na dzień 19:33, 18 maj 2023
Wnioskowanie_Statystyczne_-_wykład
Wielkość efektu (Effect size)
to ilościowa miara siły zjawiska. Głównym, spójnym i eleganckim celem omawiawianych dotychczas metod było przejście z różnorodności mierzonych eksperymentalnie wielkości — milimetry, lata świetlne, tony, stopnie Celsjusza — do uniwersalnej i bezwymiarowej wielkości prawdopodobieństwa [math]p[/math]. Jednak ogólnie wskazane jest utrzymywanie kontaktu z rzeczywistością fizyczną, z której pochodzą zarówno pomiary jak i hipotezy. Dla wyjaśnienia rozważmy prosty przykład: Na bardzo dużej grupie pacjentów udowadniamy, że nowy lek w stanach zapalnych zmniejsza temperaturę silniej niż aspiryna. Efekt jest istotny statystycznie na poziomie 1%. Czy to wszystko? Może się okazać, że (istotna) różnica między średnim spadkiem temperatury w grupach przyjmujących aspirynę i placebo wyniosła 0,05 stopnia Celsjusza. W tym przypadku intuicja podpowiada, że zmiana — pomimo, że istotna statystycznie — jest bardzo niewielka, i na pewno inaczej podchodzilibyśmy do leku, który daje różnicę średnich np. 2 stopni Celsjusza przy tym samym [math]p[/math]. W ogólnym przypadku taką intuicją nie dysponujemy, stąd rozmaitość różnych i niezbyt spójnych miar (według Wikipedii jest ich kiladziesiąt), które mają ten efekt kwantyfikować w sposób możliwie uniwersalny. Przyjrzyjmy się krytycznie niektórym przykładom pamiętając, że raportowanie tego efektu jest coraz częściej wymagane w publikacjach wyników badawczych.
d Cohena
d Cohena jest zdefiniowane jako różnica pomiędzy średnimi podzielona przez odchylenie standardowe w próbie
- [math]d=\frac{\bar{x}_1 - \bar{x}_2}{s}.[/math]
Coż, można by mówić po prostu "różnica średnich podzielona przez wariancję". Jednak kwestia raportowania tego efektu pojawiła się najpierw w psychologii — Jacob Cohen, od którego nazwiska pochodzą nazwy zaproponowanych przez niego miar, był psychologiem i statystykiem.
| Effect size | d |
|---|---|
| Very small | 0.01 |
| Small | 0.20 |
| Medium | 0.50 |
| Large | 0.80 |
| Very large | 1.20 |
| Huge | 2.0 |
Na przykład tabela po prawej podsumowuje rekomendacje z artykułów Cohen, Jacob (1988). Statistical Power Analysis for the Behavioral Sciences. Routledge. ISBN 978-1-134-74270-7 i Sawilowsky, S (2009). "New effect size rules of thumb". Journal of Modern Applied Statistical Methods. 8 (2): 467–474. doi:10.22237/jmasm/1257035100. Do tej "klasyfikacji" należy oczywiście podchodzić z dystansem, jak sugerował sam Cohen (również dlatego, że nawet sposób estymacji wariancji w mianowniku nie jest ustalony:):
The terms 'small,' 'medium,' and 'large' are relative, not only to each other, but to the area of behavioral science or even more particularly to the specific content and research method being employed in any given investigation... In the face of this relativity, there is a certain risk inherent in offering conventional operational definitions for these terms for use in power analysis in as diverse a field of inquiry as behavioral science. This risk is nevertheless accepted in the belief that more is to be gained than lost by supplying a common conventional frame of reference which is recommended for use only when no better basis for estimating the ES index is available.
Współczynnik korelacji r Pearsona
| r | Effect size |
|---|---|
| 0,10 | Small |
| 0,30 | Medium |
| 0,50 | Large |
Jak pamiętamy z rozdziału Interpretacja współczynnika korelacji, jego kwadrat to po prostu stosunek wariancji wyjaśnianej przez model liniowy. Ale jeśli to dla kogoś za proste, możemy się posłużyć kolejnymi "regułami kciuka" z innej pracy Jacoba Cohena: Statistical Power Analysis for the Behavioral Sciences (second ed.). Lawrence Erlbaum Associates, 1988, s. 590. i A power primer. „Psychological Bulletin”. 112 (1). s. 155–159.
| r | % VAR | Effect size |
|---|---|---|
| 0,10 | 1% | Small |
| 0,30 | 9% | Medium |
| 0,50 | 25% | Large |