FT-intuicja: Różnice pomiędzy wersjami
| (Nie pokazano 13 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 1: | Linia 1: | ||
===[[Analiza_sygnałów_-_wykład|⬆]] Intuicyjna intepretacja przekształcenia Fouriera=== | ===[[Analiza_sygnałów_-_wykład|⬆]] Intuicyjna intepretacja przekształcenia Fouriera=== | ||
| + | |||
| + | [[Plik:Dispersive prism.png|400px|zdjęcie pryzmatu]] | ||
| + | [[Plik:Light dispersion conceptual waves.gif|326px|rozszczepienie światła w pryzmacie]] | ||
| + | |||
| + | <br/> | ||
Spróbujmy nabrać potrzebnej na ćwiczeniach intuicji, traktując obliczenia w kategorii iloczynów skalarnych z kolejnymi sinusami o odpowiednio dobranych fazach. Weźmy przykładowy sygnał ''s'' o długości 256 punktów, złożony z dwóch sinusów ''a'' i ''b'', ''s'' = ''a'' + ''b'': | Spróbujmy nabrać potrzebnej na ćwiczeniach intuicji, traktując obliczenia w kategorii iloczynów skalarnych z kolejnymi sinusami o odpowiednio dobranych fazach. Weźmy przykładowy sygnał ''s'' o długości 256 punktów, złożony z dwóch sinusów ''a'' i ''b'', ''s'' = ''a'' + ''b'': | ||
| Linia 32: | Linia 37: | ||
===Rozdzielczość (F)FT=== | ===Rozdzielczość (F)FT=== | ||
| − | + | Przyjrzyjmy się bliżej analizowanemu powyżej 'przykładowemu sygnałowi' | |
| − | + | [[Plik:Ft sig s.png|400px|center|bezramki]] | |
| − | + | Wyrysowana powyżej linia łamana łaczy sąsiednie z kolejnych 256 wartości wektora próbek | |
| − | + | [[Plik:Ft sig digit nounits.png|400px|center|bezramki]] | |
| − | [[Plik:Ft sig digit.png| | + | Poza samym wektorem próbek, do oznaczenia osi na powyższych widmach potrzebna jest informacja o częstości próbkowania oraz przeliczniku wartości kolejnych próbek na wielkości fizyczne (np. mikrowolty). W tym przypadku odstęp między próbkami wynosił <math>\frac{1}{128}</math> sekundy, więc ten wektor jest zapisem dwóch sekund sygnału: |
| + | [[Plik:Ft sig digit.png|420px|center|bezramki]] | ||
| − | Transformata Fouriera jest przedstawieniem sygnału | + | Transformata Fouriera jest przedstawieniem sygnału w bazie złożonej z funkcji <math>e^{i\omega t}</math>. Wymiar tej bazy powinien odpowiadać wymiarowi sygnału. Ponieważ dla każdej częstości zespolona transformata odtwarza amplitudę i fazę, to w widmie mocy będzie dwukrotnie mniej punktów niż w sygnale, dla którego liczono transformatę. Punkty w których liczymy transformatę Fouriera rozkładają się równomiernie od zera do częstości Nyquista, czyli połowy częstości próbkowania. Przy częstości próbkowania 128Hz częstość Nyquista wynosi 64Hz. Liczba punktów w transformacjie Fouriera wynosi tyle, ile w naturalne bazie sygnału, czyli 256. Połowa tych wartości opisuje amplitudy, a druga połowa fazy. Tak więc w widmie amplitudowym będzie 128 punktów, rozłożonych równomiernie od zera do 64 Hz, czyli rozdzielczość widma wyniesie w tym przypadku 0,5Hz. |
| − | Jako przykład spróbujmy rozszyfrować, skąd w przykładowym artykule | + | Jako przykład 'z prawdziwego świata' spróbujmy rozszyfrować, skąd w przykładowym artykule<ref> |
| − | Xiaorong Gao, Dingfeng Xu, Ming Cheng and Shangkai Gao, "A BCI-based environmental controller for the motion-disabled" IEEE Transactions on Neural Systems and Rehabilitation Engineering, vol. 11, no. 2, pp. 137-140, June 2003, doi: 10.1109/TNSRE.2003.814449, https://web.archive.org/web/20091114205637id_/http://www.cis.gsu.edu/brainlab/papers/gao%202003%20-%2048N%20BCI.pdf</ref> pojawiają się dziwne częstości 6,83 i 7,03 Hz. | + | Xiaorong Gao, Dingfeng Xu, Ming Cheng and Shangkai Gao, "A BCI-based environmental controller for the motion-disabled" IEEE Transactions on Neural Systems and Rehabilitation Engineering, vol. 11, no. 2, pp. 137-140, June 2003, doi: 10.1109/TNSRE.2003.814449, https://web.archive.org/web/20091114205637id_/http://www.cis.gsu.edu/brainlab/papers/gao%202003%20-%2048N%20BCI.pdf</ref> o interfejsach mózg-komputer opartych o [https://youtu.be/xXgZHQopgxM SSVEP] pojawiają się dziwne częstości 6,83 i 7,03 Hz. |
Mamy tam do czynienia z 3-sekundowymi odcinkami sygnału próbkowanego z częstością 200Hz. Aby umożliwić stosowanie szybkiej transformaty Fouriera (FFT) oraz zwiększyć rozdzielczość, sygnał jest dopełniany (zerami) do 1024 punktów. | Mamy tam do czynienia z 3-sekundowymi odcinkami sygnału próbkowanego z częstością 200Hz. Aby umożliwić stosowanie szybkiej transformaty Fouriera (FFT) oraz zwiększyć rozdzielczość, sygnał jest dopełniany (zerami) do 1024 punktów. | ||
| Linia 51: | Linia 57: | ||
<references /> | <references /> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <div align="right"> | ||
| + | [[Przekształcenie_Fouriera|⬅]] [[Analiza_sygnałów_-_wykład|⬆]] [[Twierdzenia_o_splocie_i_o_próbkowaniu_(aliasing)|⮕]] | ||
| + | </div> | ||
Aktualna wersja na dzień 07:31, 18 paź 2024
⬆ Intuicyjna intepretacja przekształcenia Fouriera
Spróbujmy nabrać potrzebnej na ćwiczeniach intuicji, traktując obliczenia w kategorii iloczynów skalarnych z kolejnymi sinusami o odpowiednio dobranych fazach. Weźmy przykładowy sygnał s o długości 256 punktów, złożony z dwóch sinusów a i b, s = a + b:
=
+
Bazą będzie zbiór ortogonalnych sinusów[math]f(x)=\sin(kx), k=1,2,\ldots[/math] o częstościach od [math]\frac{1}{\mathrm{długość \, sygnału}}[/math] do częstości Nyquista.
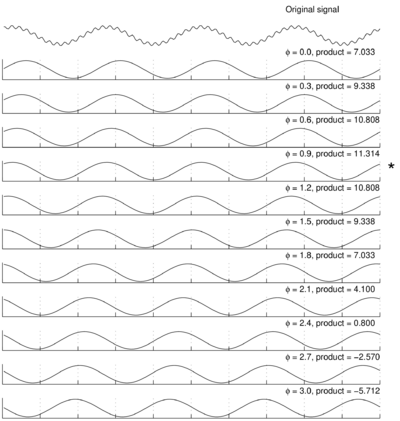
Policzmy iloczyny z sinusami o optymalnie dobranych fazach; jak widać na poniższym rysunku, sinus o częstości 2,4 jest podobny do składowej a sygnału s, ale miara podobieństwa, czyli wartość iloczynu skalarnego, zależy silnie od fazy sinusa, z którym liczymy iloczyn sygnału — gwiazdką oznaczyliśmy fazę, dla której iloczyn jest największy:
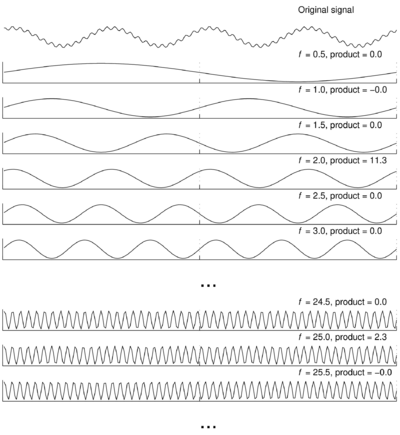
Podobne dopasowania można wykonać dla każdej częstości wzajemnie ortogonalnych sinusów o częstościach [math] \frac1T, \frac2T, \ldots[/math] do częstości Nyquista.
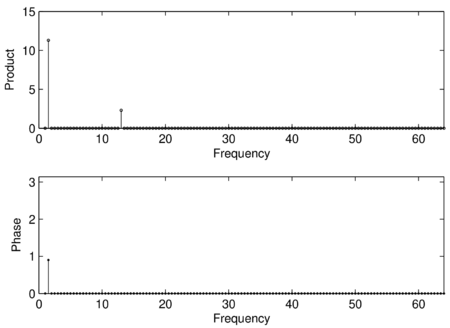
Wyniki — optymalne fazy i uzyskane dla nich maksymalne wartości iloczynów skalarnych — przedstawiamy na wykresach:
Rozdzielczość (F)FT
Przyjrzyjmy się bliżej analizowanemu powyżej 'przykładowemu sygnałowi'
Wyrysowana powyżej linia łamana łaczy sąsiednie z kolejnych 256 wartości wektora próbek
Poza samym wektorem próbek, do oznaczenia osi na powyższych widmach potrzebna jest informacja o częstości próbkowania oraz przeliczniku wartości kolejnych próbek na wielkości fizyczne (np. mikrowolty). W tym przypadku odstęp między próbkami wynosił [math]\frac{1}{128}[/math] sekundy, więc ten wektor jest zapisem dwóch sekund sygnału:
Transformata Fouriera jest przedstawieniem sygnału w bazie złożonej z funkcji [math]e^{i\omega t}[/math]. Wymiar tej bazy powinien odpowiadać wymiarowi sygnału. Ponieważ dla każdej częstości zespolona transformata odtwarza amplitudę i fazę, to w widmie mocy będzie dwukrotnie mniej punktów niż w sygnale, dla którego liczono transformatę. Punkty w których liczymy transformatę Fouriera rozkładają się równomiernie od zera do częstości Nyquista, czyli połowy częstości próbkowania. Przy częstości próbkowania 128Hz częstość Nyquista wynosi 64Hz. Liczba punktów w transformacjie Fouriera wynosi tyle, ile w naturalne bazie sygnału, czyli 256. Połowa tych wartości opisuje amplitudy, a druga połowa fazy. Tak więc w widmie amplitudowym będzie 128 punktów, rozłożonych równomiernie od zera do 64 Hz, czyli rozdzielczość widma wyniesie w tym przypadku 0,5Hz.
Jako przykład 'z prawdziwego świata' spróbujmy rozszyfrować, skąd w przykładowym artykule[1] o interfejsach mózg-komputer opartych o SSVEP pojawiają się dziwne częstości 6,83 i 7,03 Hz.
Mamy tam do czynienia z 3-sekundowymi odcinkami sygnału próbkowanego z częstością 200Hz. Aby umożliwić stosowanie szybkiej transformaty Fouriera (FFT) oraz zwiększyć rozdzielczość, sygnał jest dopełniany (zerami) do 1024 punktów. Tak więc 512 punktów (1024/2) będzie w tym przypadku rozłożonych między 0 a 100 Hz, co daje odstęp 100/512, czyli ok. 0.195 Hz między kolejnymi częstościami. Punkty najbliższe 7Hz to 35*100/512 = 6,83 i 36*100/512 = 7,03 Hz.
- ↑ Xiaorong Gao, Dingfeng Xu, Ming Cheng and Shangkai Gao, "A BCI-based environmental controller for the motion-disabled" IEEE Transactions on Neural Systems and Rehabilitation Engineering, vol. 11, no. 2, pp. 137-140, June 2003, doi: 10.1109/TNSRE.2003.814449, https://web.archive.org/web/20091114205637id_/http://www.cis.gsu.edu/brainlab/papers/gao%202003%20-%2048N%20BCI.pdf