WnioskowanieStatystyczne/Interpretacja współczynnika korelacji: Różnice pomiędzy wersjami
| (Nie pokazano 11 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 9: | Linia 9: | ||
[[Plik:Wsp kor war.png|500px]] | [[Plik:Wsp kor war.png|500px]] | ||
| − | |||
<math> | <math> | ||
| Linia 22: | Linia 21: | ||
</math> | </math> | ||
| − | Całkowitą wariancję zmiennej <math>y</math> | + | |
| + | |||
| + | Całkowitą wariancję zmiennej <math>y</math> można podzielić na dwa | ||
człony: wariancję estymaty <math>y_{i}^{p}</math> wokół wartości | człony: wariancję estymaty <math>y_{i}^{p}</math> wokół wartości | ||
średniej <math>\overline{y}</math> i wariancję obserwowanych | średniej <math>\overline{y}</math> i wariancję obserwowanych | ||
<math>y_{i}</math> wokół estymaty <math>y_{i}^{p}</math> (trzeci człon | <math>y_{i}</math> wokół estymaty <math>y_{i}^{p}</math> (trzeci człon | ||
| − | [https://en.wikipedia.org/wiki/Explained_sum_of_squares#Simple_derivation znika]) | + | [https://en.wikipedia.org/wiki/Explained_sum_of_squares#Simple_derivation znika]): |
| + | |||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \underset{i=1}{\overset{N}{\sum }}(y_{i}-\overline{y})^{2}= | ||
| + | \underset{i=1}{\overset{N}{\sum }}(y_{i}-y_{i}^{p})^{2}+\underset{i=1}{ | ||
| + | \overset{N}{\sum }}(y_{i}^{p}-\overline{y})^{2} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | |||
| + | |||
===Współczynnik korelacji liniowej (Pearsona)=== | ===Współczynnik korelacji liniowej (Pearsona)=== | ||
| + | Rozważmy wariancję tłumaczoną przez model | ||
| + | <center> | ||
| + | :<math>\underset{i=1}{\overset{N}{\sum }}(y_{i}^{p}-\overline{y})^{2} </math> | ||
| + | </center> | ||
| − | + | Ponieważ <math>\forall_i (y_i^p - \overline{y}) = b (x_i^p - \overline{x} )</math>, | |
| + | :<math> | ||
| + | \underset{i=1}{\overset{N}{\sum }}(y_{i}^{p}-\overline{y})^{2} | ||
| + | = b^2 \underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x})^{2} | ||
| + | </math> | ||
| − | <math> | + | Jeśli prosta <math>y= a + b x</math> została dopasowana metodą największej wiarygodności, to <math> |
b=\frac{\underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x})(y_{i}- | b=\frac{\underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x})(y_{i}- | ||
| − | \overline{y})}{\underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x})^{2}}, | + | \overline{y})}{\underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x})^{2}} |
| − | \ | + | </math>, czyli |
| + | |||
| + | :<math> | ||
| + | \underset{i=1}{\overset{N}{\sum }}(y_{i}^{p}-\overline{y})^{2} | ||
| + | = b^2 \underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x})^{2} | ||
</math> | </math> | ||
| + | :<math> | ||
| + | \underset{i=1}{\overset{N}{\sum }}(y_{i}^{p}-\overline{y})^{2} | ||
| + | = b \underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x})^{2} | ||
| + | =\frac{\left( | ||
| + | \underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x})(y_{i}-\overline{y} | ||
| + | )\right) ^{2}}{\left( \underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x} | ||
| + | )^{2}\right) ^{2}}\underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x} | ||
| + | )^{2}=\\ | ||
| + | |||
| + | =\frac{\left( \underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x} | ||
| + | )(y_{i}-\overline{y})\right) ^{2}}{\underset{i=1}{\overset{N}{\sum }}(x_{i}- | ||
| + | \overline{x})^{2}}\frac{\underset{i=1}{\overset{N}{\sum }}(y_{i}-\overline{y} | ||
| + | )^{2}}{\underset{i=1}{\overset{N}{\sum }}(y_{i}-\overline{y})^{2}}=r^{2} | ||
| + | \underset{i=1}{\overset{N}{\sum }}(y_{i}-\overline{y})^{2} | ||
| + | </math> | ||
oraz wzór na estymator współczynnika korelacji liniowej | oraz wzór na estymator współczynnika korelacji liniowej | ||
| − | |||
<math> | <math> | ||
| Linia 48: | Linia 87: | ||
{\sqrt{E\left( (x-\mu_{x})^2\right) E\left( (y-\mu_{y})^2\right)}}, | {\sqrt{E\left( (x-\mu_{x})^2\right) E\left( (y-\mu_{y})^2\right)}}, | ||
</math> | </math> | ||
| − | |||
| − | |||
jego kwadrat estymujemy jako | jego kwadrat estymujemy jako | ||
| − | |||
| − | |||
<math> | <math> | ||
r^{2}=\frac{\left( \underset{i=1}{\overset{N}{\sum }}(x_{i}- | r^{2}=\frac{\left( \underset{i=1}{\overset{N}{\sum }}(x_{i}- | ||
| Linia 59: | Linia 94: | ||
\overline{y})^{2}} | \overline{y})^{2}} | ||
</math> | </math> | ||
| − | |||
Podstawiając | Podstawiając | ||
| Linia 70: | Linia 104: | ||
\overline{y})}{\underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x})^{2}} | \overline{y})}{\underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x})^{2}} | ||
</math> | </math> | ||
| − | |||
| − | |||
do wyrażenia na wariancję tłumaczoną przez model | do wyrażenia na wariancję tłumaczoną przez model | ||
| − | |||
:<math>\underset{i=1}{\overset{N}{\sum }}(y_{i}^{p}-\overline{y})^{2} </math>, | :<math>\underset{i=1}{\overset{N}{\sum }}(y_{i}^{p}-\overline{y})^{2} </math>, | ||
dostajemy: | dostajemy: | ||
| − | |||
| − | |||
:<math> | :<math> | ||
\underset{i=1}{\overset{N}{\sum }}(y_{i}^{p}-\overline{y})^{2} | \underset{i=1}{\overset{N}{\sum }}(y_{i}^{p}-\overline{y})^{2} | ||
| Linia 105: | Linia 134: | ||
</math> | </math> | ||
| − | |||
| − | |||
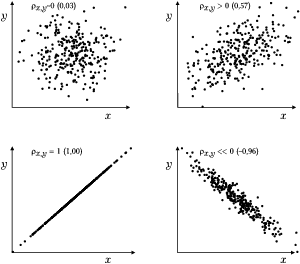
| − | [[Plik:Korelacja.png|600px|thumb| | + | [[Plik:Korelacja.png|600px|thumb|center|<figure id="fig:rozw2"></figure>Przykładowe wartości współczynnika korelacji dla 300 par <math>(x, y)</math> o |
różnych stopniach współzależności. | różnych stopniach współzależności. | ||
]] | ]] | ||
| + | |||
| + | |||
| + | Ciekawe przykłady korelacji liniowych dla zależności nieliniowych podaje [https://pl.wikipedia.org/wiki/Zale%C5%BCno%C5%9B%C4%87_zmiennych_losowych artykuł z Wikipedii] | ||
| + | |||
| + | ===Istotność statystyczna współczynnika korelacji=== | ||
| + | ...to osobny problem :-) | ||
Aktualna wersja na dzień 16:37, 6 maj 2025
Wnioskowanie_Statystyczne_-_wykład
Interpretacja współczynnika korelacji
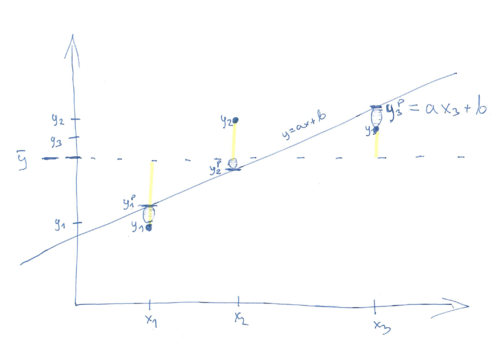
Rozważmy wariancję zmiennej [math]y[/math] z poprzedniego rozdziału. Niech [math]y_{i}^{p}=a+bx_{i}[/math]
[math] \underset{i=1}{\overset{N}{\sum }}(y_{i}-\overline{y})^{2}= \underset{i=1}{\overset{N}{\sum }}(y_{i}-y_{i}^{p}+y_{i}^{p}-\overline{y} )^{2}= [/math] [math] \underset{i=1}{\overset{N}{\sum }}(y_{i}-y_{i}^{p})^{2}+\underset{i=1}{ \overset{N}{\sum }}(y_{i}^{p}-\overline{y})^{2}+2\underset{i=1}{\overset{N}{ \sum }}(y_{i}-y_{i}^{p})(y_{i}^{p}-\overline{y}) [/math]
Całkowitą wariancję zmiennej [math]y[/math] można podzielić na dwa człony: wariancję estymaty [math]y_{i}^{p}[/math] wokół wartości średniej [math]\overline{y}[/math] i wariancję obserwowanych [math]y_{i}[/math] wokół estymaty [math]y_{i}^{p}[/math] (trzeci człon znika):
[math] \underset{i=1}{\overset{N}{\sum }}(y_{i}-\overline{y})^{2}= \underset{i=1}{\overset{N}{\sum }}(y_{i}-y_{i}^{p})^{2}+\underset{i=1}{ \overset{N}{\sum }}(y_{i}^{p}-\overline{y})^{2} [/math]
Współczynnik korelacji liniowej (Pearsona)
Rozważmy wariancję tłumaczoną przez model
- [math]\underset{i=1}{\overset{N}{\sum }}(y_{i}^{p}-\overline{y})^{2} [/math]
Ponieważ [math]\forall_i (y_i^p - \overline{y}) = b (x_i^p - \overline{x} )[/math],
- [math] \underset{i=1}{\overset{N}{\sum }}(y_{i}^{p}-\overline{y})^{2} = b^2 \underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x})^{2} [/math]
Jeśli prosta [math]y= a + b x[/math] została dopasowana metodą największej wiarygodności, to [math] b=\frac{\underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x})(y_{i}- \overline{y})}{\underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x})^{2}} [/math], czyli
- [math] \underset{i=1}{\overset{N}{\sum }}(y_{i}^{p}-\overline{y})^{2} = b^2 \underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x})^{2} [/math]
- [math] \underset{i=1}{\overset{N}{\sum }}(y_{i}^{p}-\overline{y})^{2} = b \underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x})^{2} =\frac{\left( \underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x})(y_{i}-\overline{y} )\right) ^{2}}{\left( \underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x} )^{2}\right) ^{2}}\underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x} )^{2}=\\ =\frac{\left( \underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x} )(y_{i}-\overline{y})\right) ^{2}}{\underset{i=1}{\overset{N}{\sum }}(x_{i}- \overline{x})^{2}}\frac{\underset{i=1}{\overset{N}{\sum }}(y_{i}-\overline{y} )^{2}}{\underset{i=1}{\overset{N}{\sum }}(y_{i}-\overline{y})^{2}}=r^{2} \underset{i=1}{\overset{N}{\sum }}(y_{i}-\overline{y})^{2} [/math]
oraz wzór na estymator współczynnika korelacji liniowej
[math] r_{x, y}= \frac{\sigma_{x, y}}{\sigma_x \sigma_y}= \frac{E\left( \left(x-\mu_{x})(y-\mu_{y}\right)\right)} {\sqrt{E\left( (x-\mu_{x})^2\right) E\left( (y-\mu_{y})^2\right)}}, [/math] jego kwadrat estymujemy jako [math] r^{2}=\frac{\left( \underset{i=1}{\overset{N}{\sum }}(x_{i}- \overline{x})(y_{i}-\overline{y})\right) ^{2}}{\underset{i=1}{\overset{N}{ \sum }}(x_{i}-\overline{x})^{2}\underset{i=1}{\overset{N}{\sum }}(y_{i}- \overline{y})^{2}} [/math]
Podstawiając [math] \forall_i (y_i - \overline{y}) = b (x_i - \overline{x} ) [/math], oraz [math] b=\frac{\underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x})(y_{i}- \overline{y})}{\underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x})^{2}} [/math] do wyrażenia na wariancję tłumaczoną przez model
- [math]\underset{i=1}{\overset{N}{\sum }}(y_{i}^{p}-\overline{y})^{2} [/math],
dostajemy:
- [math] \underset{i=1}{\overset{N}{\sum }}(y_{i}^{p}-\overline{y})^{2} = b \underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x})^{2} =\frac{\left( \underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x})(y_{i}-\overline{y} )\right) ^{2}}{\left( \underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x} )^{2}\right) ^{2}}\underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x} )^{2}=\\ =\frac{\left( \underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x} )(y_{i}-\overline{y})\right) ^{2}}{\underset{i=1}{\overset{N}{\sum }}(x_{i}- \overline{x})^{2}}\frac{\underset{i=1}{\overset{N}{\sum }}(y_{i}-\overline{y} )^{2}}{\underset{i=1}{\overset{N}{\sum }}(y_{i}-\overline{y})^{2}}=r^{2} \underset{i=1}{\overset{N}{\sum }}(y_{i}-\overline{y})^{2} [/math]
czyli
- [math] {r^{2}=\frac{\underset{i=1}{\overset{N}{\sum }}(y_{i}^{p}- \overline{y})^{2}}{\underset{i=1}{\overset{N}{\sum }}(y_{i}-\overline{y})^{2} }\ } [/math]
Ciekawe przykłady korelacji liniowych dla zależności nieliniowych podaje artykuł z Wikipedii
Istotność statystyczna współczynnika korelacji
...to osobny problem :-)
