STATLAB/Zadanie zaliczeniowe3: Różnice pomiędzy wersjami

Z Brain-wiki
m
 
(Nie pokazano 17 wersji utworzonych przez 2 użytkowników)
Linia 1: Linia 1:
−
===1. Przygotowanie danych===
+
[[ZasadyZaliczenia]]/Projekt_1
−
Nagraj przy użyciu mikrofonu kilka następujących po sobie dźwięków o różnej wysokości (np. cztery) zaśpiewanych lub zagranych na dowolnym instrumencie muzycznym. Dźwięk zapisz w formacie „raw”; zanotuj
 
−
częstotliwość próbkowania.
 
  
−
===2. Analiza czasowa widma===
+
<br>
−
Dla wybranego rodzaju okna czasowego i ustalonej szerokości okna <math>N_w \ll N</math>
+
<hr>
−
(<math>N</math> = długość sygnału), oblicz ''krótkoczasową transformatę Fouriera (STFT)'', czyli taką dwu-wymiarową tablicę (macierz numpy)
+
Projekt proszę przygotować w postaci '''notebooka''' z opisem poszczególnych kroków i własnych przemyśleń. Gotowy projekt prosimy przesyłać do Jarosława Żygierewicza (jarekz@fuw.edu.pl). W razie wątpliwości będziemy prosili o obronę projektu.
 +
<hr>
 +
===1. Dane ===
 +
Poniżej znajdują się linki do dwóch fragmentów utworów audio. Zapisane są w formacie wav. Pliki takie można wczytać do programu pythonowego za pomocą funkcji <tt>scipy.io.wavfile.read</tt>( [https://docs.scipy.org/doc/scipy-0.18.1/reference/generated/scipy.io.wavfile.read.html dokumentacja] tej funkcji.)
  
−
<math>
+
[https://drive.google.com/file/d/1bcving2rqJxtFwB6l40DqGKcxKYzg3Jr/view?usp=sharing Candy_Dulfer_-_Lily_Was_Here.wav]
−
Z[k][n_0] = \frac{\left\vert X_{n_0}[k] \right\vert^2}{N_w} \,,
 
−
</math>
 
  
−
że <math>X_{n_0}</math> jest dyskretną transformatą Fouriera okienkowanego wycinka sygnału od <math>n_0-\frac{N_w}{2}</math> o szerokości <math>N_w</math> (czyli wyśrodkowanego w <math>n_0</math>).
+
[https://drive.google.com/file/d/1CgOpkldAZnvd_zj1tGD572XLD3fDSIsJ/view?usp=sharing Rupert_Blaise_-_06_-_What_A_Wonderful_World.wav]
  
−
Proszę pamiętać o okienkowaniu ([[Nieparametryczne_widmo_mocy#Okienkowanie_a_widmo_mocy:_periodogram|periodogram]]) wycinka sygnału przed policzeniem DTF.
+
===2. Analiza czasowa widma: spektrogram===
 +
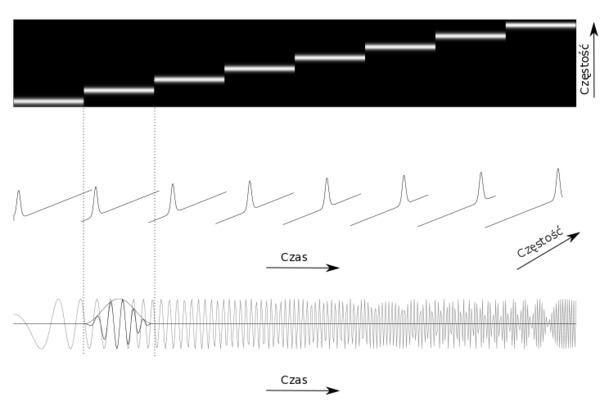
Programistyczna część projektu polega na samodzielnej  implementacji spektrogramu: reprezentacji rozkładu energii sygnału w dziedzinie czas-częstość. Idea tworzenia tej reprezentacji przedstawiona jest na poniższym rysunku.
 +
[[Plik:spectrogram.png|600px|thumb|center|Idea tworzenia spektrogramu]]
  
−
===3. Prezentacja===
 
−
Macierz wykreśl przy pomocy funkcji ''pylab.imshow'', podając zakresy poszczególnych osi przy użyciu parametru
 
  
−
<math>
+
Spektrogram otrzymujemy w następujący sposób:
−
\textrm{extent} = (t_{min}, t_{max}, f_{min}, f_{max}) \,.
+
* Sygnał dzielimy na fragmenty o długości '''N_okna'''
−
</math>
+
* Fragmenty mogą ale nie muszą na siebie nachodzić. Liczba próbek nachodzących niech będzie oznaczona '''N_wsp'''
 +
* Dla każdego fragmentu estymujemy widmo gęstości energii za pomocą ''periodogramu'' z okienkiem '''okno'''
 +
* Widma kolejnych fragmentów zapisujemy w macierzy numpy, tak, że i-ta kolumna zawiera widmo i-tego fragmentu
 +
* Macierz wykreśl przy pomocy funkcji <tt>pylab.imshow</tt>, podając zakresy poszczególnych osi przy użyciu parametru <tt>extent</tt>
  
−
===4. Interpretacja wyniku===
+
 
−
Powtórz punkty 2 i 3 dla kilku różnych szerokości okien <math>N_w</math> i zinterpretuj widoczne różnice.
+
Kod należy przygotować tak, aby łatwo było modyfikować:
 +
* '''okno''', '''N_okna''', '''N_wsp''',  czyli: typ okna, jego długość i stopień nachodzenia okien.
 +
* zakres czasu i częstości wyświetlanej reprezentacji: <math> t_{min}, t_{max}, f_{min}, f_{max}</math>
 +
* ważne jest też wyświetlenie właściwych skal czasu i częstości
 +
* wersja bardziej rozwinięta powinna także wyświetlać rozkłady brzegowe mocy tj.:
 +
** wzdłuż osi poziomej moc sygnału w czasie
 +
** wzdłuż osi pionowej widmo mocy z całego prezentowanego odcinka czasu
 +
wskazówka: można skorzystać z instrukcji w https://matplotlib.org/stable/tutorials/intermediate/arranging_axes.html; warto też zpoznać się z koncepcjami pracy z osiami i ich własnościami: https://matplotlib.org/stable/users/explain/axes/axes_intro.html
 +
 
 +
===3. Interpretacja wyniku===
 +
* Analizę spektrogramem wykonaj dla obu sygnałów i dla kilku różnych długości okien '''N_okna'''.  Zinterpretuj widoczne różnice.
 +
* Czy na podstawie takich spektrogramów jesteśmy w stanie odróżnić kiedy grał który instrument, lub kiedy był to głos ludzki?
 +
* Czy dałoby się w ten sposób określić tony podstawowe?
 +
 
 +
===4. Cochleogram: na bonus ===
 +
Zapoznać się z koncepcją cochleagramów (https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=7251910&tag=1) i porównać mapy czas częstość uzyskane tą techniką z mapami uzyskanymi za pomocą spektrogramów dla Rupert_Blaise_-_06_-_What_A_Wonderful_World.wav.
 +
 
 +
[[ZasadyZaliczenia]]/Projekt_1

Aktualna wersja na dzień 09:06, 13 gru 2023

ZasadyZaliczenia/Projekt_1


Projekt proszę przygotować w postaci notebooka z opisem poszczególnych kroków i własnych przemyśleń. Gotowy projekt prosimy przesyłać do Jarosława Żygierewicza (jarekz@fuw.edu.pl). W razie wątpliwości będziemy prosili o obronę projektu.

1. Dane

Poniżej znajdują się linki do dwóch fragmentów utworów audio. Zapisane są w formacie wav. Pliki takie można wczytać do programu pythonowego za pomocą funkcji scipy.io.wavfile.read( dokumentacja tej funkcji.)

Candy_Dulfer_-_Lily_Was_Here.wav

Rupert_Blaise_-_06_-_What_A_Wonderful_World.wav

2. Analiza czasowa widma: spektrogram

Programistyczna część projektu polega na samodzielnej implementacji spektrogramu: reprezentacji rozkładu energii sygnału w dziedzinie czas-częstość. Idea tworzenia tej reprezentacji przedstawiona jest na poniższym rysunku.

Idea tworzenia spektrogramu


Spektrogram otrzymujemy w następujący sposób:

  • Sygnał dzielimy na fragmenty o długości N_okna
  • Fragmenty mogą ale nie muszą na siebie nachodzić. Liczba próbek nachodzących niech będzie oznaczona N_wsp
  • Dla każdego fragmentu estymujemy widmo gęstości energii za pomocą periodogramu z okienkiem okno
  • Widma kolejnych fragmentów zapisujemy w macierzy numpy, tak, że i-ta kolumna zawiera widmo i-tego fragmentu
  • Macierz wykreśl przy pomocy funkcji pylab.imshow, podając zakresy poszczególnych osi przy użyciu parametru extent


Kod należy przygotować tak, aby łatwo było modyfikować:

  • okno, N_okna, N_wsp, czyli: typ okna, jego długość i stopień nachodzenia okien.
  • zakres czasu i częstości wyświetlanej reprezentacji: [math] t_{min}, t_{max}, f_{min}, f_{max}[/math]
  • ważne jest też wyświetlenie właściwych skal czasu i częstości
  • wersja bardziej rozwinięta powinna także wyświetlać rozkłady brzegowe mocy tj.:
    • wzdłuż osi poziomej moc sygnału w czasie
    • wzdłuż osi pionowej widmo mocy z całego prezentowanego odcinka czasu

wskazówka: można skorzystać z instrukcji w https://matplotlib.org/stable/tutorials/intermediate/arranging_axes.html; warto też zpoznać się z koncepcjami pracy z osiami i ich własnościami: https://matplotlib.org/stable/users/explain/axes/axes_intro.html

3. Interpretacja wyniku

  • Analizę spektrogramem wykonaj dla obu sygnałów i dla kilku różnych długości okien N_okna. Zinterpretuj widoczne różnice.
  • Czy na podstawie takich spektrogramów jesteśmy w stanie odróżnić kiedy grał który instrument, lub kiedy był to głos ludzki?
  • Czy dałoby się w ten sposób określić tony podstawowe?

4. Cochleogram: na bonus

Zapoznać się z koncepcją cochleagramów (https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=7251910&tag=1) i porównać mapy czas częstość uzyskane tą techniką z mapami uzyskanymi za pomocą spektrogramów dla Rupert_Blaise_-_06_-_What_A_Wonderful_World.wav.

ZasadyZaliczenia/Projekt_1

Źródło: „http://brain.fuw.edu.pl/edu/index.php?title=STATLAB/Zadanie_zaliczeniowe3&oldid=9696”