Wstep: Różnice pomiędzy wersjami
| Linia 9: | Linia 9: | ||
Żeby odtworzyć fizyczne własności sygnału, czyli narysować zapisane wartości próbek (czarne kropki) w odpowiedniej skali, musimy znać ''częstość próbkowania'' i ''stałą kalibracji''. | Żeby odtworzyć fizyczne własności sygnału, czyli narysować zapisane wartości próbek (czarne kropki) w odpowiedniej skali, musimy znać ''częstość próbkowania'' i ''stałą kalibracji''. | ||
| − | Wyrażana w hercach (Hz) częstość próbkowania <math> | + | Wyrażana w hercach (Hz) częstość próbkowania (ang. ''sampling frequency'', <math>f_s</math>) to liczba próbek na sekundę. Jest ona odwrotnością odstępu w czasie między kolejnymi próbkami (<math>\Delta t</math>): |
<div align = "center> | <div align = "center> | ||
| − | <math> | + | <math>f_s = \dfrac{1}{\Delta t}</math> |
</div> | </div> | ||
| Linia 21: | Linia 21: | ||
Poza znajomością zależności między zapisanymi liczbami a jednostkami fizycznymi w procesie próbkowania kluczową rolę odgrywa twierdzenie o próbkowaniu (inaczej twierdzenie Nyquista-Shannona, czasem w skrócie twierdzenie Nyquista). Mówi ono, że sygnał ciągły możemy odtworzyć za zapisanych próbek, jeśli częstość próbkowania <math>f_p</math> była wyższa niż dwukrotność najwyższej z występujących w sygnale częstości <math>f_{max}</math>, nazywana częstością Nyquista <math>f_N</math>: | Poza znajomością zależności między zapisanymi liczbami a jednostkami fizycznymi w procesie próbkowania kluczową rolę odgrywa twierdzenie o próbkowaniu (inaczej twierdzenie Nyquista-Shannona, czasem w skrócie twierdzenie Nyquista). Mówi ono, że sygnał ciągły możemy odtworzyć za zapisanych próbek, jeśli częstość próbkowania <math>f_p</math> była wyższa niż dwukrotność najwyższej z występujących w sygnale częstości <math>f_{max}</math>, nazywana częstością Nyquista <math>f_N</math>: | ||
<div align = "center> | <div align = "center> | ||
| − | <math> | + | <math> f_s = \dfrac{1}{\Delta t} > 2* f_{max} = f_N</math> |
</div> | </div> | ||
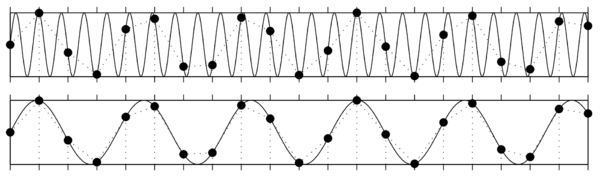
Jeśli częstość próbkowania nie byłą wystarczająco wysoka, nie tylko stracimy informację o zmianach amplitudy sygnału "pomiędzy próbkami", ale dojdzie też do zafałszowania sygnału w niższych częstościach, które z pozoru nie powinny być zaburzone. Efekt ten jest omówiony w rozdziale [[Aliasing]]. | Jeśli częstość próbkowania nie byłą wystarczająco wysoka, nie tylko stracimy informację o zmianach amplitudy sygnału "pomiędzy próbkami", ale dojdzie też do zafałszowania sygnału w niższych częstościach, które z pozoru nie powinny być zaburzone. Efekt ten jest omówiony w rozdziale [[Aliasing]]. | ||
Wersja z 19:24, 25 lip 2024
Sygnały zapisujemy, przetwarzamy i analizujemy w postaci ciągów liczb. Przejście od sygnału ciągłego do cyfrowego odbywa się przez proces próbkowania, czyli zapisywania kolejnych amplitud sygnału w ustalonych, stałych odstępach czasu, omawiany wcześniej na TIiK.
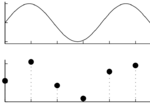
Ciągły sygnał z górnego rysunku, po próbkowaniu w punktach symbolizowanych czarnymi kropkami na rysunku dolnym, na dysku zostaje zapisany jako ciąg liczb:
102, 195, 80, 16, 147, 178
Żeby odtworzyć fizyczne własności sygnału, czyli narysować zapisane wartości próbek (czarne kropki) w odpowiedniej skali, musimy znać częstość próbkowania i stałą kalibracji.
Wyrażana w hercach (Hz) częstość próbkowania (ang. sampling frequency, [math]f_s[/math]) to liczba próbek na sekundę. Jest ona odwrotnością odstępu w czasie między kolejnymi próbkami ([math]\Delta t[/math]):
[math]f_s = \dfrac{1}{\Delta t}[/math]
Stała kalibracji to współczynnik, przez który mnożymy zapisane liczby, żeby otrzymać wartości w jednostkach fizycznych, na przykład mikrowoltach.
Oczywiście musimy też wiedzieć, w jakim formacie zapisano na dysku liczby (to omawialiśmy na wykładzie o binarnych reprezentacjach liczb, oraz, w przypadku sygnałów wielozmiennych o jednolitym próbkowaniu, znać liczbę kanałów. Taka dodatkowa informacja (metainformacja) jest konieczna do poprawnego wyświetlenia danych z pliku.
Aliasing
Poza znajomością zależności między zapisanymi liczbami a jednostkami fizycznymi w procesie próbkowania kluczową rolę odgrywa twierdzenie o próbkowaniu (inaczej twierdzenie Nyquista-Shannona, czasem w skrócie twierdzenie Nyquista). Mówi ono, że sygnał ciągły możemy odtworzyć za zapisanych próbek, jeśli częstość próbkowania [math]f_p[/math] była wyższa niż dwukrotność najwyższej z występujących w sygnale częstości [math]f_{max}[/math], nazywana częstością Nyquista [math]f_N[/math]:
[math] f_s = \dfrac{1}{\Delta t} \gt 2* f_{max} = f_N[/math]
Jeśli częstość próbkowania nie byłą wystarczająco wysoka, nie tylko stracimy informację o zmianach amplitudy sygnału "pomiędzy próbkami", ale dojdzie też do zafałszowania sygnału w niższych częstościach, które z pozoru nie powinny być zaburzone. Efekt ten jest omówiony w rozdziale Aliasing.
Celem pierwszego wykładu jest wprowadzenie pojęć, potrzebnych na pierwszych ćwiczeniach:
- częstość próbkowania
- częstość Nyquista
- aliasing
- sygnał dyskretny jako wektor
- szereg Fouriera
- transformata Fouriera