Aliasing
Spis treści
AS/ Przekształcenie Fouriera sygnałów dyskretnych, aliasing
Próbkowanie odwrotnej transformaty Fouriera
Przypomnijmy wzór na odwrotną transformację Fouriera sygnału ciągłego [math] s(t)=\int_{-\infty}^{\infty}\hat{s}(f)e^{-i 2\pi t f} d f [/math]
Dyskretne wartości tego sygnału, próbkowane w chwilach [math]n \Delta t[/math], możemy odtworzyć z powyższgo równania dla [math]t = n \Delta t[/math]
[math] \sum_{r=-\infty}^\infty \int_\frac{(2r - 1)}{2\Delta t}^\frac{(2r + 1) }{2\Delta t} \hat{s}(f)e^{-i 2\pi n \Delta t f} d f \;\; \stackrel{f \rightarrow f+\frac{r}{\Delta t}}{=} \;\; [/math] [math] \sum_{r=-\infty}^\infty \int_\frac{-1}{2\Delta t}^\frac{1}{2\Delta t} \hat{s}\left(f + \frac{r}{\Delta t}\right)e^{-i 2\pi n \Delta t (f + \frac{r}{\Delta t})} d f [/math]
[math] = \int_\frac{-1}{2\Delta t}^\frac{1}{2\Delta t} \sum_{r=-\infty}^\infty \hat{s}\left(f + \frac{r}{\Delta t}\right)e^{-i 2\pi n \Delta t f} d f [/math]Szukając wartości sygnału w dyskretnych chwilach czasu, dostaliśmy w miejsce odwrotnej transformaty Fouriera całkę w ograniczonym zakresie z funkcji będącej (nieskończoną) sumą powtórzeń transformaty Fouriera sygnału ciągłego, przesuwanej o wielokrotności odwrotności [math]\Delta t[/math].
Splot z grzebieniem Diraca
Innym sposobem pokazania powyższego efektu jest przedstawienie sekwencji dyskretnej [math]s[n][/math] jako iloczynu sygnału ciągłego [math]s(t)[/math] z grzebieniem Diraca
[math] D(t) = \sum_{k=-\infty}^{\infty} \delta(t-k\Delta t) [/math]
Policzmy transformatę Fouriera grzebienia Diraca [math]\hat{D}(t)[/math]:
[math] \hat{D}(f) = \mathcal{F}(D(t)) = \mathcal{F}\left(\sum_{k=-\infty}^{\infty} \delta(t-k\Delta t) \right) = \int_{-\infty}^{\infty} \sum_{k=-\infty}^{\infty} \delta(t-k\Delta t) e^{i 2\pi f t} dt = [/math] [math] \sum_{k=-\infty}^{\infty} \int_{-\infty}^{\infty} \delta(t-k\Delta t) e^{i 2\pi f t} dt = \sum_{k=-\infty}^{\infty} e^{i 2\pi f k\Delta t} [/math]
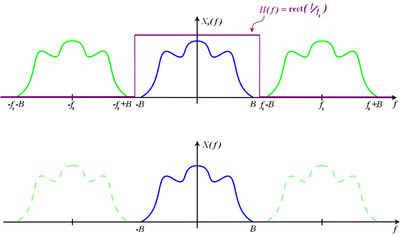
Zgodnie z twierdzeniem o splocie, iloczyn sygnału z grzebieniem Diraca w przestrzeni czasu będzie odpowiadał w dziedzinie częstości, splotowi transformaty Fouriers sygnału [math]\hat{s}(t)[/math] z wyliczoną powyżej transformatę Fouriera grzebienia Diraca, będącą jak widać grzebieniem Diraca w przestrzeni częstości.
Przypomnijmy (np. z rozważań o systemach liniowych niezmienniczych w czasie), że splot z deltą Diraca w zerze jest identycznością, a splot z [math]\delta(t-kT)[/math] przesuwa funkcję o [math]kT[/math]. Z liniowości splotu dostajemy sumę powtórzeń transformaty Fouriera sygnału ciągłego, przesuwanej o wielokrotności odwrotności [math]\Delta t[/math].
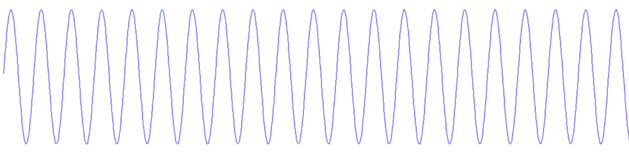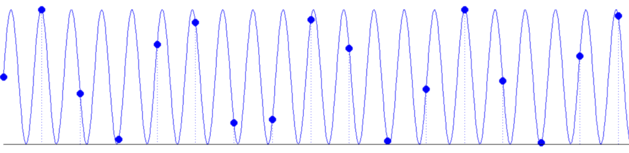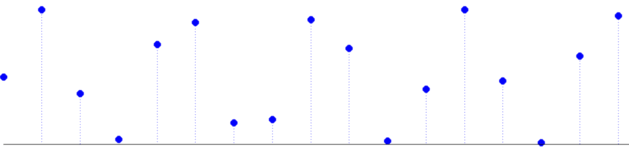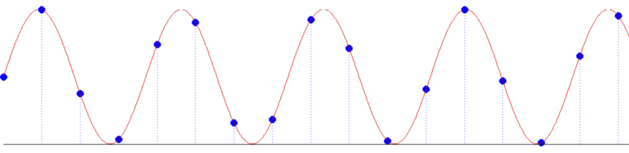
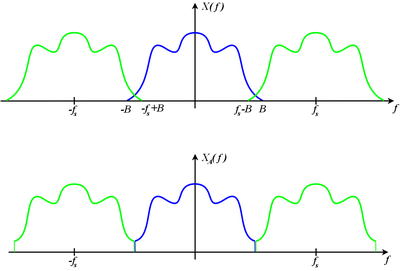
Poniższe rysunki z [Wikipedii] ilustrują ten efekt dla przypadku próbkowania z częstością większą i mniejszą od częstości Nyquista:
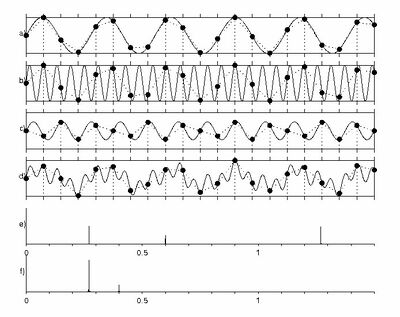
Kolejny przykład ilustruje aliasing w dziedzinie czasu:
AS/ Twierdzenie o próbkowaniu
Twierdzenie o próbkowaniu odpowiada na kluczowe pytanie, które winniśmy postawić decydując się na pracę z dyskretnymi (próbkowanymi) wersjami sygnałów ciągłych z natury.
Twierdzenie o próbkowaniu
Sygnał ciągły [math]s(t)[/math] możemy odtworzyć z wektora jego wartości w dyskretnych chwilach czasu [math] n \Delta t[/math], jeśli nie było w nim częstości wyższych niż [math]\frac{1}{2\, \Delta t}[/math].
Dowód
Dla uproszczenia przyjmijmy [math]\Delta t = 1[/math]. Wtedy [math]\hat{s}(f)[/math], czyli transformata Fouriera sygnału [math]s(t)[/math], będzie niezerowa co najwyżej pomiędzy [math]-\frac{1}{2}[/math] a [math]\frac{1}{2}[/math].
Oznaczmy [math]u(f)[/math] funkcję o okresie [math]1[/math], tożsamą z [math]\hat{s}(f)[/math] na przedziale [math] \left [ -\frac{1}{2}, \frac{1}{2} \right ] [/math].
Przedstawia ją szereg Fouriera:
[math]u(f) = \sum_{n=-\infty}^{+\infty} c_n e^{-2 \pi i f n}[/math]
Współczynniki [math] c_n [/math] tego rozwinięcia dane są wzorem:
[math] c_{n} =\frac{1}{1} \int_{0}^{1} u(f) e^{{2\pi i n f}} d f = \int_{- \frac{1}{2}}^{\frac{1}{2}} \hat{s}(f)e^{{2\pi i n f}} d f = \int_{-\infty}^{\infty} \hat{s}(f) e^{{2\pi i n f}} d f = s(n) [/math]
Współczynniki [math]c_n[/math], dane przez wartości sygnału [math]s[/math] w punktach próbkowania, jednoznacznie określają funkcję [math]u(f)[/math], ta z kolei zawiera w sobie [math]\hat{s}(f)[/math] — transformatę Fouriera ciągłego sygnału [math]s(t)[/math], czyli określa jednoznacznie również sam sygnał.
Znajdźmy explicite formułę rekonstrukcji:
[math] s(t) = \int_{-\infty}^{\infty} \hat{s}(f) e^{-2\pi i f t } d f = \int_{- \frac{1}{2}}^{\frac{1}{2}} \hat{s}(f) e^{-2\pi i f t } d f = \int_{- \frac{1}{2}}^{\frac{1}{2}} \left ( \sum_{n=-\infty}^{+\infty} c_n e^{-2\pi i f n} \right )e^{-2\pi i f t} df [/math] [math] = \sum_{n=-\infty}^{+\infty} \int_{-\frac{1}{2}}^{\frac{1}{2}} s(n) e^{2 \pi i f n} e^{-2\pi i f t} df = \sum_{n=-\infty}^{+\infty} s(n) \int_{-\frac{1}{2}}^{\frac{1}{2}} e^{2 \pi i f (n-t)} df [/math]
ponieważ
[math] \int_{-\frac{1}{2}}^{\frac{1}{2}} e^{2 \pi i f (n-t)} df = \left[{\frac{1}{2\pi i (n-t)}} e^{2 \pi i f (n-t)} \right]_{f=-\frac{1}{2}}^{f=\frac{1}{2}} =\frac{\sin\left( \pi (n-t)\right)}{\pi(n-t)} [/math]
dostajemy
[math] s(t)=\sum_{n=-\infty}^{+\infty} { {s(n)} } \frac{\sin\left(\pi (n-t)\right)}{\pi(n-t)} [/math]
Tak więc, jeśli spełnione jest główne założenie o ograniczonym paśmie sygnału ciągłego i odpowiednio dobranej częstości próbkowania, w procesie próbkowania nie tracimy informacji ani też nie wprowadzamy przekłamań, obliczając widmo (rozdział o aliasingu).
Twierdzenie o próbkowaniu w praktyce
W praktyce przed próbkowaniem sygnał jest zwykle filtrowany dolnoprzepustowym filtrem analogowym o częstości odcięcia poniżej częstości Nyquista.