WnioskowanieStatystyczne/CLT

Wnioskowanie_Statystyczne_-_wykład

Centralne Twierdzenie Graniczne

Rozkład Gaussa pełni w statystyce bardzo znaczącą rolę ze względu na Centralne Twierdzenie Graniczne , według którego rozkład sumy dużej liczby zmiennych losowych o podobnych wielkościach dąży (przy liczbie sumowanych zmiennych dążących do nieskończoności) do rozkładu Gaussa. Poniżej przytoczymy dowód tego twierdzenia dla uproszczonego przypadku sumy zmiennych pochodzących z tego samego rozkładu.

Twierdzenie Lindeberga — Levy'ego

Zakładamy, że [math]x_{i}[/math] są niezależnymi zmiennymi podlegającymi (dowolnemu) rozkładowi o skończonej wartości oczekiwanej [math]\mu[/math] i wariancji [math]\sigma ^{2}[/math]. Dla [math]n\rightarrow \infty[/math], wielkość

[math] y=\frac{ \left(\sum\limits_{i=1}^{n} x_{i}\right) -n\mu }{\sigma \sqrt{n}} [/math]

podlega rozkładowi normalnemu o wartości średniej 0 i wariancji 1.

Dowód

W dowodzie skorzystamy z pojęcia funkcji tworzącej (charakterystycznej) rozkładu. Dla zmiennej losowej [math]x[/math] jest to wartość oczekiwana wyrażenia [math]e^{itx}[/math], gdzie [math]i=\sqrt{-1}[/math]. Dla rozkładów ciągłych jest to transformata Fouriera funkcji gęstości prawdopodobieństwa [math]f(x)[/math]:

[math] \phi_x (t)=E(e^{itx})=\underset{-\infty }{\overset{\infty }{\int }} e^{itx}f\left( x\right) dx [/math]

Użyteczne będą następujące związki, które wyprowadzić można bezpośrednio z powyższej definicji:

funkcja tworząca sumy zmiennych niezależnych

Dla niezależnych zmiennych [math]x[/math] i [math]y[/math]:

[math] w=x+y\Rightarrow \phi _{w}(t) =\phi _{x}\left( t\right) \cdot \phi_{y}(t). [/math]

Dowód:

[math] \phi _{w}(t) = E(e^{it(x+y)})=E(e^{itx}\cdot e^{ity}) = E(e^{itx})\cdot E(e^{ity})=\phi _{x}\left( t\right) \cdot \phi_{y}(t). [/math]

pochodna funkcji tworzącej

Bezpośrednio z definicji (różniczkujemy po [math]dt[/math], więc przy każdym różniczkowaniu spada nam z wykładnika [math]i x[/math], [math]x[/math] zostaje pod całką a [math]i[/math] jako stała wychodzi przed całkę) widać, że:

[math] \frac{d^{n}\phi (t)}{dt^{n}}=i^{n}\underset{}{\underset{-\infty }{\overset{ \infty }{\int }}x^{n}}\ e^{itx}f(x) dx [/math]

związek pochodnej funkcji tworzącej z momentami zmiennej losowej

[math]n[/math]-ta pochodna funkcji tworzącej w zerze (czyli dla [math]t=0[/math]) wynosi

[math] \phi^{(n)}(0)= i^{n}\underset{}{\underset{-\infty }{\overset{\infty }{\int }}x^{n}}\ e^{i 0 x} f(x) dx = i^{n}\underset{}{\underset{-\infty }{\overset{\infty }{\int }}x^{n}} f(x) dx = i^{n}E(x^{n}) [/math]

transformata Fouriera funkcji Gaussa

Funkcja tworząca rozkładu normalnego o wartości oczekiwanej 0 i jednostkowej wariancji będzie miała postać

[math] \phi _{x}(t)= \int\limits_{-\infty}^\infty e^{itx}\frac{e^{\frac{-x^{2}}{2}}}{\sqrt{2\pi }}dx= (\dots)=e^{\frac{-t^{2}}{2}}. [/math]

W analizie sygnałów wynik ten będzie oznaczał, że tranformata Fouriera funkcji Gaussa jest również funkcją Gaussa. Do wyliczeń zastąpionych powyżej przez (...) możemy np. skorzystać z tablicy całek oznaczonych, w których znajdujemy wzór [math]\int\limits_{-\infty}^\infty e^{-a x^2 + 2 b x} dx = \sqrt{\frac{\pi}{a}} e^{-\frac{b^2}{a}}[/math] dla [math]a\gt 0[/math].

Wróćmy do dowodu --- interesuje nas suma zmiennych [math]x_i[/math] o wartości oczekiwanej [math]\mu[/math] i wariancji [math]\sigma^2[/math]. Funkcję tworzącą dla jednej zmiennej [math]x_i[/math] możemy rozwinąć w szereg Taylora

[math] \phi(z)=\underset{n=0}{\overset{\infty }{\sum }}\frac{\phi^{(n)}(z_{0})}{n!} (z-z_{0})^{n} [/math]

wokół [math]z_0[/math]. Rozpatrzmy zmienną [math]y_i[/math] przesuniętą względem [math]x_i[/math] o [math]-\mu[/math] i przeskalowaną czynnikiem [math]\sigma\sqrt{n}[/math]:

[math] y_{i}=\frac{x_{i}-\mu}{\sigma \sqrt{n}}. [/math]

Wtedy z (4) wynika, że [math]\phi^{(0)}(0)=1[/math], [math]\phi^{(1)}(0)=0[/math], a [math]\phi^{(2)}(0)=-\frac1 n[/math], czyli funkcja tworząca [math]y_i[/math] rozwinięta w szereg Taylora (5) będzie miała postać

[math] \phi_{y_i}(t)=1-\frac{t^{2}}{2n}+\cdots . [/math]

Korzystając ze wzoru (2) możemy przedstawić pierwsze wyrazy rozwinięcia Taylora sumy [math]y=\sum_{i=1}^n y_i[/math], odpowiadającej transformacji (1) z dowodzonego twierdzenia, jako iloczyn [math]n[/math] funkcji tworzących (6):

[math] \phi_y(t)=\left(1-\frac{t^2}{2n}+\ldots\right)^n. [/math]

Przy przejściu z [math]n[/math] do nieskończoności (i konsekwentnym pomijaniu wyrazów rzędu [math]n^{-2}[/math]) dostajemy

[math] \phi_y(t)\rightarrow \underset{n\rightarrow \infty }{\lim }\left(1-\frac{t^2}{2n}\right)^n= e^{\frac{-t^{2}}{2}} [/math]

czyli funkcję tworzącą rozkładu normalnego.

Ilustracja działania Centralnego Twierdzenia Granicznego. Zmienną [math]x_i[/math] bierzemy z rozkładu równomiernego, kolejne histogramy przedstawiają sumę 2, 3 i 4 zmiennych [math]x_i[/math] dla \mbox{10 000} losowań. Widać dużą zgodność z dopasowanym rozkładem normalnym (ciągła linia) już dla niewielu sumowanych zmiennych.

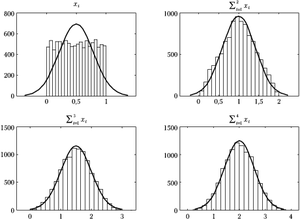
Rysunek 1 ilustruje powyższe twierdzenie dla przypadku sumy zmiennych pochodzących z rozkładu równomiernego. Jak widać, już dla sumy 3 zmiennych rozkład wydaje się bardzo podobny do normalnego. Niestety, często istotne bywają różnice w ,,ogonach, czyli dla wartości bardzo dużych lub bardzo małych. Otóż według wzoru wartości gęstości prawdopodobieństwa rozkładu normalnego dążą do zera dla dużych wartości bezwzględnych zmiennej asymptotycznie, lecz zera faktycznie nie osiągają. Inaczej mówiąc, prawdopodobieństwo wylosowania dowolnie dużej wartości z rozkładu Gaussa będzie małe, ale nie zerowe. Za to suma np. czterech zmiennych z rozkładu równomiernego od zera do jedynki (prawy dolny wykres rys. 1) nie przekroczy nigdy wartości 4, czyli prawdopodobieństwo dla [math]x\gt 4[/math] będzie dokładnie zerem. I choć w skali rysunku 1 efekt ten jest prawie niewidoczny, warto pamiętać, że testy oparte na założeniu normalności rozkładów często operują właśnie w okolicach tych "ogonów", gdzie przybliżenie rozkładu normalnego, uzyskane za pomocą tej prostej procedury, zawodzi.

---