
WnioskowanieStatystyczne/Bonferroni: Różnice pomiędzy wersjami
| Linia 31: | Linia 31: | ||
==Wielokrotne porównania== | ==Wielokrotne porównania== | ||
| + | Problem wielokrotnych porównań (ang. multiple comparisons) pojawia się w eksploracyjnej (w odróżnieniu od konfirmacyjnej) analizie danych, por. np. http://en.wikipedia.org/wiki/Data_dredging zwane też ''p''-hacking. | ||
| + | |||
| + | ===Przykład=== | ||
<math>N</math> obserwacji podzielonych na 7 grup. Testujemy hipotezę, że średnie tych grup są równe -- czyli niejako przyporządkowanie do grup jest przypadkowe. | <math>N</math> obserwacji podzielonych na 7 grup. Testujemy hipotezę, że średnie tych grup są równe -- czyli niejako przyporządkowanie do grup jest przypadkowe. | ||
| − | Możemy wykonać <math>\binom{7}{2}=21</math> testów różnic między grupami. Jeśli przyjmiemy poziom istotności 0.05, mamy dużą szansę na dokonanie fałszywego odkrycia. | + | Możemy wykonać <math>\binom{7}{2}=21</math> testów różnic między grupami. Jeśli przyjmiemy poziom istotności <math>\alpha=0.05</math>, mamy dużą szansę na dokonanie fałszywego odkrycia. Jak dużą? |
| + | |||
| + | ===FWER: family-wise error rate=== | ||
| + | Poziom istotności zdefiniowany dla pojedynczych testów zastępujemy pojęciem FWER, czyli prawdopodobieństwem popełnienia przynajmniej jednego błędu I rodzaju w grupie (rodzinie) testów. | ||
| + | |||
| + | ===Poprawka Bonferroniego=== | ||
| + | gwarantuje, że jeśli każdy z <math>m</math> testów wykonamy na poziomie istotności <math>\frac{\alpha}{m}</math>, to <math>\mathrm{FWER}=\alpha</math>. | ||
| − | + | Rozważmy rodzinę <math>m</math> testów (w powyższym przykładzie <math>m=21</math>), przypisując każdemu z nich p-wartość (ang. p-value) <math>p_i</math>. FWER, czyli prawdopodobieństwo popełnienia przynajmniej jednego błędu I rodzaju w tej rodzinie <math>m</math> testów, będzie nie większe niż suma prawdopodobieństw popełnienia błędu I rodzaju w każdym testów z osobna | |
| − | + | <math> P\left(p_i\leq\frac \alpha m\right)</math> | |
| + | niezależnie od tego, czy testy są niezależne czy nie | ||
| − | + | <math> \text{FWER} \leq\sum_{i=1}^{m}\left\{P\left(p_i\leq\frac \alpha m\right)\right\} | |
| + | \leq m \frac{\alpha}{m} = \alpha.</math> | ||
| + | Nierówność jest słuszna również w przypadku, kiedy tylko część z <math>m</math> hipotez jest prawdziwa. Jak widać jest to poprtawka bardzo konserwatywna, wymuszająca przeprowadzanie testów na potencjalnie zaniżonych poziomach istotności <math>\frac{\alpha}{m}</math>. | ||
==Evaluation of measurement data — Guide to the expression of uncertainty in measurement== | ==Evaluation of measurement data — Guide to the expression of uncertainty in measurement== | ||
Wersja z 18:21, 4 maj 2017
Spis treści
Błędy I i II rodzaju
Przyjęcie poziomu istotności ([math]\alpha[/math]) na poziomie 5 procent oznacza, że średnio w jednym na dwadzieścia przypadków możemy odrzucić prawdziwą hipotezę, czyli popełnić błąd I rodzaju (false positive).
Dla kompletności przypomnijmy, że błąd II rodzaju polega na przyjęciu hipotezy fałszywej (false negative) i jest związany z poziomem istotności testu.
Pojęcia błędów I i II rodzaju, podobnie jak hipotezy zerowej (H0) wprowadzili do statystyki Jerzy Spława-Neyman i Egon Pearson w latach 30. XX wieku.
| hipoteza H0 | |||
| Prawdziwa | Fałszywa | ||
|---|---|---|---|
| decyzja | Odrzuć | błąd typu I (False Positive) | poprawna (True Positive) |
| Przyjmij | poprawna (True Negative) | błąd typu II (False Negative) | |
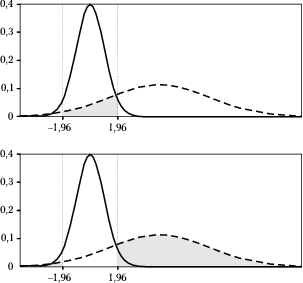
Wielokrotne porównania
Problem wielokrotnych porównań (ang. multiple comparisons) pojawia się w eksploracyjnej (w odróżnieniu od konfirmacyjnej) analizie danych, por. np. http://en.wikipedia.org/wiki/Data_dredging zwane też p-hacking.
Przykład
[math]N[/math] obserwacji podzielonych na 7 grup. Testujemy hipotezę, że średnie tych grup są równe -- czyli niejako przyporządkowanie do grup jest przypadkowe. Możemy wykonać [math]\binom{7}{2}=21[/math] testów różnic między grupami. Jeśli przyjmiemy poziom istotności [math]\alpha=0.05[/math], mamy dużą szansę na dokonanie fałszywego odkrycia. Jak dużą?
FWER: family-wise error rate
Poziom istotności zdefiniowany dla pojedynczych testów zastępujemy pojęciem FWER, czyli prawdopodobieństwem popełnienia przynajmniej jednego błędu I rodzaju w grupie (rodzinie) testów.
Poprawka Bonferroniego
gwarantuje, że jeśli każdy z [math]m[/math] testów wykonamy na poziomie istotności [math]\frac{\alpha}{m}[/math], to [math]\mathrm{FWER}=\alpha[/math].
Rozważmy rodzinę [math]m[/math] testów (w powyższym przykładzie [math]m=21[/math]), przypisując każdemu z nich p-wartość (ang. p-value) [math]p_i[/math]. FWER, czyli prawdopodobieństwo popełnienia przynajmniej jednego błędu I rodzaju w tej rodzinie [math]m[/math] testów, będzie nie większe niż suma prawdopodobieństw popełnienia błędu I rodzaju w każdym testów z osobna
[math] P\left(p_i\leq\frac \alpha m\right)[/math]
niezależnie od tego, czy testy są niezależne czy nie
[math] \text{FWER} \leq\sum_{i=1}^{m}\left\{P\left(p_i\leq\frac \alpha m\right)\right\} \leq m \frac{\alpha}{m} = \alpha.[/math]
Nierówność jest słuszna również w przypadku, kiedy tylko część z [math]m[/math] hipotez jest prawdziwa. Jak widać jest to poprtawka bardzo konserwatywna, wymuszająca przeprowadzanie testów na potencjalnie zaniżonych poziomach istotności [math]\frac{\alpha}{m}[/math].
Evaluation of measurement data — Guide to the expression of uncertainty in measurement
JCGM 100:2008 GUM 1995 with minor corrections http://www.iso.org/sites/JCGM/GUM-JCGM100.htm
3.4.8 Although this Guide provides a framework for assessing uncertainty, it cannot substitute for critical thinking, intellectual honesty and professional skill. The evaluation of uncertainty is neither a routine task nor a purely mathematical one; it depends on detailed knowledge of the nature of the measurand and of the measurement. The quality and utility of the uncertainty quoted for the result of a measurement therefore ultimately depend on the understanding, critical analysis, and integrity of those who contribute to the assignment of its value.