WnioskowanieStatystyczne/Interpretacja współczynnika korelacji: Różnice pomiędzy wersjami
| Linia 42: | Linia 42: | ||
<math> | <math> | ||
| − | + | r_{x, y}= \frac{\sigma_{x, y}}{\sigma_x \sigma_y}= | |
\frac{E\left( \left(x-\mu_{x})(y-\mu_{y}\right)\right)} | \frac{E\left( \left(x-\mu_{x})(y-\mu_{y}\right)\right)} | ||
{\sqrt{E\left( (x-\mu_{x})^2\right) E\left( (y-\mu_{y})^2\right)}}, | {\sqrt{E\left( (x-\mu_{x})^2\right) E\left( (y-\mu_{y})^2\right)}}, | ||
| Linia 50: | Linia 50: | ||
<math> | <math> | ||
| − | + | r^{2}=\frac{\left( \underset{i=1}{\overset{N}{\sum }}(x_{i}- | |
\overline{x})(y_{i}-\overline{y})\right) ^{2}}{\underset{i=1}{\overset{N}{ | \overline{x})(y_{i}-\overline{y})\right) ^{2}}{\underset{i=1}{\overset{N}{ | ||
\sum }}(x_{i}-\overline{x})^{2}\underset{i=1}{\overset{N}{\sum }}(y_{i}- | \sum }}(x_{i}-\overline{x})^{2}\underset{i=1}{\overset{N}{\sum }}(y_{i}- | ||
| Linia 84: | Linia 84: | ||
)(y_{i}-\overline{y})\right) ^{2}}{\underset{i=1}{\overset{N}{\sum }}(x_{i}- | )(y_{i}-\overline{y})\right) ^{2}}{\underset{i=1}{\overset{N}{\sum }}(x_{i}- | ||
\overline{x})^{2}}\frac{\underset{i=1}{\overset{N}{\sum }}(y_{i}-\overline{y} | \overline{x})^{2}}\frac{\underset{i=1}{\overset{N}{\sum }}(y_{i}-\overline{y} | ||
| − | )^{2}}{\underset{i=1}{\overset{N}{\sum }}(y_{i}-\overline{y})^{2}}= | + | )^{2}}{\underset{i=1}{\overset{N}{\sum }}(y_{i}-\overline{y})^{2}}=r^{2} |
\underset{i=1}{\overset{N}{\sum }}(y_{i}-\overline{y})^{2} | \underset{i=1}{\overset{N}{\sum }}(y_{i}-\overline{y})^{2} | ||
</math> | </math> | ||
| Linia 91: | Linia 91: | ||
<math> | <math> | ||
| − | { | + | {r^{2}=\frac{\underset{i=1}{\overset{N}{\sum }}(y_{i}^{p}- |
\overline{y})^{2}}{\underset{i=1}{\overset{N}{\sum }}(y_{i}-\overline{y})^{2} | \overline{y})^{2}}{\underset{i=1}{\overset{N}{\sum }}(y_{i}-\overline{y})^{2} | ||
}\ } | }\ } | ||
Wersja z 06:41, 20 maj 2022
Wnioskowanie_Statystyczne_-_wykład
Interpretacja współczynnika korelacji liniowej
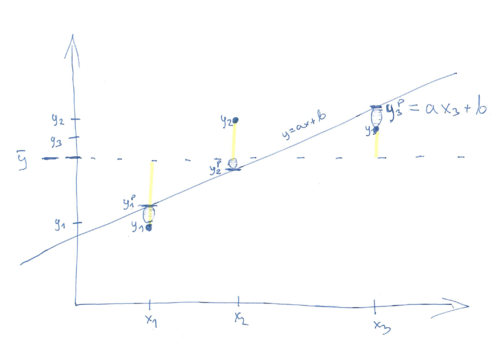
Rozważmy wariancję zmiennej [math]y[/math] z poprzedniego rozdziału. Niech [math]y_{i}^{p}=a+bx_{i}[/math]
[math]
\underset{i=1}{\overset{N}{\sum }}(y_{i}-\overline{y})^{2}=
\underset{i=1}{\overset{N}{\sum }}(y_{i}-y_{i}^{p}+y_{i}^{p}-\overline{y}
)^{2}=
[/math]
[math]
\underset{i=1}{\overset{N}{\sum }}(y_{i}-y_{i}^{p})^{2}+\underset{i=1}{
\overset{N}{\sum }}(y_{i}^{p}-\overline{y})^{2}+2\underset{i=1}{\overset{N}{
\sum }}(y_{i}-y_{i}^{p})(y_{i}^{p}-\overline{y})
[/math]
Całkowitą wariancię zmiennej [math]y[/math] podzieliliśmy na dwa człony: wariancję estymaty [math]y_{i}^{p}[/math] wokół wartości średniej [math]\overline{y}[/math] i wariancję obserwowanych [math]y_{i}[/math] wokół estymaty [math]y_{i}^{p}[/math] (trzeci człon znika).
Współczynnik korelacji liniowej (Pearsona)
przypominamy wyprowadzone w poprzednim rozdziale zależności:
[math]
b=\frac{\underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x})(y_{i}-
\overline{y})}{\underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x})^{2}},
\qquad a=\overline{y}-b\overline{x}
[/math]
oraz estymator współczynnika korelacji liniowej
[math] r_{x, y}= \frac{\sigma_{x, y}}{\sigma_x \sigma_y}= \frac{E\left( \left(x-\mu_{x})(y-\mu_{y}\right)\right)} {\sqrt{E\left( (x-\mu_{x})^2\right) E\left( (y-\mu_{y})^2\right)}}, [/math]
jego kwadrat estymujemy jako
[math] r^{2}=\frac{\left( \underset{i=1}{\overset{N}{\sum }}(x_{i}- \overline{x})(y_{i}-\overline{y})\right) ^{2}}{\underset{i=1}{\overset{N}{ \sum }}(x_{i}-\overline{x})^{2}\underset{i=1}{\overset{N}{\sum }}(y_{i}- \overline{y})^{2}} [/math]
Ponieważ
[math]
\forall_i (y_i - \overline{y}) =
b (x_i - \overline{x} )
[/math],
[math]
\underset{i=1}{\overset{N}{\sum }}(y_{i}^{p}-\overline{y})^{2}=
[/math]
[math]= b^{2} \underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x})^{2}= [/math]
[math] =\frac{\left( \underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x})(y_{i}-\overline{y} )\right) ^{2}}{\left( \underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x} )^{2}\right) ^{2}}\underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x} )^{2}= [/math]
[math] =\frac{\left( \underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x} )(y_{i}-\overline{y})\right) ^{2}}{\underset{i=1}{\overset{N}{\sum }}(x_{i}- \overline{x})^{2}}\frac{\underset{i=1}{\overset{N}{\sum }}(y_{i}-\overline{y} )^{2}}{\underset{i=1}{\overset{N}{\sum }}(y_{i}-\overline{y})^{2}}=r^{2} \underset{i=1}{\overset{N}{\sum }}(y_{i}-\overline{y})^{2} [/math]
czyli
[math] {r^{2}=\frac{\underset{i=1}{\overset{N}{\sum }}(y_{i}^{p}- \overline{y})^{2}}{\underset{i=1}{\overset{N}{\sum }}(y_{i}-\overline{y})^{2} }\ } [/math]
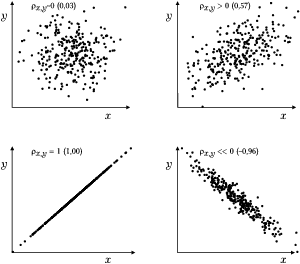
przykłady interpretacji podaje też artykuł z Wikipedii