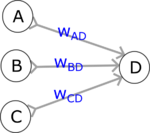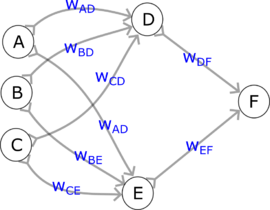TI/Sztuczne sieci neuronowe: Różnice pomiędzy wersjami
| Linia 1: | Linia 1: | ||
| − | ==[["Technologia_informacyjna"|⬆]] | + | ==[["Technologia_informacyjna"|⬆]] Obliczenia w sztucznej sieci neuronowej== |
[[Plik:Neuron.png|bezramki|150px|right|Sztuczny neuron czyli prosty sumator]] | [[Plik:Neuron.png|bezramki|150px|right|Sztuczny neuron czyli prosty sumator]] | ||
| Linia 25: | Linia 25: | ||
| − | [[Plik:MnistExamplesModified.png|ramka| | + | ==Przykład: rozpoznawanie cyfr za pomocą prostej sieci== |
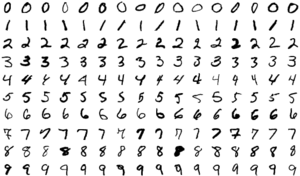
| + | [[Plik:MnistExamplesModified.png|mały|ramka|Przykłady z bazy [https://yann.lecun.com/exdb/mnist/ MNIST], źródło: [https://en.wikipedia.org/wiki/MNIST_database Wikipedia]]] | ||
| + | Strukturę sieci dopasowujemy do wymiarów problemu. | ||
| + | |||
| + | ====Wartwa wejściowa==== | ||
| + | przyjmuje dane; jeśli sieć ma rozpoznawać obrazy w odcieniach szarości, na wejściu podamy liczby odpowiadające zaczernieniu kolejnych pikseli — dla obrazów o wymiarach 28*28 pikseli będzie ich 784. | ||
| + | |||
| + | ====Wartwa wyjściowa==== | ||
| + | — jej rozmiar zależy od formy oczekiwanych "odpowiedzi". Jeśli mają to być odpowiedzi tak/nie (np. na obrazku znajduje się szukany obiekt lub nie), wystarczyć może nawet jeden sztuczny neuron wyjściowy: jeśli zwracana wartość będzie mniejsza od jakiegoś progu, przyjmiemy "tak", w przeciwnym przypadku — "nie". | ||
| + | |||
| + | |||
| + | Jeśli sieć ma rozpoznawać znajdujące się na obrazach liczby, najwygodniej przypisać każdej liczbie jeden neuron wartwy wyjściowej. Wtedy "idealną" odpowiedzią sieci na liczbę 9 będzie wartość "1" w ostatnim neuronie, i zera w pozostałych. Takie "wzorcowe" odpowiedzi pojawiają się tylko w procesie uczenia sieci (jako oznaczenia zbioru uczącego), w praktycznym działaniu takiej sieci jako "odpowiedź" wybieramy najwyższą wartość. | ||
| + | |||
Wersja z 11:58, 24 lip 2024
Spis treści
⬆ Obliczenia w sztucznej sieci neuronowej
Sztuczne sieci neuronowe konstruowane są jednostek zwanych "sztucznymi neuronami". Możemy o nich myśleć jako o komórkach pamięci komputera. Konkretna wartość zapisana w jednej takiej komórce (D) jest w każdym kroku obliczana według stałego schematu:
- liczby z komórek (sztycznych neuronów) poprzedniej warstwy ABC są mnożone przed odpowiednie wagi i dodawane do siebie: A * wAD + B * wBD + C * wCD
- wyliczona powyżej suma ważona jest poddawana działaniu funkcji aktywacji f:
D = f (A * wAD + B * wBD + C * wCD)
Spróbujmy teraz prześledzić obliczenia wykonywane przez przykładową sieć:
- W (sztucznych:) neuronach po lewej (ABC) znajdują się wartości (liczby), które dla uproszczenia oznaczymy tymi samymi literami ABC. Mogą one reprezentować wejście sieci (wtedy będzie to "warstwa wejściowa") lub być wynikiem obliczeń poprzednich warst sieci (wtedy będzie to "warstwa ukryta").
- Wartości w neuronach D i E (wartwa ukryta) wyliczamy według podanego powyżej wzoru:
- D = f (A * wAD + B * wBD + C * wCD)
- E = f (A * wAE + B * wBE + C * wCE)
- W następnym kroku wyliczamy wartość dla neuronu ostatniej warstwy F:
- F = f (D * wDF + E * wEF)
Wyliczoną w ten sposób wartość F możemy uznać za "odpowiedź" tej sieci na podane na wejściu liczby A, B, i C.
Sztuczna sieć neuronowa sieć jest jednoznacznie określona przez strukturę połączeń oraz konkretne wartości wag wXY, zwanych też parametrami sieci lub modelu; w roku 2024 liczby parametrów dużych modeli sięgają setek miliardów.
Przykład: rozpoznawanie cyfr za pomocą prostej sieci
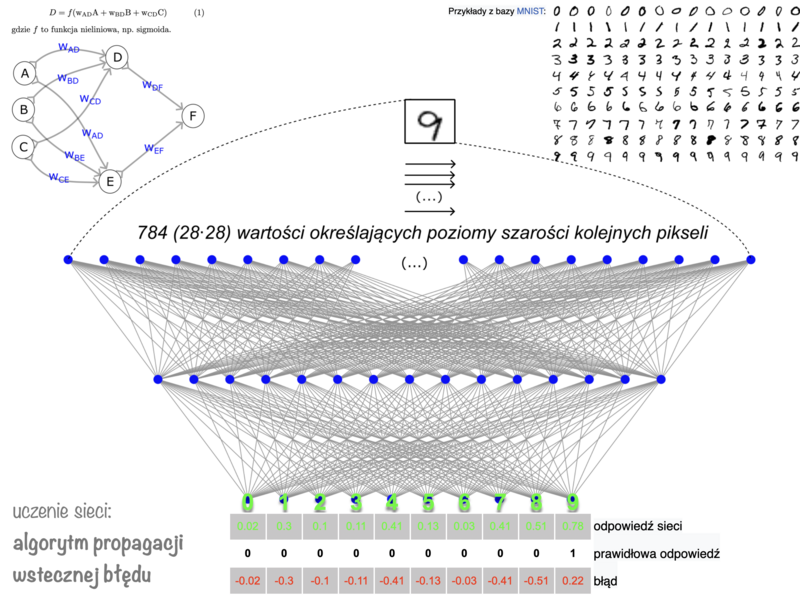
Strukturę sieci dopasowujemy do wymiarów problemu.
Wartwa wejściowa
przyjmuje dane; jeśli sieć ma rozpoznawać obrazy w odcieniach szarości, na wejściu podamy liczby odpowiadające zaczernieniu kolejnych pikseli — dla obrazów o wymiarach 28*28 pikseli będzie ich 784.
Wartwa wyjściowa
— jej rozmiar zależy od formy oczekiwanych "odpowiedzi". Jeśli mają to być odpowiedzi tak/nie (np. na obrazku znajduje się szukany obiekt lub nie), wystarczyć może nawet jeden sztuczny neuron wyjściowy: jeśli zwracana wartość będzie mniejsza od jakiegoś progu, przyjmiemy "tak", w przeciwnym przypadku — "nie".
Jeśli sieć ma rozpoznawać znajdujące się na obrazach liczby, najwygodniej przypisać każdej liczbie jeden neuron wartwy wyjściowej. Wtedy "idealną" odpowiedzią sieci na liczbę 9 będzie wartość "1" w ostatnim neuronie, i zera w pozostałych. Takie "wzorcowe" odpowiedzi pojawiają się tylko w procesie uczenia sieci (jako oznaczenia zbioru uczącego), w praktycznym działaniu takiej sieci jako "odpowiedź" wybieramy najwyższą wartość.