FizykaI FMiN/Wprowadzenie

Wprowadzenie

Czym zajmuje się fizyka ?

Fizyka zajmuje się badaniem najbardziej fundamentalnych i uniwersalnych właściwości materii i zjawisk w otaczającym nas świecie. Dobrze podsumowuje to poniższy cytat:

"Nasza wiedza o świecie fizycznym dzieli się na dwie kategorie: prawa przyrody i warunki początkowe. Fizyka w pewnym sensie nie interesuje się warunkami początkowymi, pozostawiając je badaniom astronomów, geologów, geografów, i tak dalej."
Eugene Wigner

Staramy się znaleźć prawidłowości niezależne od "warunków początkowych". Okazuje się, że te same prawa pozwalają czasami wyjaśnić zupełnie różne zjawiska.

Dlatego staramy się zrozumieć zjawiska zachodzące zarówno na najmniejszych jak i na największych odległościach:

Szukamy praw opisujących zarówno zachowanie najmniejszych cząstek elementarnych oraz ewolucję wszechświata.

Prawa fizyki, które będziemy poznawać w ramach tego wykładu są właśnie takimi uniwersalnymi prawami (choć o ich ograniczeniach też będziemy mówić).

Budowa materii

Materia, którą badamy w doświadczeniach składa się z cząsteczek związków chemicznych bądź pojedyńczych atomów. Wiemy jednak, że atomy sa podzielne. Najmniejsze znane obecnie cząstki, z których złozona jest cała otaczająca nas materia to elektrony i kwarki (tzw. cząstki fundamentalne). Cząstki te są tak małe, że ich rozmiarów dotychczas nie udało nam się zmierzyć.

Rozmiary składników materii

składnik	rozmiar	zbudowany z
kryształ	[math]\unit{{10^{-3}}{m}}[/math]	atomów lub cząsteczek
cząsteczka chemiczna	[math]10^{-9} \text{m}[/math]	atomów
pojedynczy atom	[math]10^{-10} \text{m}[/math]	jądra atmowego i elektronów
jądro atomowe	[math]10^{-14} \text{m}[/math]	protonów i neutronów
protony i neutrony	[math]10^{-15} \text{m}[/math]	kwarków
kwarki i elektrony	[math] \lt 10^{-18} \text{m}[/math]

Rola doświadczenia

Skoro chcemy opisać otaczający nas świat (a nie jakąś rzeczywistość wirtualną) to oznacza, że niezbędnym elementem i punktem wyjścia wszystkich naszych rozważań powinno być doświadczenie.

Doświadczenie dostarcza nam danych, na podstawie których staramy się tworzyć modele opisujące rzeczywistość.

Następnie od opisu zjawiska (model opisowy) staramy się przejść do wyjaśnienia jego mechanizmu - tworzymy model przyczynowy("teorię")

Przykład:

ruch planet ⇒ prawa Keplera ⇒ prawo grawitacji Newtona

Do tworzenia modeli wrócimy w dalszej części tego rozdziału.

Pomiary w fizyce

Wynikiem każdego doświadczenia jest pomiar, który może jednak mieć różny charakter. Dobrze jest się zastanowić z jakimi typami pomiarów możemy mieć do czynienia.

Zliczanie

Przykłady:

• liczba grzybów w barszczu
• liczba kropel deszczu na szybie (w określonym okresie czasu)
• liczba rozpadów w próbce promieniotwórczej
• liczba cząstek wyprodukowanych w zderzeniach wysokiej energii

Liczymy jakieś elementy lub zdarzenia, w określonym przedziale czasu lub przestrzeni.

Szczególny przypadek — niewielka liczba możliwych wyników pomiaru:

• rzut kostką do gry
• pomiar stanu skupienia substancji

(ciało stałe, ciecz lub gaz)

• rozpad pojedyńczego jądra atomowego

(rozpadł się albo nie)

• układy z dyskretnymi stanami dozwolonymi
  

(w szczególności układy kwantowe, np. atomy)

Pomiary ilościowe

Pomiary, których wynik wyrażamy poprzez podanie wartości liczbowej i jednostki.

Przykłady:

• długość stołu

przykładowo: 5,73 m

• masa ciała

np. 88 kg

• czas trwania wykładu

np. 45 min.

• natężenie prądu

np. 150 mA

Wartość liczbowa wielkości fizycznej zależy od jednostki, w której jest wyrażona.

Wynik pomiaru porównujemy z przyjętą dla danej wielkości fizycznej jednostką.

Porównywać możemy jedynie wielkości tego samego rodzaju
[math]\Rightarrow[/math] ważne jest jednoznaczne zdefiniowanie jednostek

Układ jednostek SI

SI - (fr) Systéme Internationale

Międzynarodowy układ jednostek wprowadzony w 1960 roku. Definiuje 7 jednostek podstawowych:

Wielkość fizyczna	Jednostka	symbol
Długość	metr	[m]
Masa	kilogram	[kg]
Czas	sekunda	[s]
Natężenie prądu elektrycznego	amper	[A]
Temperatura termodynamiczna	kelwin	[K]
Ilość substancji	mol	[mol]
Światłość	kandela	[cd]

W mechanice kluczowe będą pierwsze 3 z powyższych jednostek. Dlatego przyjrzyjmy się bliżej ich definicji.

1 sekunda

Sekunda jest to czas równy 9 192 631 770 okresom promieniowania emitowanego przez atom [math]^{133}[/math]Cs przy przejściu między dwoma poziomami nadsubtelnymi

Częstość promieniowania dla tej lini cezu wynosi
z definicji 9 192 631 770 Hz.

Historia:

• [math]\frac{1}{86400}[/math] część średniego dnia słonecznego (do 1960)
• odpowiednia część roku tropikalnego (do 1967)

1 metr

1 metr jest zdefiniowany jako odległość jaką pokonuje świato w próżni w czasie równym [math]\nicefrac{1}{299792458}[/math] sekundy

Tym samym prędkość światła została zdefiniowana jako [math]c=299792458 \text{m/s}[/math] (dokładnie !) wybrana wartość zgodna z wcześniejszymi pomiarami

Historia:

• 0.0000001 ([math]10^{-7}[/math]) południka paryskiego, od bieguna do równika
• wzorzec platynowo-irydowy (do 1960)
• wielokrotność długości fali światła [math]^{86}[/math]Kr (do 1983)

1 kilogram

Kilogram jest to masa wzorca jednego kilograma

Platynowo-irydowy wzorzec jednego kilograma przechowywany jest w Międzynarodowym Biurze Miar i Wag w Severes pod Paryżem

Historia

• masa jednego decymetra sześciennego wody (do końca XVIII wieku)

Notacja naukowa

Ułatwia zapisywanie bardzo dużych i bardzo małych liczb:

• prędkość światła:

[math]c\approx 300000000 \text{m/s} = 3 \cdot 10^{8} \text{m/s}[/math]

• rozmiar protonu:

[math]r\sim 0.000000000000001 \text{m}[/math] = [math]10^{-15}\text{m}[/math]

• masa Ziemi:

[math]m_Z \approx 5972000000000000000000000\text{kg} = 5.972 \cdot 10^{24} \text{kg}[/math]

Wykładnik potęgi 10 określa nam "rząd wielkości"

Różnica o rząd wielkości to dużo, 2-3 rzędy to bardzo dużo, 10 rzędów to "przepaść"

Przykład:

stosunek rozmiaru Ziemi do rozmiaru ziarnka piasku to ok. 10 rzędów wielkości

[math]\Leftarrow \; \times 10^{10} \; \Rightarrow[/math]

Jednostki pochodne

Aby dalej uprościć zapis wyników pomiarów używamy odpowiednich przedrostków do zdefiniowania jednostek pochodnych - jednostek, które są określonymi wielokrotnościami jednostki podstawowej. Zdefiniowano następujące mnożniki:

przedrostek	mnożnik	symbol
zwiększające wartość
yotta	[math]10^{24}[/math]	Y
zetta	[math]10^{21}[/math]	Z
exa	[math]10^{18}[/math]	E
peta	[math]10^{15}[/math]	P
tera	[math]10^{12}[/math]	T
giga	[math]10^{9}[/math]	G
mega	[math]10^{6}[/math]	M
kilo	[math]10^{3}[/math]	k
hekto	[math]10^{2}[/math]	h
deka	10	da
zmniejszające wartość
decy	[math]10^{-1}[/math]	d
centy	[math]10^{-2}[/math]	c
mili	[math]10^{-3}[/math]	m
mikro	[math]10^{-6}[/math]	[math]\mu[/math]
nano	[math]10^{-9}[/math]	n
piko	[math]10^{-12}[/math]	p
femto	[math]10^{-15}[/math]	f
atto	[math]10^{-18}[/math]	a
zepto	[math]10^{-21}[/math]	z
yokto	[math]10^{-24}[/math]	y

np. [math]\unit{ 1 }{nm} = \unit{10^{-9}}{ m} = \unit{0.000 000 001}{ m}[/math]

Zamiana jednostek

Przeliczanie jednostek nie może zmieniać wartości wielkości fizycznej.

Ale każdą wartość możemy pomnożyć przez 1 wyrażone poprzez stosunek jednostek.

Na przykład:

[math]\unit{1}{ NM} = \unit{1852}{ m} [/math]⇒ [math] 1 \equiv \frac{\unit{1852}{m}}{\unit{1}{NM}} [/math]

[math]\unit{1}{ h} = \unit{3600}{ s }[/math] ⇒[math] 1 \equiv \frac{\unit{1}{h}}{\unit{3600}{s}} [/math]

Przeliczanie prędkości statku: węzły (kn)[math]\rightarrow[/math] m/s

[math]\begin{array}{rcl} v = \unit{20}{kn} & = & \unit{ 20}{ \frac{NM}{h}} \cdot 1 \cdot 1 \\ & & \\ & = &\unit{ 20}{ \frac{NM}{h}} \cdot \frac{\unit{1852}{ m}}{\unit{1}{NM}} \cdot \frac{\unit{1}{ h}}{\unit{3600}{s}} \\ & & \\ & = & \unit{\frac{20 \cdot 1852}{3600}}{ \frac{m}{s}} \approx \unit{10.3}{ \frac{m}{s}} \end{array}[/math]

Analiza wymiarowa

Zależności między jednostkami są uniwersalne. Każda zależność między wielkościami fizycznymi (prawo przyrody albo wynik zadania) musi je respektować.

Przeliczenie jednostek jest niezbędnym elementem rozwiązywania problemów fizycznych. Jest to bardzo silny test poprawności odpowiedzi!
Niejednokrotnie pozwala "zgadnąć" postać rozwiązania...

Przykład:
Jak zmieniłby się okres obiegu Ziemi do okoła Słońca, gdyby cały nasz świat (Słońce, Ziemia, rozmiary orbity) został zmniejszony 10 razy (przy zachowaniu gęstości materii)?

Mamy: [math] [r_{SZ}]=[R_{S}]=[R_{Z}]=\unit{}{m}, \;\; [\rho_Z]=[\rho_S]=\unit{}{\frac{kg}{m^3}}, \;\; [G_N]=\unit{}{N\cdot\frac{m^2}{kg^2}} = \unit{}{\frac{m^3}{s^2 kg}} [/math]

Szukamy: [math][T] = \unit{}{s}[/math]

Z analizy wymiarowej: [math]T \sim \sqrt{\frac{1}{\rho\;G_N}} \cdot f(r_{SZ},R_S,R_Z) [/math], gdzie [math]f()[/math] - funkcja bezwymiarowa

⇒ może zależeć wyłącznie od stosunków odległości i promieni!

Błędy pomiarowe

Rozkład Poissona

Z rozkładem Poissona mamy do czynienia wtedy, gdy w określonym przedziale (czasu lub przestrzeni) liczymy zdarzenia od siebie niezależne.

Jest to sytuacja z jaką często mamy do czynienia.

Przykład:

liczba rejestrowanych rozpadów promieniotwórczych

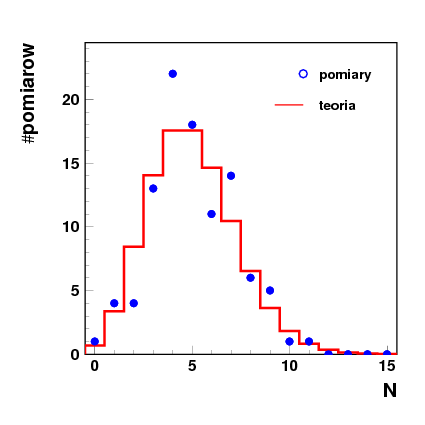
Poniższy rysunek przedstawia zestawienie wyników 100 pomiarów dla źródełka dającego średnio 5 rozpadów na sekundę (każdy pomiar: 1 sekunda; N - liczba zliczeń w jednym pomiarze)

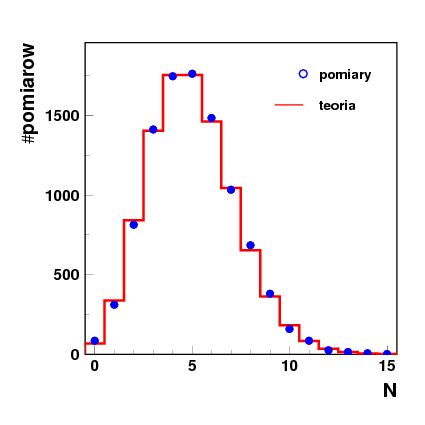
Zestawienie wyników dla 10000 pomiarów:

Prawdopodobieństwo, że w kolejnym pomiarze zarejestrujemy N zliczeń wynosi:

[math] p(N) = \frac{\mu^{N} e^{-\mu}}{N !} [/math]

Jest to właśnie Rozkład Poissona. Ma on tylko jeden parametr: [math]\mu[/math] - wartość oczekiwana rozkładu (średnia liczba obserwowanych rozpadów)

W każdym pomiarze, mimo identycznych warunków początkowych, możemy otrzymać inny wynik. Czasami są to wyniki bardzo rozmieżne od oczekiwanych. Np. dla [math]\mu[/math]=5 możemy zmierzyć

• N=0 rozpadów, z prawdopodobieństwem ok. 0.7 %
• [math]N\ge 10[/math] rozpadów, z prawdopodobieństwem ok. 3.2 %

Pomiar wielkości fizycznej opisanej rozkładem Poissona obarczony jest "naturalnym" błedem statystycznym

błąd [math]\; \sim \; \sqrt{\mu}[/math]

Względna dokładność pomiaru rośnie wraz ze wzrostem [math]\mu[/math]. Dlatego też staramy sie (jeśli to możliwe) wydłużać czas pomiaru...

Rozkład Gaussa

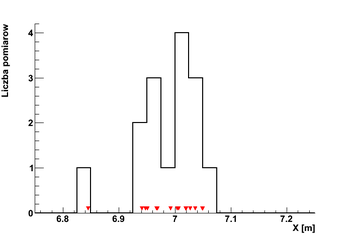
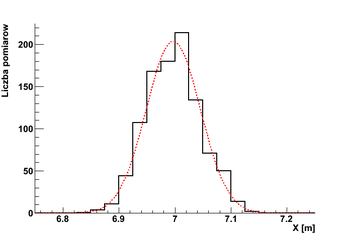
Przykładowe wyniki pomiarów ilościowych: pomiarów długości stołu (15 pomiarów). Czerwone punkty pokazują wyniki poszczególnych pomiarów, tzw. histogram (czarna linia) pokazuje liczbę pomiarów w poszczególnych przedziałach wyniku x.

W przypadku wielkości fizycznych przyjmujących wartości rzeczywiste, wyniki pomiarów mają zazwyczaj rozkład normalny, nazywany też rozkładem Gaussa. Rozkład ten opisuje rozkład wyników pomiarów przy założeniu, że fluktuacje są wynikiem wielu niezależnych zaburzeń.

Przykładowy rozkład dla 1000 pomiarów, porównany z oczekiwanym rozkładem Gaussa:

Prawdopodobieństwo w rozkładzie Gaussa wyraża się wzorem:

[math] p(x) = \frac{1}{\sigma \sqrt{2 \pi}} \;\; e^{-\frac{1}{2}\left( \frac{x-\mu}{\sigma}\right)^2} [/math]

gdzie:
[math]\mu[/math] - wartość oczekiwana rozkładu (wartość prawdziwa, względnie średni wynik bardzo wielu pomiarów)
[math]\sigma[/math] - miara szerokości rozkładu

Dla rozkładu Gaussa wartość [math]\sigma[/math] jest równa tzw. średniemu odchyleniu kwadratowemu. Innymi słowy [math]\sigma^2[/math] jest równe średniej wartości kwadratu odchylenia pomiaru od wartości oczekiwanej:

[math] \sigma^2 = \left\langle (x-\mu)^2 \right\rangle [/math]

W przypadku pomiarów podlegających rozkładowi Gaussa wartość [math]\sigma[/math] uznajemy za błąd pomiaru.

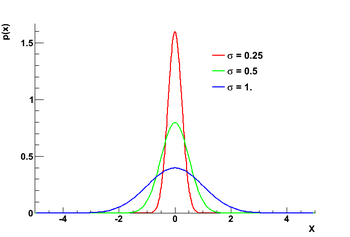
Przykłady rozkładów o [math]\mu = 1 [/math] i różnych wartościach [math]\sigma[/math]:

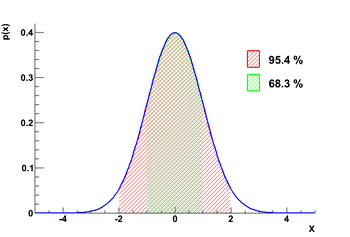
Błąd pomiaru wielkości fizycznej mówi nam o oczekiwanej (średniej kwadratowej) wartości błędu. W ok. 32% przypadków różnica między wartością oczekiwaną i wynikiem pomiaru będzie większa niz [math]1\sigma[/math], w ok. 5% większa niż [math]2\sigma[/math].

Możliwe są jednak wyniki pomiarów, dla których odchylenie od wartości oczekiwanej (wartości prawdziwej) wielkrotnie przekracza wartość błędu! Prawdopodobieńtwa odchylenia większego niż zadana wartość podsumowane są w poniższej tabeli:

odchylenie	prawdopodobieństwo
[math]\pm 1 \sigma[/math]	31.73%
[math]\pm 2 \sigma[/math]	4.55%
[math]\pm 3 \sigma[/math]	0.27%
[math]\pm 4 \sigma[/math]	0.0063%
[math]\pm 5 \sigma[/math]	0.000057%

Błędy przypadkowe (statystyczne)

Omówione powyżej rozkłady Poissona i Gaussa dotyczą błędów przypadkowych. Błędy te wynikają z fluktuacji (losowych zaburzeń) w przebiegu samego zjawiska, lub w procesie mierzenia. Nie wpływają na średni wynik pomiaru (wartość oczekiwaną).

Błędy systematyczne

W ogólnym przypadku musimy się jednak także zastanowić nad tzw. błędami systematycznymi. Są to stałe przesunięcia wyników pomiarów (wartości oczekiwanej rozkładów mierzonych wartości) w stosunku do wartości prawdziwej.

Błąd systematyczny może się pojawić w wyniku:

• złej kalibracji (wyskalowania) urządzenia
• przyjęcia złej metody pomiaru
• zaniedbania istotnych poprawek

Właściwa ocena błędów systematycznych jest jednym z najtrudniejszych aspektów fizyki doświadczalnej...

Modele w fizyce

Punktem wyjścia wszystkich rozważań w fizyce jest doświadczenie. Przeprowadzając pomiary i obserwacje otrzymujemy wyniki liczbowe. Następnie, aby opisać wyniki pomiarów tworzymy modele.

Model opisowy

Procedura tworzenia modelu może wyglądać następująco:

1. przeprowadzamy pomiary
2. analizując ich wyniki poszukujemy parametrów istotnych dla rozważanego zagadnienia, sprawdzamy które warunki początkowe można pominąć, a które nie
3. szukamy zależności funkcyjnej, często poprostu ją zgadujemy (intuicja)
4. dopasowujemy parametry funkcji
5. porównujemy z wynikami pomiarów

jeśli zgodność jest niezadawalająca, cofamy się o jeden lub kilka kroków (możemy także przeprowadzić dodatkowe pomiary).

Przykład: okres drgań wahadła matematycznego

• zależy tylko od długości wahadła [math]l[/math]
  

nie zależy od masy kulki, koloru nici itp...

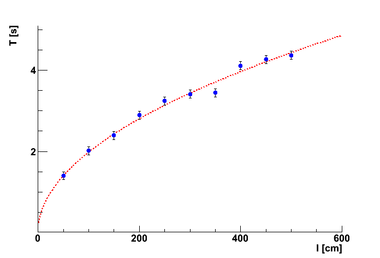
Wyniki pomiarów:

• wyniki dobrze opisuje zależność

  [math] T [s] = A \cdot \sqrt{l\; [\unit{}{m}]} [/math]

  
  

• dopasowanie (zaznaczone na powyższym rysunku) [math] A \; = \; 1.99 \pm 0.07 [/math]

  gdyby nie różnica jednostek sugerowałoby to zależność postaci

  [math] T [s] \; = \; 2 \cdot \sqrt{ \unit{l}{ [m]}} \;\;\; (???) [/math]

  
  

• analiza wymiarowa: jednostki czasu możemy tylko uzyskać wstawiając przyspieszenie ziemskie g. W granicach błędu dopasowana zależność może więc odpowiadać (szukamy najbardziej "naturalnych" współczynników)

  [math] T = \frac{25}{4} \cdot \sqrt{\frac{l}{g}} \;\;\; (???) [/math]

Bez zrozumienia mechanizmu drgań wahadła możemy tylko zwiększać dokładność pomiaru parametru A...

Teoria i doświadczenie

Tworząc modele i teorie staramy się ująć istotę zjawiska. Dlatego często posługujemy się idealizacją (np. punkt materialny, układ izolowany) i/lub uogólniamy wnioski wynikające z doświadczenia. Staramy się też dostrzec uniwersalne zależności, symetrie lub prawa zachowania.

Podstawowe założenia

niezbędne, żeby móc zajmować się fizyką:

• Prawa fizyki są wszędzie takie same.

Nawet w najdalszych zakątkach wszechświata...

• Prawa fizyki nie zmieniają się w czasie.

Są niezmienne od chwili narodzin wszechświata...

Założenia te też wynikają z doświadczenia. Dla przykładu: linie węgla w widmie kwazara PKS 1232+0815 dochodzące do nas z odległegości ok. 12 mld lat świetlnych (wyemitowane 12 mld lat temu!) mają taką samą strukturę jak mierzone w laboratorium.

Model przyczynowy

Staramy się wniknąć w przyczyny obserwowanego zjawiska, mechanizm fizyczny danego procesu.

W przypadku omawianego wahadła matematyczngo przyjmujemy, że:

• ruch odbywa się pod wpływem siły grawitacyjnej [math]\vec{F} = m \vec{g}[/math]
• stosujemy przybliżenie małych wychyleń

Otrzymujemy proste równanie różniczkowe:

[math] l \frac{d^2 \theta}{dt^2} \; = \; -g \; \theta [/math]

Rozwiązanie tego równania prowadzi do wzoru:

[math]\begin{array}{rcl} T & = & 2 \pi \sqrt{\frac{l}{g}} \\[3mm] \frac{2\pi}{\sqrt{g}} & \approx & \unit{ 2,03}{ s\cdot m^{-\frac{1}{2}}} \end{array} [/math]

Tworząc teorię często formułujemy pewne założenia nie wynikające wprost
z doświadczenia, albo sprawdzone tylko w ograniczonym obszarze parametrów (!)

Kierujemy się kryteriami prostoty i elegancji modelu, staramy się dostrzec dodatkowe, głębsze symetrie rozważanego zagadnienia, czasami odwołujemy się także do "naturalności" modelu.

Jednak rozstrzygającym kryterium poprawności modelu jest doświadczenie!

Niestety, doświadczenie nigdy nie udowodni 100% poprawności teorii, gdyż nigdy nie jesteśmy w stanie wykonać wszystkich możliwych pomiarów. Może co najwyżej wskazać zakres jej stosowalności.

Natomiast pojedynczy pomiar może "obalić" teorię (ew. ograniczyć zakres jej stosowalności). Musimy zawsze być przygotowani do rewizji poczynionych założeń!

Przykład:

symetria względem odbicia przestrzennego łamana w oddziaływaniach cząstek elementarnych

Analizując wyniki pomiarów, poszukując opisującego je modelu, trzeba dobrze zastanowić się nad wszystkimi założeniami. Wielokrotnie już obalano najbardziej nawet utrwalone założenia. Szczególna teoria względności jest jednym z przykładów.

Ciekawostka

Nawet najbardziej "oczywiste" założenia: (które przyjmuje w dalszej części wykładu)

• przestrzeń jest trójwymiarowa
• przestrzeń jest płaska

wcale nie muszą być spełnione!

Od kilku lat "modne" w fizyce cząstek stało się poszukiwanie "dodatkowych wymiarów"

Jak dobrze znamy "wymiar" świata w którym żyjemy ?
Czy mogą być więcej niż 3 wymiary przestrzenne ?!

• NIE - jeśli pytamy o nieskończone wymiary
• TAK - jeśli dopuścimy wymiary skończone

Dodatkowe wymiary

Przykład:

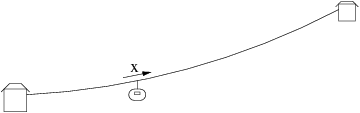
Gdy rozpatrujemy ruch wagonika kolejki linowej przyjmujemy, że lina ma tylko jeden wymiar [math]x[/math]:

Ale dla mrówki, która idzie po tej linie jest to świat dwuwymiarowy:

Jednak w kierunku [math]y[/math] mrówka nie może się oddalić od punktu wyjścia o więcej niż wynosi średnica liny. Idąc dalej wróci do punktu wyjścia. Mówimy, że [math]y[/math] jest współrzędną cykliczna. Dodatkowy wymiar zauważamy dopiero gdy przyglądamy się z rozdzielczością [math]\Delta \lt R[/math]. Z pomiarów grawitacyjnych wykluczono dodatkowe wymiary z [math]R\ge \unit{100}{\mu m}[/math]. Ale w fizyce cząstek wciąż moglibyśmy obserwować efekty dodatkowych wymiarów...

Ogólna klasyfikacja zjawisk

Fizyka nierelatywistyczna ("klasyczna")

Opisuje zachowanie obiektów makroskopowych poruszających się z "umiarkowanymi" prędkościami. Fizyka "dnia codziennego"

Fizyka relatywistyczna

Wkracza wtedy, gdy prędkości względne stają się porównywalne z prędkością światła [math]c\equiv \unit{299\;792\;458}{m/s} \; \; \approx \; \unit{300 \; 000 }{km/s}[/math]

Fizyka współczesna bardzo często wymaga stosowania podejścia relatywistycznego. Bez uwzględnienia efektów relatywistycznych nie jest także możliwe pełne zrozumienie wielu "codziennych" zjawisk, np. oddziaływań magnetycznych!

Fizyka kwantowa

Odejście od zasad fizyki klasycznej następuje też w przypadku obiektów mikroskopowych. Wkracza gdy

[math] \left. \begin{array}{r} \text{energia} \times \text{czas} \\ \text{ped} \times \text{dlugosc} \\ \text{moment pedu} \end{array} \right\} \sim h=\unit{6.626\cdot 10^{-34}}{J \cdot s} [/math]

Przy czym stała Plancka h jest niesłychanie mała. Dla wszelkich obiektów makroskopowych stosujemy fizykę klasyczną. Fizyka kwantowa potrzebna dopiero do opisu zachowania atomów, cząstek itp.

W ramach niniejszego wykładu będziemy się zajmować zjawiskami mechaniki nierelatywistycznej i relatywistycznej.

Nie będziemy analizować zagadnień, do opisu których potrzebna jest mechanika kwantowa.