Wielomiany

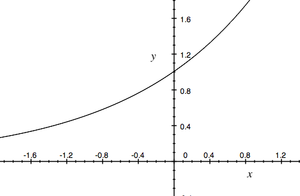
Funkcja wykładnicza

Funkcję wykładniczą definiuje się najsampierw dla wykładników naturalnych. Dla dowolnego [math]a\in \mathbb R \;[/math] oraz [math]n\in \mathbb N \;[/math] można zapisać:

[math]a^n= a\cdot a \dots a \;\;[/math] (n-razy)

Stąd od razu wynika, że:

[math]a^n \cdot a^m = a^{n+m}\;\; [/math]

oraz

[math] \left(a^n\right)^m=a^{n m}\;\; [/math]

Przyjmujemy, że [math]a^0=1\;[/math]. Ujemną potęgę definiujemy rozszerzając zasadę (2) przez dopuszczenie, aby [math]n,m\;[/math] były dowolnymi liczbami całkowitymi. Weźmy: [math] a^{-n} a^n = a^{-n+n}=a^0=1 \;[/math] skąd

[math] a^{-n}=\frac{1}{a^n}\;\; [/math]

(zakładamy tu, że [math]a\ne 0\;[/math]).

Stąd od razu mamy

[math] \left( \frac{a}{b} \right)^n = \frac{a^n}{b^n}\; [/math]

Definiujemy następnie potęgi ułamkowe. Tu zakładamy, że [math]a\gt 0\;[/math] (zaraz się okaże dlaczego).

Oznaczmy: [math]b=a^\frac{1}{n}\;[/math]. Mamy:

[math] b^n = \left( a^\frac{1}{n}\right)^n = a^{\frac{1}{n}\cdot n} = a^1=a \;[/math]

co znaczy, że [math]b=\sqrt[n]{a}\;[/math], czyli

[math] a^\frac{1}{n} = \sqrt[n]{a}.\; [/math]

Dowolną potęgę wymierną liczby [math]a\;[/math] definiujemy teraz jako

[math]a^\frac{p}{n} = (\sqrt[n]{a})^p\; , [/math]

gdzie [math]n\in \mathbb N, p\in \mathbb N\;[/math]

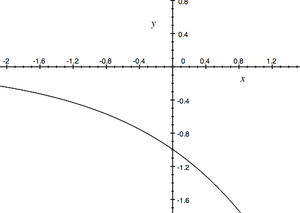
Mamy też: Jeśli [math]a\gt 1\;[/math] i [math]b\gt 0\;[/math], to [math]a^b\gt 1 \;[/math] i, w konsekwencji, jeśli [math]c_1\gt c_2\;[/math], to [math]a^{c_1}\gt a^{c_2}\;[/math]. (Dla [math]a\lt 1\;[/math] znaki trzeba odwrócić). To pozwala przez ciągłość zdefiniować [math]a^b\;[/math] dla dowolnych [math]a\gt 0\;[/math] i [math]b\in \mathbb R\;[/math]. Widać też, że funkcja wykładnicza jest monotoniczna (rosnąca dla [math]a\gt 1\;[/math] i malejąca dla [math]a\lt 1\;[/math]).

Wykres funkcji wykładniczej typu [math]a^x[/math], gdzie a>1

Wykres funkcji wykładniczej typu [math]a^x[/math], gdzie a<1

Funkcja logarytmiczna

Jako że funkcja wykładnicza [math]f(x)=a^x\;[/math] jest rosnąca (weźmy, dla ustalenia uwagi, [math]a\gt 1\;[/math]) w całej swojej dziedzinie, (dziedziną jest [math]\mathbb R\;[/math] a zbiorem wartości [math]\mathbb R_+\;[/math]) to istnieje funkcja do niej odwrotna. Zwiemy ją logarytmem.

Zakładamy, że [math]a\gt 0\;[/math], [math]a\ne 1\;[/math].

Def. Dla danych [math]a\;[/math] oraz [math]y\;[/math], jeśli [math]x\;[/math] jest takie, że [math]a^x=y\;[/math], to [math]x\;[/math] nazywamy logarytmem o podstawie [math]a\;[/math] z [math]y\;[/math] i oznaczamy: [math]x=\log_a y\;[/math]. Dziedziną logarytmu jest [math]\mathbb R_+\;[/math], a zbiorem wartości [math]\mathbb R\;[/math].

Własności

Mamy więc dla dowolnego [math]a\;[/math]: [math]\log_a a = 1\;[/math] (ponieważ [math]a^1 = a\;[/math]) oraz [math]\log_a 1 = 0\;[/math]

(ponieważ [math]a^0=1\;[/math]).

Własności (2) odpowiada:

[math] \log_a(b \cdot c) = \log_a b + \log_a c\;\;[/math] oraz [math]\log_a \tfrac{b}{c} = \log_a b - \log_a c\;\; [/math]

a własności (3):

[math]\log_a b^c = c\cdot \log_a b\;\; [/math]

W szczególności:

[math] \log_a( \sqrt[n]{b}) =\frac{1}{n} \log_a b \; [/math]

Przeliczanie logarytmów o różnych podstawach

Często się zdarza, że trzeba przeliczać logarytmy o różnych podstawach. Najbardziej chyba rozpowszechnione są logarytmy dziesiętne (tzn. o podstawie 10) i naturalne o podstawie [math]e\approx 2,718...\;[/math] (o liczbie [math]e\;[/math] powiemy więcej za kilka wykładów).

Jak przeliczać jedne na drugie?

Rozważmy ogólniejszą sytuację — logarytmów o dwóch podstawach [math]a\;[/math] oraz [math]b\;[/math].

Wyraźmy teraz [math]\log_ax \;[/math] przez [math]\log_b x\;[/math].

Wyraźmy najsampierw [math]a\;\;[/math] jako pewną potęgę [math]b\;\;[/math]. Napiszmy: [math]a = b^A\;\;[/math] i obustronnie zlogarytmujmy. Mamy: [math]\log_a a = 1 = \log_a (b^A) = A\log_a b\;\;[/math], skąd [math] A=\frac{1}{\log_a b}\;[/math]

Weźmy teraz: [math]y=a^x\;[/math]; mamy więc: [math]x=\log_a y\;[/math]. Z drugiej strony, [math]\log_b y = \log_b(b^{Ax}) = Ax = \frac{1}{\log_a b} x\;[/math] czyli

[math]\log_a b \log_b y = \log_a y\;\;[/math]

Przykład

Biorąc [math]a=e\;[/math], [math]b=10\;[/math], mamy: [math]\ln y = \ln 10 \log_{10} y \approx 2,303 \log_{10} y\;[/math].