Reprezentacje przybliżone

Przybliżenia adaptacyjne (adaptive approximations)

Zrozumieć w kulturze europejskiej znaczy często powiedzieć własnymi słowami. Podobnie analiza funkcji polegać może na jej przedstawieniu—lub przybliżeniu—za pomocą funkcji o znanych właściwościach. Kontynuując tę analogię, zbiór znanych funkcji, z pomocą których będziemy chcieli wytłumaczyć funkcję nieznaną, nazwiemy słownikiem. Szczególnym przypadkiem słownika jest baza ortogonalna—najmniejszy kompletny słownik.

Z pomocą niewielu prostych i podstawowych słów można wytłumaczyć niemal dowolnie skomplikowane idee. Jednak opis z użyciem ubogiego słownika nie będzie zwięzły ani elegancki. Dla trafnego wyrażenia subtelnych i nieuchwytnych idei—bądź słabych i przejściowych składowych sygnału—potrzebujemy obszerniejszego słownika, wzbogaconego o wyrażenia fachowe lub licencję poetycką. W analizie sygnałów słownik możemy rozszerzać niemal dowolnie—wystarczy sparametryzować ogólną postać funkcji składowych.

Dokładny opis sygnału (tj. badanej funkcji) w słowniku większym niż baza wprowadza redundancję. Zwięzłość osiągnąć możemy godząc się na przybliżenie sygnału, ale za to z pomocą możliwie niewielkiej ilości funkcji. Jeśli ilość wybranych do reprezentacji sygnału funkcji słownika nazwiemy rozmiarem reprezentacji, to dążyć będziemy zwykle do sytuacji, w której:

rozmiar~reprezentacji wymiar~bazy [math]\ll[/math] rozmiar~słownika

Reprezentację optymalną możemy określić jako taki podzbiór elementów słownika, którego liniowa kombinacja tłumaczy największy procent energii sygnału wśród wszystkich podzbiorów o tej samej liczebności. Wybór takiej reprezentacji jest obliczeniowo NP-trudny, toteż w praktyce zadowalamy się iteracyjnym rozwiązaniem sub-optymalnym—zaproponowanym w 1993 przez S. Mallata i Z. Zhanga algorytmem Matching Pursuit (MP).

W analizie sygnałów używamy zwykle słowników złożonych z funkcji Gabora (Gauss modulowany sinusem) ze względu na ich optymalną lokalizację w przestrzeni czas-częstość. Reprezentacja złożona z funkcji Gabora pozwala również na konstrukcję eleganckiej estymaty gęstości energii sygnału w przestrzeni czas-częstość, usuwającej a priori problem wyrazów mieszanych obecny w tego typu dystrybucjach.

Algorytm matching pursuit i słowniki czas-częstość

Niech dany będzie (słownik) zbiór funkcji (słownik) [math]D = \{g_1, g_2, \ldots, g_n\}[/math] takich, że [math]||g_i||=1[/math]. Algorytm Matching Pursuit (MP) jest procedurą iteracyjną. W pierwszym kroku wybierana jest funkcja [math]g_{\gamma_0}[/math] dająca największy iloczyn skalarny z sygnałem [math]s[/math], po czym w każdym następnym kroku funkcja [math]g_{\gamma_n}[/math] jest analogicznie dopasowywana do residuum sygnału [math]R^n s[/math], pozostałego po odjęciu wyniku poprzedniej iteracji:

[math] \left \{ \begin{array}{l} R^0s=s; \\ R^ns=\langle R^ns,g_{\gamma_n} \rangle g_{\gamma_n}+R^{n+1}s\\ g_{\gamma_n}=\arg \max_{g_{\gamma_i} \in D } |\langle R^ns, g_{\gamma_i}\rangle | \end{array} \right . [/math]

Ortogonalność [math]R^{n+1} s[/math] i [math]g_{\gamma_n}[/math] w każdym kroku procedury implikuje zachowanie energii:

[math] ||s||^2 =\sum_{n=0}^{m-1} {|\langle R^n s, \;g_{\gamma_n}\rangle |^2} + ||R^m s||^2 [/math]

Jeśli słownik [math]D[/math] jest kompletny, procedura zbiega do~[math]f[/math]:

[math] s=\sum_{n=0}^\infty {\langle R^n s,\; g_{\gamma_n}\rangle g_{\gamma_n} } [/math]

Dyskretny słownik funkcji Gabora

Funkcję (atom) słownika czasowo-częstościowego można wyrazić jako translację ([math]u[/math]), rozciągnięcie ([math]s[/math]) i modulację ([math]\omega[/math]) funkcji okna [math]g(t) \in L^2(R)[/math] [math] g_\gamma (t) = \frac {1} {\sqrt{s}} g \left ( \frac {t - u} {s} \right ) e^{i \omega t} [/math]. Optymalną lokalizację w przestrzeni czas-częstość otrzymujemy dla Gaussowskiej obwiedni [math]g(t)[/math], co w przypadku analizy sygnałów o wartościach rzeczywistych daje słownik rzeczywistych atomów Gabora:

[math] g_{\gamma(t)}=K(\gamma,\phi ) e^{-\pi\left( \frac{t-u}{s}\right)^2} \sin(\omega (t-u)+\phi )) [/math]

[math] K(\gamma, \phi)[/math] zapewnia normalizację [math]||g_{\gamma,\phi}||=1[/math]. Pomimo, że analizujemy sygnały dyskretne, parametry dopasowywanych funkcji mogą przyjmować wartości z przedziałów ciągłych. W praktyce korzystamy z relatywnie małych podzbiorów przestrzeni parametrów [math]\gamma~=~\{u,~s,~\omega\}[/math].

Gęstość energii w przestrzeni czas-częstość

Z definicji transformaty Wignera i reprezentacji sygnału w postaci sumy dopasowanych przez algorytm funkcji Gabora (równanie %i 1) możemy skonstruować estymatę gęstości energii sygnału w przestrzeni czas-częstość. Transformata Wignera równania (%i 1) daje

[math] \mathcal{W}_s = \sum_{n=0}^\infty |\langle R^n s, \;g_{\gamma_n}\rangle |^2 \mathcal{W}_{g_{\gamma_n}} + \sum_{n=0}^\infty \; \sum_{m\not=n} \langle R^n s,\; g_{\gamma_n} \rangle \overline{\langle R^m s, \; g_{\gamma_m}\rangle} \mathcal{W}_{g_{\gamma_n}, g_{\gamma_m}} [/math]

Podwójna suma zawiera wyrazy mieszane, znacząco fałszujące obraz rozkładu energii sygnału w klasycznej transformacie Wignera i pochodnych; minimalizacja ich wkładu w tych rozkładach jest przedmiotem zastosowań zaawansowanych technik matematycznych. Dzięki rozkładowi sygnału postaci równania (%i 1), możliwe jest ich usunięcie explicite — po prostu pomijamy podwójną sumę, definiując wielkość [math]E s (t,\omega)[/math]:

[math] E s (t, \omega) = \sum_{n=0}^\infty |\langle R^n s, \;g_{\gamma_n}\rangle |^2 \; \mathcal{W}_{g_{\gamma_n} (t, \omega)} [/math]

Dystrybucja Wignera pojedynczego atomu [math]g_\gamma[/math] spełnia [math] \int _{-\infty}^{+\infty} \int _{-\infty}^{+\infty} \mathcal{W}_{g_{\gamma} (t, \omega)} d t d \omega = ||g_{\gamma}||^2 = 1 [/math] co w połączeniu z zachowaniem energii rozwinięcia MP (1) daje

[math] \int _{-\infty}^{+\infty} \int _{-\infty}^{+\infty} E s (t, \omega) d t d \omega = ||s||^2 [/math]

Uzasadnia to interpretację wielkości [math]E s(t,\omega)[/math] jako gęstości energii sygnału [math]s(t)[/math] w przestrzeni czas-częstość.

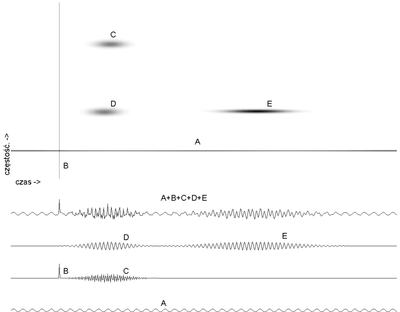
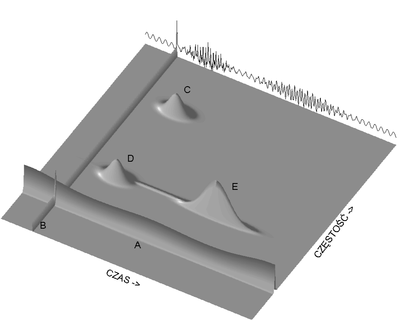
Wynik działania algorytmu ze słownikiem funkcji Gabora ilustrują rysunki %i 1 i %i 3; sygnał zasymulowano jako sumę sinusa, delty Diraca (jednopunktowej nieciągłości) i trzech funkcji Gabora o parami jednakowych położeniach w czasie i częstościach.

Rysunki %i 2 i %i 4 przedstawiają dekompozycję sygnału symulowanego na rysunku %i 1, ale z dodanym liniowo szumem o energii dwukrotnie większej niż sam sygnał.

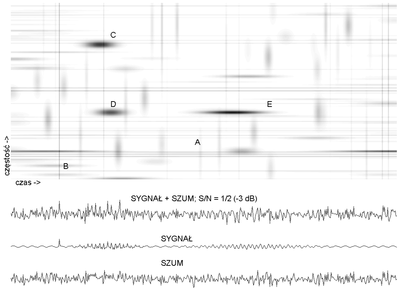Uzyskana z rozkładu MP gęstość energii sygnału w przestrzeni czas-częstość, proporcjonalna do stopnia szarości.	Dekompozycja sygnału z rys. %i 1 z liniowym dodatkiem szumu o dwukrotnie większej energii [math](S/N = -3 dB)[/math].
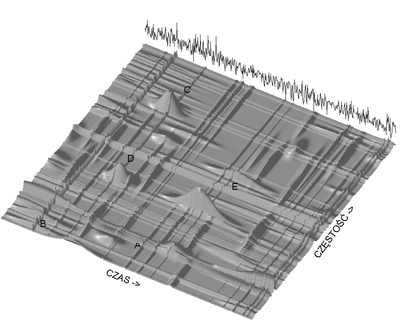Uzyskana z rozkładu MP gęstość energii sygnału w przestrzeni czas-częstość, proporcjonalna do wysokości powierzchni.	Dekompozycja sygnału z rys. %i 1 z liniowym dodatkiem szumu o dwukrotnie większej energii — widok 3D gęstości energii[math](S/N = -3 dB)[/math].

Zastosowanie MP do analizy EEG: czasowo-częstościowa gęstość energii sygnału obliczona z rozkładu MP dwudziestu sekund zapisu EEG w czasie snu. Oznaczone plamy odpowiadają wrzecionom snu. Struktury C-D i E-F zostały oznaczone w sygnale przez eksperta oglądającego sygnał jako pojedyncze wrzeciona.

Wielozmienny algorytm MP (Multivariate matching pursuit, MMP)

W sygnale wielozmiennym (ang. multivariate) pojedynczą próbkę zastępuje wektor wartości opisujących stan układu w danej chwili czasu, jak jak na przykład szereg parametrów opisujących stan gospodarki w danych momentach, czy też potencjał EEG mierzony z wielu elektrod jednocześnie. Jeśli chcemy w takich sygnałach szukać cech wspólnych, na przykład tych samych struktur czas-częstość występujących w sąsiednich kanałach zapisu EEG, musimy ustalić więzy określające które z parametrów funkcji dopasowywanych w każdej iteracji muszą być jednakowe (np. położenie w czasie i szerokość), a które mogą się się różnić w sąsiednich kanałąch (w sposób oczywisty różne będą amplitudy, ale może się teżzmieniać np. faza). Więcej o algorytmach klasy MMP znaleźć można w ksiące (Durka 2007)

Literatura

• S. Mallat and Z. Zhang (1993) Matching pursuit with time-frequency dictionaries. IEEE Transactions on Signal Processing, 41:3397-3415.
• Piotr J. Durka (2007) Matching pursuit. Scholarpedia, 2(11):2288
• P.J. Durka, D. Ircha, and K.J. Blinowska (2001) Stochastic Time-Frequency Dictionaries for Matching Pursuit, IEEE Transactions on Signal Processing, vol. 49, no. 3, pp. 507–510.
• R. Gribonval (2003) Piecewise Linear Source Separation, Proc. SPIE 03, San Diego, CA.
• P.J. Durka (2007) Matching Pursuit and Unification in EEG Analysis, Artech House, ISBN 978-1-58053-304-1.
• P.J. Durka, A. Matysiak, E. Martinez Montes, P. Valdes Sosa, K.J. Blinowska (2005) Multichannel matching pursuit and EEG inverse solutions. Journal of Neuroscience Methods, vol. 148/1, pp. 49-59.

---