Transformata Wignera

AS/ Transformata Wignera

Dla sygnałów niestacjonarnych moc widmowa nie musi być stała w czasie, gdyż zawartość częstości może się zmieniać. Analiza tego typu sytuacji wymaga śledzenia zmian gęstości energii sygnału jednocześnie w czasie i częstości. Pierwszym pomysłem będzie usunięcie ze (wzoru na moc widmową w twierdzeniu Wienera-Chinczyna):

[math] \int e^{-i\omega \tau} \left( \int f(t) f(t+\tau) dt \right) d\tau [/math]

całki po czasie. Dostaniemy w ten sposób funkcję zależną explicite od czasu i częstości — transformatę Wignera-de Ville'a:

[math] \mathcal{W}_s(t, \omega)=\int s \bigl (t + \frac{\tau}{2} \bigr)\; \overline{ s\bigl(t- \frac{\tau}{2} \bigr )\; } e^{- i \omega \tau } d \tau [/math]

Reprezentacja tej postaci ma podstawowe zalety:

• zachowuje energię sygnału,
• wartości brzegowe: wycałkowana po czasie [math]\mathcal{W}_s[/math] daje kwadrat modułu transformaty Fouriera [math]|s(\omega)|^2[/math], a wycałkowana po częsctości — [math]|s(t)|^2[/math],

oraz wady:

• może być ujemna,
• zawiera wyrazy mieszane .

Wyrazy mieszane (cross-terms )

Problem ten występuje (z różnym natężeniem) we wszystkich kwadratowych reprezentacjach energii sygnału w przestrzeni czas-częstość; w transformacie Wignera efekt ten jest najbardziej bezpośredni.

Przypomnijmy wzór na kwadrat sumy: [math](a+b)^2=a^2+b^2+2ab[/math]. Obliczając kwadratową transformatę sygnału złożonego z sumy elementów [math]a[/math] i [math]b[/math], dostaniemy reprezentację występujących w sygnale składników [math]a[/math] i [math]b[/math] oraz wyraz mieszany [math]2ab[/math], który może pojawić się w takim rejonie przestrzeni czas-częstość, że w odpowiadającym mu przedziale czasu w sygnale brak jakiejkolwiek aktywności.

Sygnał złożony z dwóch sinusów o różnych częstościach (dolny wykres) i moduł jego transformaty Wignera przedstawiony w przestrzeni czas-częstość w odcieniach szarości (powyżej, oś częstości skierowana ku górze). Obserwujemy prawidłowe odtworzenie częstości w okolicy występowania sinusów oraz wyraz mieszany (w środku), występujący w odcinku czasu w którym sygnał jest płaski. Wartości transformaty Wignera w rejonie tej struktury oscylują, co umożliwia zachowanie wartości brzegowych całek po czasie i częstości.

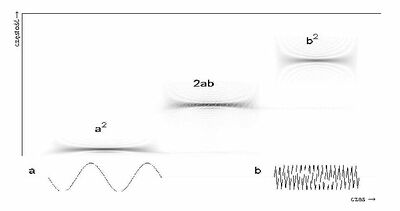
Jednym z głównych zastosowań rozkładów gęstości energii sygnału w przestrzeni czas-częstość (jak ten na rys. %i 1) jest próba odgadnięcia struktury lub własności nieznanego sygnału. W takim przypadku wyrazy mieszane są wysoce mylące — na podstawie samego rozkładu energii z rys. %i 1 moglibyśmy podejrzewać, że w analizowanym sygnale, pomiędzy [math]a[/math] i [math]b[/math], znajduje się jeszcze jedna struktura o pośredniej częstości!

Dla zminimalizowania tego efektu możemy wykorzystać spostrzeżenie, że wyrazy mieszane zwykle silnie oscylują, więc lokalne uśrednienie rozkładu (po czasie i częstości) powinno zmniejszyć ich wkład. Różne realizacje tego uśredniania tworzą bogatą klasę rozkładów o zredukowanych interferencjach (ang. reduced interference distributions, RID ), z których każdy może dawać lepsze od innych rezultaty dla pewnej klasy sygnałów. Jednak w każdym przypadku mamy do czynienia z ogólną prawidłowością: im mniejszy wpływ interferencji

(silniejsze uśrednianie) tym gorsza rozdzielczość.