Pracownia EEG/SSVEP 1: Różnice pomiędzy wersjami
(→Wstęp) |
|||
| (Nie pokazano 8 wersji utworzonych przez 2 użytkowników) | |||
| Linia 82: | Linia 82: | ||
=Ćwiczenia eksperymentalne= | =Ćwiczenia eksperymentalne= | ||
| + | |||
| + | |||
Do rejestracji zjawiska SSVEP wykorzystamy ten sam zestaw eksperymentalny co w przypadku badania Potencjałów Wywołanych. Poniżej przypominamy schemat komunikacji w języku Python pomiędzy komputerem a mikrokontrolerem sterującym wyświetlaniem bodźców. Czcionką pogrubioną wyszczególniono fragment kodu, który jest niezbędny do wytworzenia szybko powtarzających się bodźców świetlnych. | Do rejestracji zjawiska SSVEP wykorzystamy ten sam zestaw eksperymentalny co w przypadku badania Potencjałów Wywołanych. Poniżej przypominamy schemat komunikacji w języku Python pomiędzy komputerem a mikrokontrolerem sterującym wyświetlaniem bodźców. Czcionką pogrubioną wyszczególniono fragment kodu, który jest niezbędny do wytworzenia szybko powtarzających się bodźców świetlnych. | ||
* Po podłączeniu przejściówki USB/RS232 do komputera mikrokontrolera sprawdź jaki plik w katalogu <tt>/dev</tt> został utworzony i przydzielony do urządzenia. | * Po podłączeniu przejściówki USB/RS232 do komputera mikrokontrolera sprawdź jaki plik w katalogu <tt>/dev</tt> został utworzony i przydzielony do urządzenia. | ||
| + | * poproś osobę prowadzącą aby dodała cię do grupy plugdev | ||
| + | sudo usermod -a -G plugdev userName | ||
* Zaimportuj bibliotekę do komunikacji z mikrokontrolerem: | * Zaimportuj bibliotekę do komunikacji z mikrokontrolerem: | ||
: <tt>import SerialPort as SP</tt> | : <tt>import SerialPort as SP</tt> | ||
| Linia 103: | Linia 107: | ||
Kod biblioteki do komunikacji z mikrokontrolerem:<br> | Kod biblioteki do komunikacji z mikrokontrolerem:<br> | ||
| + | |||
<source lang="python"> | <source lang="python"> | ||
| + | # -*- coding: cp1250 -*- | ||
| + | import serial | ||
| + | import logging | ||
| + | import sys | ||
| + | import os | ||
| + | |||
| + | |||
| + | def to_hex_word(a): | ||
| + | '''encodes a decimal number hexadecimally on two bytes''' | ||
| + | return a.to_bytes(2,byteorder=sys.byteorder) | ||
| + | |||
| + | class SerialPortMy(object): | ||
| + | def __init__(self, port_name): | ||
| + | import serial | ||
| + | try: | ||
| + | self.port = serial.Serial( | ||
| + | port=port_name, | ||
| + | baudrate=9600, | ||
| + | bytesize=serial.EIGHTBITS, | ||
| + | parity=serial.PARITY_NONE, | ||
| + | stopbits=serial.STOPBITS_ONE, | ||
| + | xonxoff=False | ||
| + | ) | ||
| + | except serial.SerialException as e: | ||
| + | print("Nieprawidłowa nazwa portu lub port zajęty.") | ||
| + | raise e | ||
| + | self.close() | ||
| + | |||
| + | def open(self): | ||
| + | self.port.open() | ||
| + | |||
| + | def close(self): | ||
| + | self.port.close() | ||
| + | |||
| + | def send(self, value): | ||
| + | self.port.write(value) | ||
| + | |||
| + | def blinkSSVEP(self,d, p1, p2): | ||
| + | ''' | ||
| + | d = list of frequencies; | ||
| + | p1:p2 = ratio LED_on_time/LED_off_time | ||
| + | if you want i-th LED to be OFF all the time send d[i] = 0 | ||
| + | if you want i-th LED to be ON all the time send d[i] = -1 | ||
| + | in these two cases p1 and p2 do not matter | ||
| + | ''' | ||
| + | clock = 62500 | ||
| + | factor = float(p1) / float(p1 + p2) | ||
| + | |||
| + | str = (3).to_bytes(1,byteorder=sys.byteorder) # 'SSVEP_RUN' | ||
| + | |||
| + | for i in range(len(d)): | ||
| + | # i-th LED OFF | ||
| + | if d[i] == 0: | ||
| + | str += to_hex_word(0) + to_hex_word(255) | ||
| + | # i-th LED ON | ||
| + | elif d[i] == -1: | ||
| + | str += to_hex_word(255) + to_hex_word(0) | ||
| + | #str = 'S' | ||
| + | # i-th LED blinks d[i] times per second | ||
| + | # p1:p2 = on_time:off_time in one blink | ||
| + | else: | ||
| + | period = clock/d[i] | ||
| + | bright = int((clock/d[i]) * factor) | ||
| + | dark = period - bright | ||
| + | str += to_hex_word(bright) + to_hex_word(dark) | ||
| + | |||
| + | self.send(str) | ||
| + | |||
| + | def blinkP300(self,d): | ||
| + | clock = 62500 | ||
| + | str = (4).to_bytes(1,byteorder=sys.byteorder) # 'P300_RUN' | ||
| + | |||
| + | for i in range(len(d)): | ||
| + | period = int(clock*d[i]/1000.0) | ||
| + | str += to_hex_word(period) | ||
| + | |||
| + | self.send(str) | ||
| + | |||
| + | </source> | ||
| + | <!-- | ||
| + | |||
| + | |||
| + | |||
# -*- coding: cp1250 -*- | # -*- coding: cp1250 -*- | ||
import serial | import serial | ||
| Linia 182: | Linia 270: | ||
self.send(str) | self.send(str) | ||
| + | --> | ||
| − | |||
| Linia 194: | Linia 282: | ||
# Powtórz punkty 1-2, tak aby uzyskać 15 realizacji migania z każdą z częstości. | # Powtórz punkty 1-2, tak aby uzyskać 15 realizacji migania z każdą z częstości. | ||
| − | + | Zarejestrowana liczba realizacji jednej częstości powinna wynosić minimum 30. Zrealizowanie tego w jednej sesji zajęłoby około 50 minut. Jest to uciążliwe dla osoby badanej, dlatego dzielimy eksperyment na dwie sesje po 20 minut — powtarzamy punkt 3 dwukrotnie. | |
===Wykonanie pomiarów=== | ===Wykonanie pomiarów=== | ||
| − | # Nałóż czepek na głowę badanej osoby i umieść w nim następujące elektrody: Fp1, Fp2, Fpz, Cz, P3, Pz, P4, O1, O2 oraz jeśli twój czepek to umożliwia również elektrody P7 i P8. Jako elektrody referencyjne załóż elektrody A1, A2 lub M1 i M2. | + | # Nałóż czepek na głowę badanej osoby i umieść w nim następujące elektrody: Fp1, Fp2, Fpz, Cz, P3, Pz, P4, O1, O2 oraz jeśli twój czepek to umożliwia również elektrody P7 i P8. Jako elektrody referencyjne załóż elektrody A1, A2 lub M1 i M2. Częstość próbkowania: 1024 Hz. |
# Wykonaj eksperyment zgodnie ze schematem podanym w poprzednim paragrafie. | # Wykonaj eksperyment zgodnie ze schematem podanym w poprzednim paragrafie. | ||
| Linia 208: | Linia 296: | ||
#**Widma odpowiadające tej samej częstości stymulacji uśrednij ze sobą. | #**Widma odpowiadające tej samej częstości stymulacji uśrednij ze sobą. | ||
#**Zaprezentuj widma otrzymane przy stymulacjach różnymi częstościami. | #**Zaprezentuj widma otrzymane przy stymulacjach różnymi częstościami. | ||
| − | #**Dla każdej częstości stymulacji wyznacz miarę odpowiedzi SSVEP (amplitudę widma odpowiadającą częstości stymulacji) wraz z 95% przedziałem ufności dla średniej. Można to zrobić np. metodą bootstrap. Dla każdej częstości stymulacji wyznacz także poziom tła na podstawie widm pochodzących ze stymulacji innymi częstościami. Np. dla stymulacji częstością | + | #**Dla każdej częstości stymulacji wyznacz miarę odpowiedzi SSVEP (amplitudę widma odpowiadającą częstości stymulacji) wraz z 95% przedziałem ufności dla średniej. Można to zrobić np. metodą bootstrap. Dla każdej częstości stymulacji wyznacz także poziom tła na podstawie widm pochodzących ze stymulacji innymi częstościami. Np. dla stymulacji częstością 10 Hz poziom tła można wyznaczyć jako 95 centyl ze zbioru wartości widma w częstości 10 Hz dla stymulacji częstościami {4, 7, 13, 16, 20, 25, 30, 35, 40} Hz. |
#**Sporządź wykres odpowiedzi SSVEP od częstości z zaznaczeniem przedziałów ufności i poziomu tła. Znajdź częstości, dla których odpowiedź ta była najsilniejsza. | #**Sporządź wykres odpowiedzi SSVEP od częstości z zaznaczeniem przedziałów ufności i poziomu tła. Znajdź częstości, dla których odpowiedź ta była najsilniejsza. | ||
#* Sposób II: | #* Sposób II: | ||
| Linia 279: | Linia 367: | ||
Ω(''t'') — częstość chwilowa sygnału ''x''(''t''),<br> | Ω(''t'') — częstość chwilowa sygnału ''x''(''t''),<br> | ||
| − | Do klasy sygnałów, które mogą być reprezentowane w postaci drgania uogólnionego, należą m.in. wszystkie sygnały o ograniczonej energii i ograniczonej mocy średniej przedziałami ciągłe i bez składowej stałej (tzw. sygnały przestrzeni < | + | Do klasy sygnałów, które mogą być reprezentowane w postaci drgania uogólnionego, należą m.in. wszystkie sygnały o ograniczonej energii i ograniczonej mocy średniej przedziałami ciągłe i bez składowej stałej (tzw. sygnały przestrzeni ''L''<sup>2</sup>). |
| − | W celu przedstawienia sygnału | + | W celu przedstawienia sygnału ''x''(''t'') jako drgania uogólnionego należy wpierw wyznaczyć jego ''sygnał analityczny'' ''z''(''t''), który zdefiniowany jest w następujący sposób: |
| − | + | ''z''(''t'') = ''x''(''t'') + ''ix''<sub>H</sub>(''t'') | |
gdzie: <br> | gdzie: <br> | ||
<math>i=\sqrt{-1}</math><br> | <math>i=\sqrt{-1}</math><br> | ||
| − | < | + | ''x''<sub>H</sub>(''t'') — transformata Hilberta sygnału ''x''(''t'').<br> |
| − | Transformatę Hilberta < | + | Transformatę Hilberta ''x''<sub>H</sub>(''t'') sygnału ''x''(''t'') i transformatę do niej odwrotną definiujemy jak poniżej:<br> |
<math> | <math> | ||
x_H(t) = \frac{1}{\pi}\int_{-\infty}^{\infty} \frac{x(\tau)}{t - \tau}d\tau | x_H(t) = \frac{1}{\pi}\int_{-\infty}^{\infty} \frac{x(\tau)}{t - \tau}d\tau | ||
| Linia 301: | Linia 389: | ||
Widmo sygnału analitycznego odpowiadającego sygnałowi rzeczywistemu jest zerowe | Widmo sygnału analitycznego odpowiadającego sygnałowi rzeczywistemu jest zerowe | ||
dla ujemnych częstości, zaś dla dodatnich częstości ma podwojoną amplitudę: | dla ujemnych częstości, zaś dla dodatnich częstości ma podwojoną amplitudę: | ||
| − | < | + | ''x''<sub>''a''</sub> = ''F''<sup>−1</sup>(''F''(''x'')·2''U'') |
gdzie ''F'' — transformacja Fouriera, a ''U'' funkcja schodkowa. | gdzie ''F'' — transformacja Fouriera, a ''U'' funkcja schodkowa. | ||
Metoda ta zaimplementowana jest w funkcji <tt>scipy.signal.hilbert</tt> | Metoda ta zaimplementowana jest w funkcji <tt>scipy.signal.hilbert</tt> | ||
| Linia 333: | Linia 421: | ||
Porównując powyższy wzór ze wzorem na funkcję harmoniczną: | Porównując powyższy wzór ze wzorem na funkcję harmoniczną: | ||
| − | <math>x(t) = A \sin(\ | + | <math>x(t) = A \sin(\omega_0 t + \varphi_0)</math> |
widzimy, że sygnały nieharmoniczne charakteryzują się zmienną w czasie amplitudą i częstością oraz nie mają określonej fazy początkowej. Ten ostatni parametr jednak również może być wyznaczony, pod warunkiem iż określimy go względem pewnej stałej w czasie częstości ω<sub>0</sub>(''t''): | widzimy, że sygnały nieharmoniczne charakteryzują się zmienną w czasie amplitudą i częstością oraz nie mają określonej fazy początkowej. Ten ostatni parametr jednak również może być wyznaczony, pod warunkiem iż określimy go względem pewnej stałej w czasie częstości ω<sub>0</sub>(''t''): | ||
Wersja z 17:10, 13 kwi 2021
Pracownia EEG / SSVEP
Spis treści
Wstęp
Potencjały wywołane stanu ustalonego (ang. Steady State Evoked Potentials, SSEP)
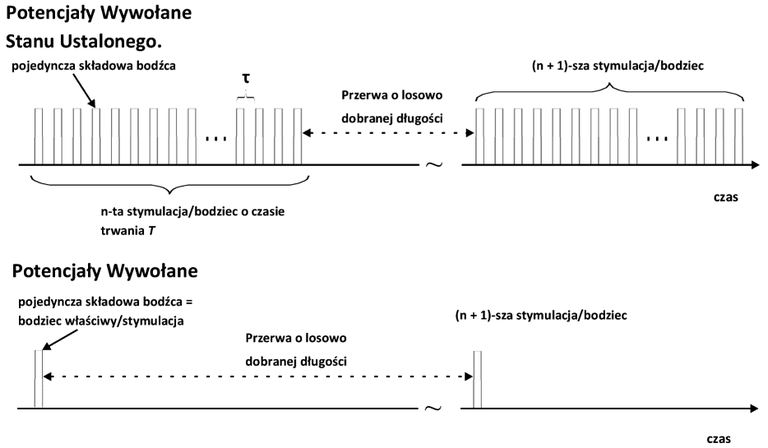
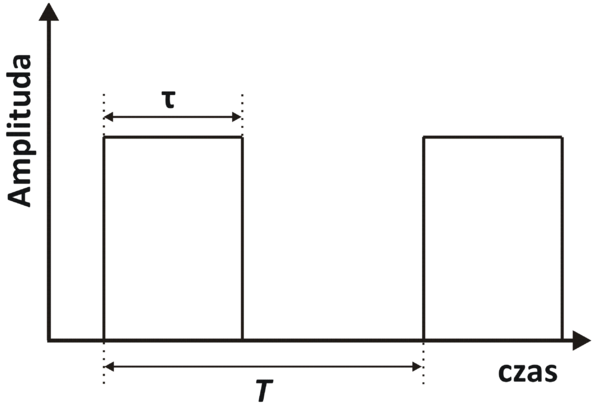
Potencjały wywołane EEG, które mierzyliśmy na poprzednich zajęciach, są śladami reakcji mózgu na pewne specyficzne bodźce. Jak pamiętamy, były to podawane w pewnych odstępach czasu (zwykle około 1 s), krótkotrwałe (~20 ms) błyski światła. W trakcie bieżących zajęć będziemy kontynuowali pomiar czynności elektrycznej mózgu w trakcie oddziaływania na badanego pewnymi bodźcami, jednakże przebieg stymulacji zostanie zmieniony. W tym eksperymencie bodźcem będzie seria powtarzających się w sposób ściśle periodyczny błysków światła (rys. 1). Bodźce o takim przebiegu mogą mieć również postać krótkotrwałych dźwięków (np. trzasków), czy też impulsów mechanicznych (np. rytmiczny nacisk na skórę). Ślad elektrycznej odpowiedzi mózgu na szybko powtarzające się bodźce nazywamy potencjałami wywołanymi stanu ustalonego (ang. Steady State Evoked Potentials, SSEP). W zależności od modalności bodźca (czyli zmysłu, który jest poddawany stymulacji) wyróżniamy:
- wzrokowe potencjały wywołane stanu ustalonego (ang. Steady State Visual Evoked Potentials, SSVEP), w przypadku gdy stymulacja odbywa się za pomocą fali świetlnej (Silberstein, 1995; Vialatte, 2010).
- słuchowe potencjały stanu ustalonego (ang. Auditory Steady State Evoked Response, ASSR), w przypadku gdy stymulacja odbywa się za pomocą fali dźwiękowej.
- czuciowe potencjały wywołane stanu ustalonego (ang. Steady-State Somatosensory Evoked Potentials, SSSEP), wywoływane przy pomocy bodźców mechanicznych.
W języku polskim brakuje zwrotów, za pomocą których można prawidłowo scharakteryzować niektóre parametry bodźców wywołujących odpowiedź SSEP. W związku z tym, na potrzeby niniejszych ćwiczeń zostanie wprowadzona następująca nomenklatura:
- składowa bodźca — przebieg bodźca w jednym okresie stymulacji, np. pojedynczy, krótkotrwały błysk światła, dźwięk lub impuls mechaniczny (patrz rys. 1),
- bodziec/stymulacja/pobudzenie — jest to ciąg o czasie trwania T, złożony z kolejnych występujących po sobie składowych, powtarzających się co okres τ (patrz rys. 1).
Charakterystyczną cechą zjawiska SSEP jest wzrost mocy sygnału EEG w częstości, z którą powtarzane są składowe bodźca. Np. jeśli błysk światła występuje co τ=100 ms, możemy oczekiwać wzrostu mocy elektrycznej aktywności mózgu dla częstości 10 Hz oraz niejednokrotnie dla jej harmonicznych. Moc sygnału ulega dodatkowemu zwiększeniu, jeśli badana osoba koncentruje silnie swoją uwagę na bodźcu. Cecha ta wykorzystywana jest m. in. do budowania tzw. interfejsów mózg komputer, czyli systemów, umożliwiających człowiekowi komunikację z komputerem bez pośrednictwa mięśni.
Modulacja
Analizując od strony fizycznej przebieg bodźców wywołujących zjawisko SSEP możemy zauważyć, iż mamy do czynienia z procesem modulacji sygnału, czyli chwilową zmianą jego parametrów. Niezależnie od tego, który z tych parametrów ulega zmianie, w procesie modulacji wyróżniamy dwa podstawowe sygnały — sygnał nośny oraz sygnał modulujący [[1]]. W technice radiowej czy telewizyjnej sygnałem nośnym są fale elektromagnetyczne. W przypadku wywoływania zjawiska SSVEP sygnałem nośnym też jest fala elektromagnetyczna, ale o długości z zakresu światła widzialnego. Z kolei zjawisko ASSR powstaje na skutek stymulacji, w której falą nośną jest fala dźwiękowa o częstości od kilkuset do kilku tysięcy Hz. Sygnał, który zmienia parametry fali nośnej nazywamy sygnałem modulującym. Przebieg sygnału modulującego może mieć różny charakter, jednakże najczęściej stosowane są sygnały o kształcie sinusoidalnym lub prostokątnym. W przypadku modulacji za pomocą sygnału sinusoidalnego zmianie może ulec amplituda, częstość lub faza sygnału nośnego. Mówimy wtedy odpowiednio o modulacji amplitudowej (ang. Amplitude Modulation, AM), częstościowej (ang. Frequency Modulation, FM) lub fazowej (ang. Phase Modulation, PM). Modulacja FM i PM nie jest stosowana do wywoływania zjawiska SSEP, natomiast modulację AM wykorzystuje się do pomiaru ASSR, w związku z czym zostanie opisana szerzej.
Modulacja amplitudowa sygnałem sinusoidalnym
Niech: [math]x(t) = A \sin(\Omega t)[/math] będzie sygnałem nośnym o częstości Ω i amplitudzie A, zaś [math]y(t) = B \sin(\omega t+ \varphi)[/math] będzie sygnałem modulującym o częstości ω, amplitudzie B i fazie początkowej φ. Sygnałem zmodulowanym amplitudowo nazywamy następujący sygnał: [math]z(t) = A \sin(\Omega t) + B \sin(\omega t + \varphi)\cdot \sin(\Omega t)[/math] Korzystając ze wzorów trygonometrycznych, powyższy wzór można zapisać w postaci: [math]z(t) = A \sin(\Omega t) + B \frac{\cos((\Omega - \omega) t+\varphi)}{2} - B \frac{\cos((\Omega + \omega) t+\varphi)}{2}[/math] Jak można zauważyć, energia sygnału zmodulowanego amplitudowo skupiona jest wokół trzech częstości:
- częstości nośnej [math]f_0=\Omega[/math],
- częstości [math]f_1=\Omega - \omega[/math] i [math]f_2=\Omega + \omega[/math].
Część widma sygnału zmodulowanego skupioną w częstościach [math]f_1[/math] i [math]f_2[/math] nazywamy wstęgami bocznymi.
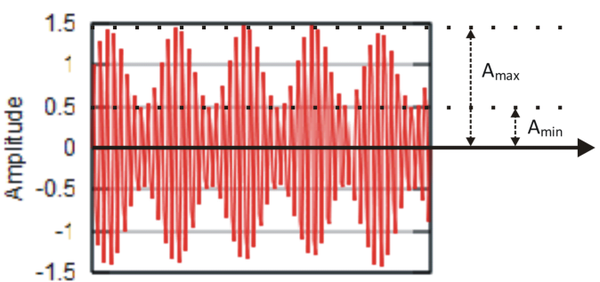
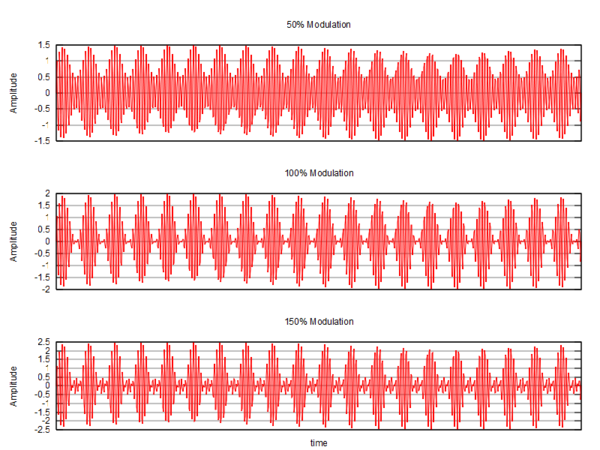
Modulację amplitudową można scharakteryzować za pomocą tzw. współczynnika głębokości modulacji, zdefiniowanego w następujący sposób (patrz rys. 2): [math]m=\frac{A_{max}-A_{min}}{A_{max}+A_{min}}[/math] Powyższy wzór można w prosty sposób przekształcić do następującej postaci: [math]m=\frac{A_{max}-A_{min}}{A_{max}+A_{min}} = \frac{B}{A}[/math] Głębokość modulacji może osiągać dowolne wartości dodatnie, jednakże w praktyce współczynnik ten powinien zawierać się w granicy pomiędzy 0 a 1 (bądź od 0 do 100 %). W przypadku gdy głębokość modulacji osiąga wartość wyższą niż 1, sygnał zostaje zniekształcony (patrz rys. 3) i nie ma praktycznego wykorzystania.
Modulacja amplitudowa falą prostokątną
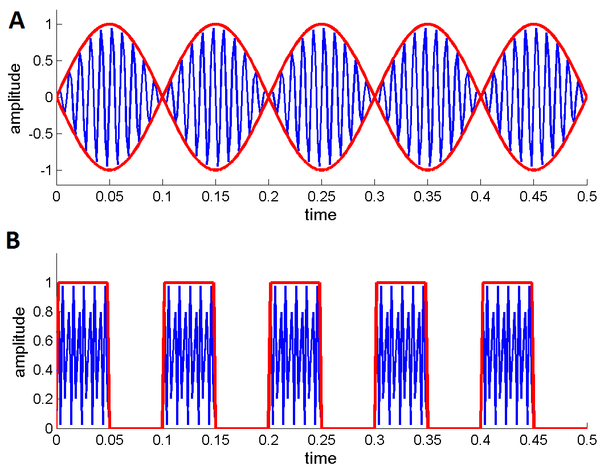
W przypadku wywoływania zjawiska SSEP stosuje się bodźce, w których fala nośna (światło) zostaje zmodulowany sygnałem prostokątnym. Porównanie modulacji amplitudowej sygnałem o przebiegu sinusoidalnym i sygnałem o przebiegu prostokątnym zaprezentowano na rysunku rys. 4. W przypadku modulacji falą prostokątną rozważamy następujące parametry:
- częstość modulacji, która równa jest odwrotności okresu powtarzania się impulsu prostokątnego (na rys. 4 okres ten jest równy T),
- amplitudę modulacji,
- wypełnienie fali, które zdefiniowane jest w następujący sposób:
[math] d = \frac{\tau}{T}[/math]
Fizjologia zjawisk SSEP i SSVEP
SSEP
Potencjały Wywołane Stanu Ustalonego to typ odpowiedzi mózgu na bodziec powtarzany ze stałą częstotliwością. Efektem takiej stymulacji jest pojawienie się w określonych obszarach kory mózgowej częstotliwości korespondującej z częstotliwością podawanego bodźca.
Stawianych jest kilka hipotez, z których trzy starają się tłumaczyć najbardziej podstawowy mechanizm pojawiania się tego zjawiska w mózgu:
- Pierwsza z nich mówi, iż powtarzany z określoną częstością bodziec wywołuje każdorazowo odpowiedź, a ich ciąg znajduje odbicie w rejestrowanym sygnale EEG (Lachowska, 2009; Rance, 2008). Zakłada się tutaj, iż do powstania odpowiedzi konieczne są niższe piętra przetwarzania informacji oraz brak specyficznego obszaru kory lub sieci neuronalnej odpowiedzialnej za obróbkę tego typu bodźców. Argumentów potwierdzających dostarczają tutaj badania na zwierzętach, gdzie rejestrowano SSEP z poszczególnych pięter układu nerwowego (Yoris, 1992; za: Rance, 2008). Słabe strony tej hipotezy ujawniają badania neuroobrazownia, w których rejestruje się aktywność w rejonach niezwiązanych z przetwarzaniem pojedynczego impulsu danej modalności (Pastor, 2003; Reyes, 2004). Sugeruje to, iż istnieje obszar lub sieć neuronów odpowiedzialna za przetwarzanie tego typu bodźca i jest ona aktywowana wraz z rejonami kory, których zadaniem jest odbiór i interpretacja danych dostarczanych przez poszczególne zmysły.
- Druga z tych hipotez mówi, iż w trakcie stymulacji dochodzi do synchronizacji odpalania potencjałów czynnościowych przez neurony, co przejawia się zwiększeniem siły odpowiedzi w danej częstotliwości na tle aktywności spontanicznej mózgu (Moratti, 2007).
- Trzecia hipoteza zakłada, że obserwowany w sygnale potencjał jest związany ze wzrostem amplitudy odpowiedzi aktywowanych neuronów (Nikulin, 2007; za: Vialatte, 2010).
Żadne ze wspomnianych badań nie zostało przeprowadzone z myślą o pokazaniu genezy indukowania potencjału SSEP, lecz dotyczyły wybranych bodźców i zagadnień związanych z ich charakterystyką odpowiedzi. Na podstawie zebranych dotychczas danych trudno orzec o słuszności którejś z wyżej wymienionych hipotez.
SSVEP
Wzrokowe Potencjały Wywołane Stanu Ustalonego (SSVEP) powstają pod wpływem stymulacji bodźcem świetlnym powtarzanym ze stałą częstością. W trakcie stymulacji w sygnale EEG obserwowany jest wzrost mocy w częstościach związanych z częstością pulsującego światła. Charakterystyczne dla potencjałów SSVEP jest występowanie zarówno częstości podstawowej — analogicznej jak częstość stymulatora — jak i pierwszej i drugiej harmonicznej oraz subharmonicznych (Hermann, 2001; Pastor, 2003; Vialatte, 2008). W pracy (Regan, 1989; za: Silberstein, 1995) wyróżniono szereg komponentów, które są charakterystyczne dla SSVEP. W zależności od częstości stymulacji zaobserwowana została zmienność w kształcie oraz latencji charakterystycznych załamków SSVEP. Dla częstości wysokich od 25 do 60 Hz — charakterystyczna składowa fali pojawia się do 30 do 60 ms po bodźcu i odznacza się małą zmiennością międzyosobniczą. Wcześniejsze załamki (ok. 10 ms) są obserwowane, ich latencja wydaje się być zależna od wieku osoby. Przedział częstości niskich od 15 do 25 Hz — odznacza się obecnością swoistego komponentu od około 85 do 120 ms po bodźcu. W tym przypadku wariancja wewnątrz grupy jest większa w porównaniu do częstości wysokich. Najtrudniej trafnie wyodrębnić charakterystyczne składowe dla odpowiedzi na niskie częstotliwości stymulatora. Latencja w tym przypadku waha się od 135 do 350 ms.
Przestrzenna lokalizacja generatorów SSVEP.
Pomimo, iż powstanie SSVEP jest nierozerwalnie związane z okolicami wzrokowymi kory mózgowej (Bianciardi, 2009; Pastor, 2003; Silberstein, 1995), jego występowanie mapuje się również w innych rejonach mózgu. Wytyczenie obszarów odpowiedzialnych za generowanie potencjału zostało podjęte przy pomocy różnych metod mierzących aktywność mózgu. Oprócz EEG wykorzystano PET (Pastor, 2003), MEG (Fewcett, 2004; za: Vialatte, 2010) i fMRI (Bayram, 2011; Bianciardi, 2009; Parkes, 2003). Wyniki tych badań nie dają jednoznacznej odpowiedzi na stawiane pytanie, ale można na ich podstawie wskazać na kilka struktur, których aktywność wydaje się być znacząca i każdorazowo rejestrowana. Głównym obszarem generującym oscylujący potencjał jest pierwszorzędowa kora wzrokowa V1. Jej aktywacja zaznacza się w momencie stymulacji bodźcami świetlnymi bez względu na przedział częstotliwości i ich parametry. Różne badania donoszą natomiast o dodatkowych obszarach mających swój udział w generowaniu odpowiedzi mózgowej na pulsujący bodziec (V5, (Fawcett, 2004; za: Vialatte, 2010) kora czołowa i skroniowa, V2 (Sriniviasan, 2006, 2007; za: Vialatte, 2010). Badanie wykonane za pomocą PET (Pastor, 2003) przybliżyło szczegóły rozkładu aktywacji ośrodków korowych podczas generowania SSVEP. Oprócz zlokalizowania jego występowania w obszarach płatów potylicznych, skroniowych oraz ciemieniowych, dzięki użyciu różnych znaczników nakreślone zostały granice aktywności kory w zależności od częstotliwości stymulatora. Dla niskich częstotliwości (w badaniu reprezentowanych przez 5Hz) obserwuje się aktywność w polach Brodmanna (BA) 17 i 18 oraz w lewej półkuli móżdżku, dla częstości średnich pobudzony był obszar pierwszorzędowej kory wzrokowej oraz kory asocjacyjnej (BA 17 i 18). Nieco odmienne rezultaty otrzymano dla częstości 40 Hz, która pobudzała tylną część V1 oraz korę asocjacyjną prawej półkuli. Taki rozkład aktywacji przy wyżej wymienionych częstościach może być związany z funkcjonalny podziałem V1 — obszar przedni pobudzany przez niskie i średnie częstości (<30 Hz) jest odpowiedzialny za widzenie peryferyjne, wtedy pobudzona była dość duża powierzchnia kory. 40 Hz aktywuje natomiast rejony odpowiedzialne za widzenie centralne, stąd mały, ograniczony do wybranych kolumn, obszar pobudzenia. Rejony, którym przypisane zostało generowanie SSVEP, nie ograniczały się do okolic wzrokowych. Oprócz okolicy V1 wymieniany jest również obszar V5, odpowiedzialny za detekcje ruchu, mający bezpośrednie połączenia z V1, inne okolice wzrokowe oraz kora czołowa. Niskoczęstotliwościowe SSVEP zauważano również na poziomie struktur śródmózgowia — w ciele kolankowatym bocznym, co zaowocowało hipotezą o podkorowej proweniencji takich potencjałów.
Tak zróżnicowany obraz aktywności wywoływanych przez różne częstości SSVEP może wynikać z różnych funkcjonalnych i anatomicznych właściwości poszczególnych regionów. W układzie wzrokowym człowieka rozpoznane zostały 3 odmienne drogi przetwarzania informacji odpowiadającej tej modalności (Chatterjee, 2003; za: Vialatte, 2010; Gazzaniga, 2004; za: Vialatte, 2010). Każda z nich związana jest z innym typem czopków: odpowiadającymi na krótkie, średnie o długie fale. Droga Parvocellular (PC) mająca swój początek w midget retinal ganglion cells (RGCs) przetwarza informację o kolorze, kształcie oraz przestrzennym kontraście. Jest wyczulona szczególnie na przenoszenie informacji o kolorze czerwonym i zielonym, która jest przekazywana z czopków L i M (long- i mediumwave). Z kolei droga Magnocellular (MC), będąca dużo szybszym kanałem, bierze swój początek w parasol retinal ganglion cells. Odpowiada ona za dostarczenie informacji o ruchu i głębi. Również korzysta z informacji z czopków M i L. Ostatnio odkryto trzeci z kanałów — drogę Koniocellular (KC) zaczynającą się w bistratisfied retina ganglion cells, odpowiadający za percepcję kolorów błękitnego oraz żółtego. Niektórzy badacze wysuwają hipotezę, że wyłącznie tan kanał dostarcza informacji o kolorach, podczas gdy kanał PC odpowiada za dobrą rozdzielczość percepowanej informacji (Foxe, 2008; za: Vialatte, 2010; Chatterjee, 2003; za: Vialatte, 2010). Droga MC tworzy tzw. kanał brzuszny obróbki informacji a szlak KC i PC — kanały grzbietowe. Na pytanie o zależność pomiędzy rodzajem kanału a SSVEP żaden z badaczy nie udzielił wyczerpującej odpowiedzi. Podejrzewa się, iż w zależności od miejsca generowania SSVEP siła odpowiedzi będzie zależna od wyglądu bodźca. Możliwe, iż obszary kanału grzbietowego będą odznaczały się predylekcją do bodźców jednobarwnych, niejaskrawych, o dość dużych rozmiarach oraz migających z wysoką częstotliwością. Drogi KC i PC natomiast będą generować mocne SSVEP, jeżeli będą pobudzane przez kolorowe kontrastowe bodźce o małych rozmiarach w niskiej częstości. Odmienną hipotezę zaproponował McKeefry (McKeefry, 1996, za: Vialatte, 2010), który skojarzył drogi obróbki informacji z rodzajem komórek. W ten sposób upatruje on powstawanie pierwszej harmonicznej dzięki aktywności komórek tonicznych i drogi PC, a drugiej harmonicznej — dzięki komórkom fazowym i szlakowi MC. W świetle tych hipotez należałoby się spodziewać, iż siła odpowiedzi będzie zależeć od wyglądu stosowanego bodźca, lokalizacji rejestracji sygnału na głowie oraz częstości.
Ćwiczenia eksperymentalne
Do rejestracji zjawiska SSVEP wykorzystamy ten sam zestaw eksperymentalny co w przypadku badania Potencjałów Wywołanych. Poniżej przypominamy schemat komunikacji w języku Python pomiędzy komputerem a mikrokontrolerem sterującym wyświetlaniem bodźców. Czcionką pogrubioną wyszczególniono fragment kodu, który jest niezbędny do wytworzenia szybko powtarzających się bodźców świetlnych.
- Po podłączeniu przejściówki USB/RS232 do komputera mikrokontrolera sprawdź jaki plik w katalogu /dev został utworzony i przydzielony do urządzenia.
- poproś osobę prowadzącą aby dodała cię do grupy plugdev
sudo usermod -a -G plugdev userName
- Zaimportuj bibliotekę do komunikacji z mikrokontrolerem:
- import SerialPort as SP
- Otwórz plik powiązany z urządzeniem zewnętrznym:
- sp = SP.SerialPort(nazwa_pliku)
- sp.open()
gdzie przykładowa nazwa pliku wynosi /dev/ttyUSB0.
- Po włączeniu zasilania mikrokontrolera, diody podłączone do niego i wykorzystywane w eksperymencie z potencjałami wywołanymi będą zapalone. Następujące polecenie zgasi obydwie diody:
- sp.blinkSSVEP([0, 0],1,1)
- Wydanie poniższego polecenia spowoduje, iż mikrokontroler będzie generował sygnał prostokątny zapalający i gaszący podłączoną do niego diodę numer 1, z częstością f Hz i współczynnikiem wypełnieniem równym [math]\frac{x}{x+y}[/math], zaś dioda numer 2 pozostanie zgaszona:
- sp.blinkSSVEP([f, 0],x,y)
Jednocześnie, moment pojawienia się każdej składowej bodźca (każdego impulsu świetlnego) zostanie przesłany na na 5-stykowe wejście AUX mikrokontrolera. Przykładowo jeśli chcemy aby dioda migała z częstością 10 Hz i współczynnikiem wypełnienia 0,5 wydajemy następujące polecenie:
- sp.blinkSSVEP([10, 0],1,1)
- Jeśli chcemy zakończyć komunikację z mikrokontrolerem piszemy:
- sp.close()
Kod biblioteki do komunikacji z mikrokontrolerem:
# -*- coding: cp1250 -*-
import serial
import logging
import sys
import os
def to_hex_word(a):
'''encodes a decimal number hexadecimally on two bytes'''
return a.to_bytes(2,byteorder=sys.byteorder)
class SerialPortMy(object):
def __init__(self, port_name):
import serial
try:
self.port = serial.Serial(
port=port_name,
baudrate=9600,
bytesize=serial.EIGHTBITS,
parity=serial.PARITY_NONE,
stopbits=serial.STOPBITS_ONE,
xonxoff=False
)
except serial.SerialException as e:
print("Nieprawidłowa nazwa portu lub port zajęty.")
raise e
self.close()
def open(self):
self.port.open()
def close(self):
self.port.close()
def send(self, value):
self.port.write(value)
def blinkSSVEP(self,d, p1, p2):
'''
d = list of frequencies;
p1:p2 = ratio LED_on_time/LED_off_time
if you want i-th LED to be OFF all the time send d[i] = 0
if you want i-th LED to be ON all the time send d[i] = -1
in these two cases p1 and p2 do not matter
'''
clock = 62500
factor = float(p1) / float(p1 + p2)
str = (3).to_bytes(1,byteorder=sys.byteorder) # 'SSVEP_RUN'
for i in range(len(d)):
# i-th LED OFF
if d[i] == 0:
str += to_hex_word(0) + to_hex_word(255)
# i-th LED ON
elif d[i] == -1:
str += to_hex_word(255) + to_hex_word(0)
#str = 'S'
# i-th LED blinks d[i] times per second
# p1:p2 = on_time:off_time in one blink
else:
period = clock/d[i]
bright = int((clock/d[i]) * factor)
dark = period - bright
str += to_hex_word(bright) + to_hex_word(dark)
self.send(str)
def blinkP300(self,d):
clock = 62500
str = (4).to_bytes(1,byteorder=sys.byteorder) # 'P300_RUN'
for i in range(len(d)):
period = int(clock*d[i]/1000.0)
str += to_hex_word(period)
self.send(str)
Ćwiczenie I: Wykreślenie krzywej odpowiedzi dla badanej osoby.
W ogólności siła odpowiedź SSVEP maleje wraz ze wzrostem częstości, jednak każda osoba ma indywidualne preferencje co do częstości, z którymi powinien migać bodziec. Celem eksperymentu jest znalezienie zbioru częstości, dla których badana osoba reaguje najsilniej. Aby przeprowadzić eksperyment, wykonaj następujące kroki:
Przygotowanie programu do sterowania eksperymentem
Napisz program komputerowy, który będzie:
- wybierał losowo z jednakowym prawdopodobieństwem częstość ze zbioru częstości {4, 7, 10, 13, 16, 20, 25, 30, 35, 40} Hz
- uruchamiał miganie jednej diody podłączonej do zestawu eksperymentalnego z częstościami wybraną częstością na czas 5 sek (wypełnienie 50%). Po 5-sekundowym okresie migania, powinna się pojawić przerwa o losowym czasie trwania od 3 do 7 sekund. Momenty pojawiania się poszczególnych częstości rejestruj w pliku. Będzie to potrzebne w dalszej części ćwiczenia do powiązania triggera z częstością stymulacji.
- Powtórz punkty 1-2, tak aby uzyskać 15 realizacji migania z każdą z częstości.
Zarejestrowana liczba realizacji jednej częstości powinna wynosić minimum 30. Zrealizowanie tego w jednej sesji zajęłoby około 50 minut. Jest to uciążliwe dla osoby badanej, dlatego dzielimy eksperyment na dwie sesje po 20 minut — powtarzamy punkt 3 dwukrotnie.
Wykonanie pomiarów
- Nałóż czepek na głowę badanej osoby i umieść w nim następujące elektrody: Fp1, Fp2, Fpz, Cz, P3, Pz, P4, O1, O2 oraz jeśli twój czepek to umożliwia również elektrody P7 i P8. Jako elektrody referencyjne załóż elektrody A1, A2 lub M1 i M2. Częstość próbkowania: 1024 Hz.
- Wykonaj eksperyment zgodnie ze schematem podanym w poprzednim paragrafie.
Analiza danych
- Przefiltruj sygnały EEG w paśmie 1-45 Hz za pomocą procedury filtfilt.
- Na podstawie sygnału trigger oraz danych zapisanych w pliku wyodrębnij sygnały EEG zarejestrowane w trakcie stymulacji z odpowiednimi częstościami.
- Przeanalizuj dane na trzy sposoby:
- Sposób I:
- Dla każdej realizacji wyestymuj przy pomocy transformaty Fouriera widmo amplitudowe sygnału EEG.
- Widma odpowiadające tej samej częstości stymulacji uśrednij ze sobą.
- Zaprezentuj widma otrzymane przy stymulacjach różnymi częstościami.
- Dla każdej częstości stymulacji wyznacz miarę odpowiedzi SSVEP (amplitudę widma odpowiadającą częstości stymulacji) wraz z 95% przedziałem ufności dla średniej. Można to zrobić np. metodą bootstrap. Dla każdej częstości stymulacji wyznacz także poziom tła na podstawie widm pochodzących ze stymulacji innymi częstościami. Np. dla stymulacji częstością 10 Hz poziom tła można wyznaczyć jako 95 centyl ze zbioru wartości widma w częstości 10 Hz dla stymulacji częstościami {4, 7, 13, 16, 20, 25, 30, 35, 40} Hz.
- Sporządź wykres odpowiedzi SSVEP od częstości z zaznaczeniem przedziałów ufności i poziomu tła. Znajdź częstości, dla których odpowiedź ta była najsilniejsza.
- Sposób II:
- Uśrednij sygnały odpowiadające stymulacji tą samą częstością.
- Obejrzyj uśrednione sygnały. (Zaprezentuj je).
- Wyestymuj przy pomocy transformaty Fouriera widmo amplitudowe średniego sygnału EEG.
- Dla każdej częstości stymulacji wyznacz miarę odpowiedzi SSVEP wraz z 95% przedziałem ufności dla średniej. Dla każdej częstości stymulacji wyznacz także poziom tła.
- Sporządź wykres odpowiedzi SSVEP od częstości. Znajdź częstości, dla których odpowiedź ta była najsilniejsza.
- Sposób III:
- Dla każdego powtórzenia o danej częstości oblicz transformatę Fouriera
- Uśrednij zespolone transformaty
- Wyestymuj widmo amplitudowe z uśrednionej transformaty Fouriera (oblicz jej moduł), wraz z 95% przedziałem ufności dla średniej. Dla każdej częstości stymulacji wyznacz także poziom tła.
- Sporządź wykres odpowiedzi SSVEP od częstości. Znajdź częstości, dla których odpowiedź ta była najsilniejsza.
- Porównaj opisane powyżej trzy metody. Przy porównaniu uwzględnij:
- Średnie widma przy stymulacji określoną częstością.
- Uzyskane krzywe odpowiedzi SSVEP i wyestymowane przedziały ufności.
- Odstęp między poziomem odpowiedzi a poziomem tła.
- Czy można wyciągnąć jakieś wnioski na temat związku między fazą bodźca a fazą odpowiedzi?
- Sposób I:
Ćwiczenie dla chętnych
Proszę zaimplementować funkcję generujacą znaczniki (tagi) dla programu SVAROG. Tagi te powinny wskazywać momenty rozpoczęcia błyskania diody z określoną częstością. Następnie proszę uśrednić sygnały, korzystając z narzędzia do uśredniania potencjałów w SVAROGU (zakładka Tools->Average evoked potentials), względem tak wskazanych momentów czasu.
Aby wytworzyć tagi dla SVAROGA z poziomu pythona, można wzorować się na następującym kodzie:
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# Author:
# Mateusz Kruszyński <mateusz.kruszynski@titanis.pl>
from obci.analysis.obci_signal_processing.tags import tags_file_writer as tags_writer
from obci.analysis.obci_signal_processing.tags import tag_utils
def main():
writer = tags_writer.TagsFileWriter('./nic.obci.tag')
for i in range(5):
tag = tag_utils.pack_tag_to_dict(float(i), float(i)+0.1, 'tekst', {})
writer.tag_received(tag)
writer.finish_saving(0.0)
if __name__ == "__main__":
main()
Gdzie:
- writer - obiekt, który będzie zapisywał tagi do pliku zdefiniowanego w nim (w tym przykładzie "nic.obci.tag"),
- tag_utils.pack_tag_to_dict - to tworzy tag, pierwsza liczba to poczatek druga koniec tagu, pozniej jest tekst do taga i dodatkowe opcje, które można sprawdzić w helpie,
- writer.tag_received(tag) - to przekazuje taga do writera,
- writer.finish_saving - kończy operacje zapisywania jako argument podany jest czas pierwszej próbki
Koncepcja drgania uogólnionego. Transformata Hilberta
Wstęp
Sygnałem najczęściej występującym w przyrodzie oraz najczęściej stosowanym w technice jest sygnał harmoniczny o postaci:
x(t) = Asin(ωt+φ0),
gdzie:
t — chwila czasu
A — amplituda sygnału,
ω — częstość sygnału,
φ0 — faza początkowa sygnału.
Okazuje się, że istnieje szeroka klasa sygnałów rzeczywistych, które można przedstawić w postaci tzw. drgania uogólnionego: x(t) = A(t)sin(Ω(t) · t)
gdzie:
t — chwila czasu
A(t) — amplituda chwilowa sygnału x(t) (jego obwiednia),
Ω(t) — częstość chwilowa sygnału x(t),
Do klasy sygnałów, które mogą być reprezentowane w postaci drgania uogólnionego, należą m.in. wszystkie sygnały o ograniczonej energii i ograniczonej mocy średniej przedziałami ciągłe i bez składowej stałej (tzw. sygnały przestrzeni L2). W celu przedstawienia sygnału x(t) jako drgania uogólnionego należy wpierw wyznaczyć jego sygnał analityczny z(t), który zdefiniowany jest w następujący sposób:
z(t) = x(t) + ixH(t)
gdzie:
[math]i=\sqrt{-1}[/math]
xH(t) — transformata Hilberta sygnału x(t).
Transformatę Hilberta xH(t) sygnału x(t) i transformatę do niej odwrotną definiujemy jak poniżej:
[math]
x_H(t) = \frac{1}{\pi}\int_{-\infty}^{\infty} \frac{x(\tau)}{t - \tau}d\tau
[/math]
[math]
x(t) = -\frac{1}{\pi}\int_{-\infty}^{\infty} \frac{x_H(\tau)}{t - \tau}d\tau
[/math]
Uwaga praktyczna: do wyznaczania sygnału analitycznego korzysta się z jego następującej własności: Widmo sygnału analitycznego odpowiadającego sygnałowi rzeczywistemu jest zerowe dla ujemnych częstości, zaś dla dodatnich częstości ma podwojoną amplitudę: xa = F−1(F(x)·2U) gdzie F — transformacja Fouriera, a U funkcja schodkowa. Metoda ta zaimplementowana jest w funkcji scipy.signal.hilbert
Jak można zauważyć, sygnał analityczny jest funkcją zespoloną, w związku z czym można go przedstawić w postaci:
[math]
z(t) = \left|z(t)\right|e^{i\varphi(t)}
[/math]
gdzie (patrz równanie (3)):
[math]
\begin{array}{l}
\left|z(t)\right| = \sqrt{x^2(t) + x^2_H(t)} \\
\\
\varphi(t) = \mathrm{arc\,tg}(\frac{x_H(t)}{x(t)})
\end{array}
[/math]
Wielkości te służą do wyznaczania chwilowej fazy φ (wzór powyżej), chwilowej amplitudy A (obwiedni) oraz chwilowej częstości Ω sygnału [math]x(t)[/math]:
[math] \begin{array}{l} A(t)=\left|z(t)\right| \\ \\ \Omega(t) = \frac{d\varphi(t)}{dt} \end{array} [/math]
co umożliwia przedstawienie sygnału x(t) w postaci drgania uogólnionego: [math]x(t) = A(t) \sin(\Omega(t)\cdot t)[/math]
Porównując powyższy wzór ze wzorem na funkcję harmoniczną: [math]x(t) = A \sin(\omega_0 t + \varphi_0)[/math]
widzimy, że sygnały nieharmoniczne charakteryzują się zmienną w czasie amplitudą i częstością oraz nie mają określonej fazy początkowej. Ten ostatni parametr jednak również może być wyznaczony, pod warunkiem iż określimy go względem pewnej stałej w czasie częstości ω0(t):
[math]\varphi(t)=\omega_0\cdot t + \varphi_0(t)[/math]
gdzie:
[math]\varphi_0(t)[/math] — faza chwilowa sygnału [math]x(t)[/math].
Faza chwilowa jest zatem zdefiniowana jednoznacznie, ale tylko względem określonej częstości [math]\omega_0[/math]. W przypadku gdy analizujemy sygnały szerokopasmowe, wyznaczenie fazy chwilowej jest możliwe po przefiltrowaniu sygnału filtrem pasmowo-przepustowym.
Ćwiczenia symulacyjne
Proszę zaimplementować funkcje generujące następujące przebiegi czasowe (oznaczenia: Fs — częstość próbkowania, T — czas trwania w sekundach, analogicznie do tego):
- sinusoida o zadanej częstości f i fazie [math]\phi[/math]: y = sin(f, phi, Fs, T),
- funkcja Gabora o zadanym położeniu szerokości i częstości y = gabor(t0, sigma, omega, Fs, T):
- [math]g_1(t) = \exp\left(-\frac{(t-t_0)^2}{2 \sigma^2}\right)\cdot \cos\left(\omega(t-t_0) \right)[/math].
Ćwiczenie 1
- Wygeneruj 2-sekundowy odcinek sygnału Gabora o pozycji w czasie t0 = 1 s, częstości 16 Hz, skali 0,1 s i częstości próbkowania 128 Hz.
- Wyznacz i narysuj amplitudę chwilową sygnału Gabora.
Ćwiczenie 2
- Wyznacz i narysuj amplitudę chwilową sygnału sinusoidalnego, o częstości 16 Hz i częstości próbkowania 128 Hz.
- Wyznacz i narysuj fazę chwilową sygnału sinusoidalnego, korzystając ze związku:
[math]\varphi(t)=\omega_0\cdot t + \varphi_0(t)[/math]
Ćwiczenie 3
Wygeneruj dwa sygnały sinusoidalne o tej samej częstości 32 Hz i częstości próbkowania 128 Hz, ale różnych fazach początkowych. Pierwszy sygnał powinien mieć fazę początkową równą 0, drugi sygnał sinusoidalny powinien mieć fazę początkową równą π/4. Za pomocą transformaty Hilberta wyznacz różnicę faz symulowanych sygnałów.
Ćwiczenie 4
To ćwiczenie jest ku przestrodze. Wytwórz sygnał będący sumą dwóch sinusoid: jednej o częstości 30 i drugiej o częstości 32 Hz. Wykreśl przebieg sygnału i jego amplitudy chwilowej.
Ćwiczenia na danych pomiarowych
Ćwiczenie 1
W zebranych sygnałach SSVEP wybierz zapisy dla trzech różnych częstości stymulacji (po jednym dla każdej częstości). Do analizy wybierz trzy kanały EEG, dla których sygnał SSVEP jest a) bardzo wyraźny; b) widoczny, ale słabszy; c) w zasadzie niewidoczny. Do analizy wybierz fragmenty od 2 sekund przed rozpoczęciem stymulacji do 2 sekund po jej zakończeniu.
Dla każdej wybranej częstości stymulacji wybrane kanały EEG przefiltruj filtrem wąskopasmowym przepuszczającym częstości skupione wokół tej częstości stymulacji. Do przefiltrowanych sygnałów zastosuj transformację Hilberta, wyznacz amplitudę i częstość chwilową. Wyznacz fazę chwilową dla ω0 równej częstości stymulacji. Wypróbuj dwa sposoby filtrowania: „w jedną stronę” (filter) i „w obie strony” (filtfilt).
Wyrysuj przefiltrowane sygnały wraz z wyliczoną amplitudą chwilową. Do rysunku dodaj wykres sygnału triggera aby widać było początek i koniec stymulacji. Narysuj też wykres zależności częstości chwilowej i fazy chwilowej od czasu.
Bibliografia
- Silberstein, R. (1995). Steady-state visually evoked potentials, brain resonances, and cognitive processes. W: Nunez, P. (red.), Neocortical Dynamics and Human EEG Rhythms (272-303). Oxford University Press, Oxford.
- Vialatte, F., Maurice, M., Dauwels, J. i Cichocki, A. (2010). Steady- state visually evoked potentials: Focus on essential paradigms and future perspectives. Progress in Neurobiology, 90, 418-438.
- Lachowska, M., Morawski, K., Delgado, R. i Niemczyk, K. (2009). Postępy w audiologii. Słuchowe potencjały wywołane stanu ustalonego. Otorynolaryngologia, 8(1), 1-7.
- Rance, G. (red.) (2008). The Auditory Steady-State Response: Generation, Recording and Clinical Application. Plural Publishing, San Diego.
- Scherer, R., Muller-Putz, G. i Pfurtscheller, G. (2009). Flexibility and practicality: Graz Brain-Computer Interface approach. Internationl Review of Neurobiology, 86.
- Pastor, M., Artieda, J., Arbizu,J., Valencia, M. i Masdeu, J. (2003). Human cerebral activation during steady-state visual-evoked responses. Journal of Neuroscience, 23(37), 621-627.
- Moratti, S., Clementz, B., Gao, Y., Ortiz, T. i Keil, A. (2007). Neural mechanisms of evoked oscillations: stability and interaction with transient events. Human Brain Mapping, 28(12), 1318-1333.
- Artykuł o BCI Appliance z prostą funkcją detekcji SSVEP P. J. Durka, R. Kuś, J. Ż̇ygierewicz, M. Michalska, P. Milanowski, M. Łabę̨cki, T. Spustek, D. Laszuk, A. Duszyk, M. Kruszyński. User-centered design of brain-computer interfaces: OpenBCI.pl and BCI Appliance. Bulletin of the Polish Academy of Sciences, vol. 60, No 3, september 2012, pp. 427-433