Analiza sygnałów wielowymiarowych

AS/ Analiza sygnałów wielozmiennych

Stan badanego systemu może być odzwierciedlany zmianami więcej niż jednego sygnału. Do analizy rynku konieczne może być uwzględnienie zmian wartości wielu spółek i jednocześnie innych wskaźników gospodarczych, na potrzeby badania czynności elektrycznej mózgu (EEG) czy serca (EKG) zapisujemy przebiegi potencjału z wielu elektrod umieszczonych w różnych miejscach na głowie czy klatce piersiowej. Sygnałem N-wymiarowym nazwiemy przypisanie każdej chwili czasu [math]t[/math] wektora wartości [math]\vec{s}=\{s_1, s_2 \dots s_N\}[/math], opisującego wartości przyjmowane przez każdy z mierzonych sygnałów [math]s_1(t), s_2(t) \dots s_N(t)[/math] w danej chwili [math]t[/math].

Pierwszą miarą użyteczną w tym przypadku będzie wspomniana już korelacja, opisująca podobieństwo dwóch mierzonych jednocześnie sygnałów. Istnienie opóźnień czasowych między sygnałami wykaże wspomniana również funkcja korelacji wzajemnej, mierząca podobieństwo dwóch sygnałów w funkcji przesunięcia w czasie jednego z nich. Z kolei funkcja koherencji opisuje podobieństwo dwóch sygnałów w funkcji częstości.

Trudniejszym zadaniem jest próba jednoczesnego uwzględnienia zależności między wszystkimi dostępnymi sygnałami. Stosuje się tu wiele metod, zarówno wywodzących się ze statystyki (jak analiza składowych głównych czy analiza czynnikowa) jak i opracowywanych specjalnie na potrzeby analizy sygnałów, jak wielowymiarowy model AR czy analiza składowych niezależnych. Dla przykładu opiszemy w skrócie niektóre z nich.

Analiza Składowych Głównych (PCA)

Analiza składowych głównych (Principal Component Analysis , PCA) znajduje bazę, w której macierz kowariancji [math]c_{ij}[/math] sygnału wielowymiarowego [math]\vec{s}[/math] przyjmuje postać diagonalną (baza Karhunena—Loève). Macierz transformacji [math]B[/math] obliczamy zwykle znaną z algeby metodą:

1. Wartości własne macierzy kowariancji znajdujemy z równania [math]|C-\lambda I|=0[/math]: [math]\begin{vmatrix} c_{11}-\lambda & c_{12} & \dots & c_{1N}\\ c_{21} & c_{22}-\lambda & \dots & c_{2N}\\ &&\ddots&\\ c_{N1} & c_{N2} & \dots &c_{NN}-\lambda \end{vmatrix}=0 [/math]
2. wektory własne [math]\vec{b}_i[/math], odpowiadające wartościon własnym [math]\lambda_i[/math], spełniają [math]C\vec{b_i}=\lambda_i \vec{b_i}[/math],
3. normalizujemy [math]\vec{b_i}[/math]. Wyznaczają one kierunki nowego układu współrzędnych, a złożona z nich macierz [math]B[/math] odpowiada obrotowi diagonalizującemu macierz kowariancji [math]C[/math].

Kierunki składowych PCA w dwóch wymiarach

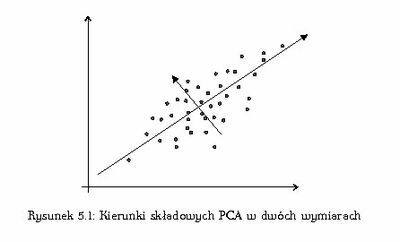
Celem jest zwykle redukcja wymiaru przez odrzucenie współrzędnych odpowiadających mniejszym wartościon [math]\lambda_i[/math] lub też poszukiwanie nowych współrzędnych per se (rys. %i 1).

Analiza składowych niezależnych (ICA)

Analiza składowych niezależnych (Independent Components Analysis , ICA) to jedno z określeń dla metod rozwiązywania problemu tzw. ślepej separacji źródeł (blind source separation, BSS). Przyjęty model zakłada, że mamy do czynienia z następującą sytuacją: dane którymi dysponujemy ([math]\vec{x}[/math] — np. zapisy z kilku mikrofonów) są liniową mieszaniną kilku statystycznie niezależnych sygnałów ([math]\vec{s}[/math] — np. głosy kilku mówiących jednocześnie osób, tzw. cocktail party problem):

[math] \vec{x} = A \vec{s} [/math]

[math]A[/math] zwiemy macierzą mieszającą, a rozwiązania szukamy w postaci macierzy separującej [math]B[/math], takiej, że wektor sygnałów

[math] \vec{y}=B\vec{x} [/math]

jest możliwie bliski (nieznanym) sygnałom [math]\vec{s}[/math]. Wymóg niezależności statystycznej elementów [math]\vec{y}[/math] wymaga uwzględnienia statystyk rzędów wyższych niż 2, czyli korelacji (używanych w PCA). Przetwarzanie wstępne polega często na wyzerowaniu statystyk do rzędu 2, czy odjęciu średniej i obrocie diagonalizującym macierz kowariancji (zwykle PCA). Uzyskanie w prosty sposób dekorelacji ułatwia działanie procedur realizujących dalsze wymagania niezależności. Realizowane są one zwykle z pomocą sztucznych sieci neuronowych o specjalnie dobieranych regułach uczenia.

Metodę w obecnej postaci wprowadzono do analizy sygnału w roku 1995 i większość aktualnych publikacji i algorytmów znaleźć można w Internecie.

Common Spatial Patterns (CSP)

Niech [math]\mathbf{X}_1[/math] wymiaru [math](n,t_1)[/math] i [math]\mathbf{X}_2[/math] wymiaru [math](n,t_2)[/math] -- dwa okna sygnału wielozmiennego, gdzie [math]n[/math] to liczba kanałów a [math]t_1[/math] i [math]t_2[/math] to odp. długości okien.

Algorytm CSP znajduje macierz [math]\mathbf{w}[/math] która maksymalizuje stosunek wariancji w oknach:

[math]\mathbf{w}={\arg \max}_\mathbf{w} \frac{ \left\| \mathbf{wX}_1 \right\| ^2 } { \left\| \mathbf{wX}_2 \right\| ^2 }[/math]

Wielozmienny model AR

Model AR opisuje wartość sygnału w chwili [math]t[/math] jako kombinację liniową jego wartości w chwilach poprzednich (oraz szumu). W przypadku wielowymiarowym możemy włączyć do tego opisu wartości wszystkich sygnałów [math]s_i[/math], czyli wektora [math]\vec{s}(t)[/math]. Wielozmienny model AR (MVAR, multivariate autoregressive ) można wówczas opisać wzorem:

[math] \vec{s}(t)=\sum_{i=1}^p A(i) \vec{s}(t-i) + \vec{\epsilon}(t) , [/math]

gdzie [math]\vec{\epsilon}(t)[/math] będzie wektorem szumów, zaś [math]A(i)[/math] będzie macierzą współczynników modelu. Przechodząc do przestrzeni częstości otrzymamy:

[math] \vec{s}(\omega)=A^{-1}(\omega)\vec{\epsilon}(\omega)=H(\omega)\vec{\epsilon}(\omega), [/math]

gdzie [math]H(\omega)[/math] jest macierzą przejścia. MVAR jest modelem typu "czarna skrzynka", gdzie na wejściu występują szumy, na wyjściu sygnały, a system jest opisany przez macierz przejścia. Zawiera on informacje o własnościach widmowych sygnałów i związkach między nimi.

Na podstawie macierzy [math]H(\omega)[/math] można obliczyć macierz gęstości widmowej zawierającą widma mocy dla pojedynczych kanałów jak również funkcje wzajemnej gęstości mocy pomiędzy kanałami. Stosując tego typu podejście, w którym wszystkie sygnały generowane przez pewien proces są rozpatrywane jednocześnie, można policzyć z macierzy spektralnej nie tylko koherencje zwykłe pomiędzy dwoma kanałami, ale również koherencje wielorakie opisujące związek danego kanału z pozostałymi i koherencje cząstkowe opisujące bezpośrednie związki między dwoma kanałami po usunięciu wpływu pozostałych kanałów. W przypadku gdy pewien kanał 1 będzie wpływał na kanały 2 i 3, obliczając koherencję zwykłą znajdziemy związek między 2 oraz 3, chociaż nie są one ze sobą bezpośrednio powiązane, natomiast koherencja cząstkowa nie wykaże związku między nimi.

Macierz [math]H(\omega)[/math] jest niesymetryczna, a jej wyrazy pozadiagonalne mają sens przyczynowości Grangera, co oznacza, że uwzględnienie wcześniejszej informacji zawartej w jednym z sygnałów zmniejsza błąd predykcji drugiego sygnału. Opierając się na tej własności zdefiniowano Kierunkową Funkcję Przejścia (DTF, directed transfer function) jako znormalizowany element pozadiagonalny [math]H(\omega)[/math]. DTF opisuje kierunek propagacji i skład widmowy rozchodzących się sygnałów.

Otrzymamy w ten sposób całościowy opis zmian wszystkich sygnałów jednocześnie. Co ciekawe, obliczona na tej podstawie funkcja charakteryzująca zależności między sygnałami [math]s_i[/math] (funkcja przejścia) nie jest symetryczna, w przeciwieństwie do np. korelacji. Dzięki temu może służyć wnioskowaniu nie tylko o sile zależności między poszczególnymi sygnałami składowymi, ale też o kierunku przepływu informacji między nimi. W przybliżeniu odpowiada to informacji, w którym z sygnałów struktury odpowiadające danej częstości pojawiają się wcześniej.