Pracownia EEG/ERDS 2
Pracownia EEG / Czas-częstość
Spis treści
- 1 Estymacja i analiza względnych zmian gęstości energii sygnału EEG w przestrzeni czas-częstość
Estymacja i analiza względnych zmian gęstości energii sygnału EEG w przestrzeni czas-częstość
import numpy as np
import pylab as py
import scipy.signal as ss
def czas(T = 1.0, Fs = 128.0):
dt = 1.0/Fs
t = np.arange(0,T,dt)
return t
def gauss(t0 = 0.3, sigma = 0.02, T = 1.0, Fs = 128.0):
t = czas(T,Fs)
s = np.exp(-((t-t0)/(sigma))**2/2)
return s
def g2(t0 = 0.3, sigma = 0.02, T = 1.0, Fs = 128.0):
t = czas(T,Fs)
s = (-(t-t0)/(sigma))*np.exp(-((t-t0)/(sigma))**2/2)
return s
def g3(t0 = 0.3, sigma = 0.02, T = 1.0, Fs = 128.0):
t = czas(T,Fs)
s = np.exp(-((t-t0)/(sigma))**2/2)
s[t<t0] = 0
return s
def gabor(t0 = 0.5, sigma = 0.1, T = 1.0, f=10, phi = 0, Fs = 128.0):
t = czas(T,Fs)
s = np.exp(-((t-t0)/(sigma))**2/2) * np.cos(2*np.pi*f*(t-t0) + phi)
return s
def sin(f = 10.0, T = 1.0, Fs = 128.0, phi =0 ):
'''sin o zadanej cz?sto?ci (w Hz), d?ugo?ci, fazie i cz?sto?ci próbkowania
Domy?lnie wytwarzany jest sygna? reprezentuj?cy
1 sekund? sinusa o cz?sto?ci 1Hz i zerowej fazie próbkowanego 128 Hz
'''
t = czas(T,Fs)
s = np.sin(2*np.pi*f*t + phi)
return s
def chirp(f0,fk,T,Fs):
t = czas(T,Fs)
f = f0 + (fk-f0)/2.0/(T)*t
s = np.cos(2*np.pi*t*f)
return s
def cwt(x, MinF,MaxF,Fs,w=7.0,df=1.0,plot = True):
'''w - parametr falki Morleta,
wiaze sie z jej czestoscia centralna i skala w nastepujacy sposob:
f = 2*s*w / T
gdzie: s-skala, T-dlugosc sygnalu w sek.'''
T= len(x)/Fs
M = len(x)
t = np.arange(0,T,1./Fs)
freqs = np.arange(MinF,MaxF,df)
P = np.zeros((len(freqs),M))
X = ss.fft(x)
for i,f in enumerate(freqs):
s = T*f/(2*w)
psi = ss.fft(ss.morlet(M, w=w, s=s, complete=True))
psi /= np.sqrt(np.sum(psi*psi.conj()))
tmp = np.fft.fftshift(ss.ifft(X*psi))
P[i,:] = (tmp*tmp.conj()).real
if plot:
py.imshow(P,aspect='auto',origin='lower',extent=(0,T,MinF, MaxF))
py.show()
return P,f,t
def wvd(x, Fs, plot=True):
samples = len(x)
N = samples / 2
z = np.zeros(samples)
xh = ss.hilbert(x)
x_period_h = np.concatenate((z,xh,z));
t = range(0, samples, 1) # czas w samplach
tfr = np.zeros((samples , samples), dtype=complex)
for ti in t:
for tau in range(-samples/2,samples/2):
tfr[samples/2 + tau, ti] = x_period_h[samples+ti + tau] * x_period_h[samples+ti - tau].conj()
tfr = np.fft.fftshift(tfr,axes = 0)
Tfr = np.fft.fft(tfr, samples, axis=0)/samples
ts = np.array(t, dtype=float) / (float(Fs))
f = np.linspace(0, Fs / 2, N)
if plot:
py.imshow( Tfr.real, interpolation='nearest', extent=[0, ts[-1], 0, f[-1]], origin='lower', aspect='auto')
py.show()
return Tfr, ts, f
if __name__ == '__main__':
t = czas()
Fs = 512.0
T = 1.0
#py.plot(t,sin(),t,gauss(),t,g2(),t,g3(),t,gabor())
ch = chirp(5,Fs/2-5,T,Fs)
py.plot(ch)
py.show()
#cwt(gabor(),0.1,64,128)
#cwt(ch,0.1,Fs/2,Fs)
#ch = gabor(t0=0,f=Fs/2)
wvd(ch,Fs)
Zasada nieoznaczoności dla przestrzeni czas-częstość
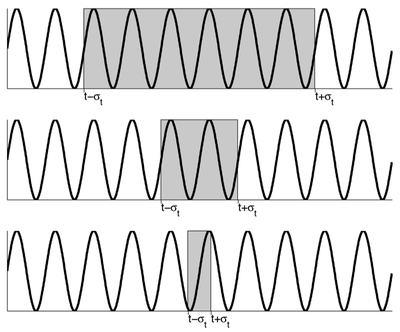
Poniższy rysunek obrazuje koncepcję zasady nieoznaczoności w przypadku analizy czas-częstość: im dokładniej znamy lokalizację interesującego nas fragmentu sygnału (struktury) w czasie tym mniej dokładnie możemy poznać jego częstość.
Zasadę tą można wyrazić formalnie w następujący sposób. Potraktujmy moc sygnału [math]x(t)[/math] (o skończonej energii) jak rozkład zmiennej losowej. Aby rozkład był unormowany trzeba podzielić go przez energię sygnału: [math]E_x = \int_{-\infty}^{\infty} |x(t)|^2 dt \lt \infty[/math]. Zatem rozkład ten jest postaci: [math]p(t) = \frac{1}{E_x}|x(t)|^2 [/math].
Jako lokalizację występowania sygnału w czasie przyjmujemy średnie położenie jego energii:
- [math]t_0 = \frac{1}{E_x} \int_{-\infty}^{\infty}t |x(t)|^2 dt[/math]
zaś jako miarę skupienia energii wokół tego położenia przyjmujemy wariancję:
- [math]\sigma_t^2 = \frac{1}{E_x}\int_{-\infty}^{\infty} (t - t_0)^2 |x(t)|^2 dt [/math]
Analogicznie w dziedzinie częstości:
- [math]f_0 = \frac{1}{E_x} \int_{-\infty}^{\infty}f |X(f)|^2 df[/math]
- [math]\sigma_f^2 = \frac{1}{E_x}\int_{-\infty}^{\infty} (f - f_0)^2 |X(f)|^2 df [/math]
Można pokazać (np. Pinsky, 2002), że iloczyn wariancji energii w czasie i w częstości jest ograniczony od dołu:
- [math]\sigma_t^2 \sigma_f^2 \ge \frac{1}{16 \pi^2}[/math]
Estymatory gęstości widmowej dla przestrzeni czas-częstość
Energię sygnału w jednej z dziedzin, czasu bądź częstości, możemy policzyć tak:
- [math] E_x=\int_{-\infty}^{\infty}{|x(t)|^2 dt} = \int_{-\infty}^{\infty}{|X(f)|^2 df}[/math]
i interpretujemy [math]|x(t)|^2[/math] albo [math]|X(f)|^2[/math] jako gęstości energii. Stąd pomysł, żeby rozszerzyć tą koncepcję na obie dziedziny jednocześnie i wprowadzić pojęcie gęstości energii w dziedzinie czas-częstość [math]\rho_x(t,f)[/math]:
- [math] E_x=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}{\rho_x(t,f) dt df}[/math]
muszą też być spełnione własności brzegowe:
- [math] \int_{-\infty}^{\infty}{\rho_x(t,f) dt}=|X(f)|^2[/math]
- [math] \int_{-\infty}^{\infty}{\rho_x(t,f) df} = |x(t)|^2[/math]
Dystrybucja energii
Podobnie jak widmo mocy, gęstość energii fizycznego sygnału nie może być obliczona, może być jedynie estymowana. W celu estymacji gęstości energii można posłużyć się dwuwymiarowymi dystrybucjami energii. Jedną z podstawowych dystrybucji jest dystrybucja Wigner-Ville'a (WVD):
- [math] W_x(t,f)=\int_{-\infty}^{\infty}x(t+\tau/2)x^*(t-\tau/2)e^{-i 2 \pi f \tau} d\tau[/math]
lub
- [math] W_x(t,f) = \int_{-\infty}^{\infty} X(f+\xi/2)X^*(f-\xi/2) e^{i 2 \pi \xi t} d\xi[/math]
Implementacja
Przykładowa implementacja WVD dla sygnału rzeczywistego:
import numpy as np
import pylab as py
import scipy.signal as ss
def wvd(x, Fs, plot=True):
samples = len(x)
N = samples / 2
z = np.zeros(samples)
xh = ss.hilbert(x)
x_period_h = np.concatenate((z,xh,z));
t = range(0, samples, 1) # czas w samplach
tfr = np.zeros((samples , samples), dtype=complex)
for ti in t:
for tau in range(-samples/2,samples/2):
tfr[samples/2 + tau, ti] = x_period_h[samples+ti + tau] * x_period_h[samples+ti - tau].conj()
tfr = np.fft.fftshift(tfr,axes = 0)
Tfr = np.fft.fft(tfr, samples, axis=0)/samples
ts = np.array(t, dtype=float) / (float(Fs))
f = np.linspace(0, Fs / 2, N)
if plot:
py.imshow( Tfr.real, interpolation='nearest', extent=[0, ts[-1], 0, f[-1]], origin='lower', aspect='auto')
py.show()
return Tfr, ts, f
Własności
Własności WVD:
- zachowanie energii
- własności brzegowe
- zachowywanie przesunięcia w czasie i w częstości
- [math] y(t) = x(t-t_0) \Rightarrow W_y(t,f) = W_x(t-t_0,f)[/math]
- [math] y(t) = x(t)e^{i 2 \pi f_0 t} \Rightarrow W_y(t,f) = W_x(t,f-f_0)[/math]
- zachowywanie skalowania
- [math] y(t)=\sqrt{k}x(kt) \Rightarrow W_y(t,f) = W_x(kt, f/k)[/math]
Wyrazy mieszane
WVD jest reprezentacją kwadratową więc:
- [math] y(t) = x_1(t)+x_2(t) \Rightarrow W_y(t, f) = W_{x_1}(t, f)+W_{x_2}(t, f)+W_{x_1,x_2}(t, f)+W_{x_2,x_1}(t, f)[/math]
gdzie
- [math] W_{x_1,x_2}(t, f) = \int_{-\infty}^{\infty} x_1(t+\tau/2)x_2^*(t-\tau/2)e^{-i 2 \pi f \tau} d\tau[/math]
Rozdzielczość
- idealnie dla chirpów liniowych (sygnał o liniowo zmieniającej się częstości chwilowej):
import tf as tf
import pylab as py
Fs = 512.0
T = 1.0
t = tf.czas(T,Fs)
ch = tf.chirp(5,Fs/2-5,T,Fs)
Tfr,ts,f = tf.wvd(ch,Fs,False)
py.subplot(2,1,1)
py.plot(t,ch)
py.subplot(2,1,2)
py.imshow(Tfr.real,interpolation= 'nearest',extent=[0,ts[-1],0,f[-1]],origin='lower',aspect='auto')
py.show()
- struktura wyrazów mieszanych: zaobserwuj, że niezależnie od tego jak bardzo odseparowane są struktury w przestrzeni czas-częstość pomiędzy nimi powstają wyrazy mieszane. Zauważ, że wyrazy mieszane mają wysoką częstość przestrzennej zmienności.
import tf as tf
import pylab as py
Fs = 512.0
T = 1.0
t = tf.czas(T,Fs)
s1 = tf.gabor(t0=0.3, sigma = 0.05, T = 1.0, f=100, phi = 0,Fs=Fs)
s2 = tf.gabor(t0=0.7, sigma = 0.05, T = 1.0, f=200, phi = 0,Fs=Fs)
s = s1 + s2
Tfr,ts,f = tf.wvd(s,Fs,False)
py.subplot(2,1,1)
py.plot(t,s)
py.subplot(2,1,2)
py.imshow(Tfr.real,interpolation= 'nearest',extent=[0,ts[-1],0,f[-1]],origin='lower',aspect='auto')
py.show()
Klasa Cohena
WVD jest najprostszym elementem klasy Cohena. Ogólnie klasę tę można zapisać jako:
- [math] C_x(t,f,\Pi) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \Pi(s-t, \xi - f) W_x(s,\xi) ds d\xi[/math]
gdzie
- [math] \Pi(t,f) = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty} f(\xi, \tau) e^{-i 2 \pi (f\tau + \xi t)} dt df[/math]
Najczęściej [math] \Pi[/math] wybiera się jako pewną funkcję gładzącą — w zależności od tego wyboru będziemy mieli w różnym stopniu osłabiane wyrazy mieszane.
MP — dopasowanie kroczące
Definicja
Algorytm dopasowania kroczącego (ang. matching pursuit, MP) jest algorytmem iteracyjnie rozkładającym sygnał [math]s(t)[/math] na funkcje bazowe (tzw. atomy czas-częstość) [math]g_{\gamma_n}[/math] pochodzące ze zbioru [math]D[/math] (zwanego słownikiem):
- [math] \left \{ \begin{array}{l} R^0s = s\\ R^ns = \langle R^ns,g_{\gamma_n} \rangle g_{\gamma_n}+R^{n+1}s\\ g_{\gamma_n} = \arg \max_{g_{\gamma_i} \in D } |\langle R^ns, g_{\gamma_i}\rangle| \end{array} \right . [/math]
gdzie: [math]\arg \max_{g_{\gamma_i} \in D }[/math] oznacza tego [math] g_{\gamma_i}[/math], który daje największy iloczyn skalarny z aktualnym residuum: [math]|\langle R^ns, g_{\gamma_i}\rangle|[/math].
Słowniki mogą być dowolne, ale najczęściej składamy je z funkcji Diraca, sinus i Gabora:
- [math] g_\gamma (t) = K(\gamma)e^{ -\pi\left( \frac{t-u}{\sigma} \right)^2} \sin\left(2 \pi f (t-u)+\phi\right) [/math]
normalizacja [math] K(\gamma)[/math] jest taka, że [math] ||g_{\gamma}||=1[/math], [math]\gamma=\{ u, f, \sigma, \phi \}[/math] to parametry funkcji w słowniku ([math]u[/math] — translacja w czasie, [math] f[/math] — częstość, [math] \sigma[/math] — szerokość w czasie, [math] \phi[/math] — faza).
Dystrybucja energii
Reprezentację czas-częstość uzyskujemy z dekompozycji MP sumując dystrybucje WVD pojedynczych atomów:
- [math] W_{ g_{\gamma_n}}(t, f)=\int g_{\gamma_n} \bigl (t + \frac{\tau}{2} \bigr)\; g_{\gamma_n}^*\left(t- \frac{\tau}{2} \right) e^{- i 2 \pi f \tau } d \tau [/math]
- [math] E^{MP} = \sum_{n=0}^M |\langle R^n s, \;g_{\gamma_n} \rangle|^2 \; W_{g_{\gamma_n}} (t, f) [/math]
W wyrażeniu tym nie ma wyrazów mieszanych :-)
Krótkoczasowa transformacja Fouriera i spektrogram
Definicja krótkoczasowej transformacji Fouriera
Krótkoczasowa transformacja Fouriera (ang. short-time Fourier transform, STFT) może być rozumiana jako seria transformacji Fouriera wykonanych na sygnale podzielonym na okienka, przy czym położenie okienka w czasie jest w ramach takiej serii przesuwane monotonicznie. W wersji ciągłej możemy to zapisać tak:
- [math]F_x(t,f; h)= \int_{-\infty}^{\infty}{x(u) h^*(u-t)e^{- i 2 \pi u f} du} [/math]
Własności
Jeśli okienko ma skończoną energię to STFT jest transformacją odwracalną i można odzyskać z niej sygnał w reprezentacji czasowej:
- [math] x(t) = \frac{1}{E_h}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}F_x(u,f;h)h(t-u)e^{i 2\pi t f}\,du\,df [/math]
gdzie [math]E_h=\int_{-\infty}^{\infty}|h(t)|^2\,dt [/math] Tak więc sygnał może być rozłożony na liniową kombinację elementarnych falek-„atomów” postaci:
- [math]h_{t,f}(u)=h(u-t)e^{i 2 \pi f u}[/math]
Każdy atom uzyskiwany jest przez translację pojedynczego okna [math]h[/math] w czasie i jego modulację częstością [math]f[/math].
Ciekawostka: zbiór wszystkich możliwych transformacji tego typu tworzy grupę Weyl-Heisenberga.
Spektrogram
Definicja
Spektrogram: kwadrat modułu STFT jest estymatą gęstości energii w przestrzeni czas-częstość:
- [math]S_x(t, f) =\left|\int_{-\infty}^{\infty}{x(u) h^*(u - t) e^{-i 2\pi f u} du}\right|^2[/math]
Implementacja
Spektrogram zaiplementowany jest w module matplotlib.pyplot jako funkcja specgram (dokumentacja).
Własności
Przesunięcia
Spektrogram zachowuje przesunięcie:
w czasie
- [math]y(t) = x(t - t_0)\Rightarrow S_y(t, f; h) = S_x(t - t_0, f; h)[/math]
import matplotlib.pyplot as py
from tf import czas, gabor
import numpy as np
import scipy.signal as ss
# parametry
t0 = 1.0
sigma = 0.1
T = 4.0
f = 10
phi = 0
Fs = 128.0
NFFT = int(Fs)
sig1 = gabor(t0, sigma, T, f, phi, Fs) # sygnał
sig2 = gabor(t0 + 2, sigma, T, f, phi, Fs) # sygnał przesunięty w czasie
py.subplot(221)
h = ss.hamming(NFFT)
sig1_padded = (np.concatenate((np.zeros(NFFT/2),sig1,np.zeros(NFFT/2))))
P,f,t,im1 = py.specgram(sig1_padded,NFFT = len(h),Fs = Fs,window = h, noverlap = NFFT-1, sides = 'onesided')
py.imshow(P,aspect='auto',origin='lower',extent=(t[0]-(NFFT/2)/Fs,t[-1]-(NFFT/2)/Fs,f[0],f[-1]),interpolation='nearest')
py.subplot(222)
sig2_padded = (np.concatenate((np.zeros(NFFT/2),sig2,np.zeros(NFFT/2))))
P,f,t,im2 = py.specgram(sig2_padded,NFFT = len(h),Fs = Fs,window = h, noverlap = NFFT-1, sides = 'onesided')
py.imshow(P,aspect='auto',origin='lower',extent=(t[0]-(NFFT/2)/Fs,t[-1]-(NFFT/2)/Fs,f[0],f[-1]),interpolation='nearest')
py.subplot(223)
time = czas(T, Fs)
py.plot(time,sig1)
py.subplot(224)
py.plot(time ,sig2)
py.show()
i w częstości:
- [math]y(t) = x(t) e ^{i 2 \pi f_0 t}\Rightarrow S_y(t, f; h) = S_x(t, f - f_0; h)[/math]
import matplotlib.pyplot as py
from tf import czas, gabor
import numpy as np
import scipy.signal as ss
# parametry
t0 = 1.0
sigma = 0.1
T = 4.0
f = 10
phi = 0
Fs = 128.0
NFFT = int(Fs)
time = czas(T, Fs)
sig1 = gabor(t0, sigma, T, f, phi, Fs) # sygnał
sig2 = gabor(t0, sigma, T, f+20, phi, Fs)# sygnał przesunięty w częstości
py.subplot(221)
h = ss.hamming(NFFT)
sig1_padded = (np.concatenate((np.zeros(NFFT/2),sig1,np.zeros(NFFT/2))))
P,f,t,im1 = py.specgram(sig1_padded,NFFT = len(h),Fs = Fs,window = h, noverlap = NFFT-1, sides = 'onesided')
py.imshow(P,aspect='auto',origin='lower',extent=(t[0]-(NFFT/2)/Fs,t[-1]-(NFFT/2)/Fs,f[0],f[-1]),interpolation='nearest')
py.subplot(222)
sig2_padded = (np.concatenate((np.zeros(NFFT/2),sig2,np.zeros(NFFT/2))))
P,f,t,im2 = py.specgram(sig2_padded,NFFT = len(h),Fs = Fs,window = h, noverlap = NFFT-1, sides = 'onesided')
py.imshow(P,aspect='auto',origin='lower',extent=(t[0]-(NFFT/2)/Fs,t[-1]-(NFFT/2)/Fs,f[0],f[-1]),interpolation='nearest')
py.subplot(223)
py.plot(time,sig1)
py.subplot(224)
py.plot(time ,sig2)
py.show()
Wyrazy mieszane
Spektrogram jest reprezentacją kwadratową. Spektrogram sumy sygnałów nie jest sumą spektrogramów sygnałów składowych, jest tam jeszcze coś:
- [math]y(t) = x_1(t)+x_2(t) \Rightarrow S_y(t, f) = S_{x_1}(t, f)+S_{x_2}(t, f)+S_{x_1,x_2}(t, f)+S_{x_2,x_1}(t, f)[/math]
gdzie
- [math]S_{x_1,x_2}(t, f) = F_{x_1}(t, f)F^*_{x_2}(t, f)[/math]
Jak mogą wyglądać wyrazy mieszane ilustruje poniższy kod. Kolejne subploty pokazują spektrogramy uzyskane dla sygnału będącego sumą dwóch funkcji Gabora o częstościach różniących się o 2 Hz i położeniach różniących się o kolejne wielokrotności 0,1 s.
import matplotlib.pyplot as py
from tf import czas, gabor
import numpy as np
import scipy.signal as ss
# parametry
t0 = 1.0
sigma = 0.05
T = 2.0
f0 = 20
phi = 0
Fs = 128.0
NFFT = int(Fs)
time = czas(T, Fs)
h = ss.hamming(NFFT)
for i in range(9):
py.subplot(3,3,i+1)
sig1 = gabor(t0, sigma, T, f0, phi, Fs) # sygnal
sig2 = gabor(t0+i*0.1, sigma, T, f0+2, phi, Fs)# sygnał przesunięty w częstości o 2 Hz i w czasie o i*0.1 s
sig1_padded = (np.concatenate((np.zeros(NFFT/2),sig1,np.zeros(NFFT/2))))
sig2_padded = (np.concatenate((np.zeros(NFFT/2),sig2,np.zeros(NFFT/2))))
P,f,t,im1 = py.specgram(sig1_padded+sig2_padded,NFFT = len(h),Fs = Fs,window = h, noverlap = NFFT-1, sides = 'onesided')
py.imshow(P,aspect='auto',origin='lower',extent=(t[0]-(NFFT/2)/Fs,t[-1]-(NFFT/2)/Fs,f[0],f[-1]),interpolation='nearest')
py.show()
Wyrazy mieszane występują także w przypadku pojedynczej struktury dla sygnału rzeczywistego. „Mieszające się” obiekty to energia zlokalizowana w dodatniej i ujemnej części widma częstości. Efekt jest stosunkowo słaby i uwidacznia się dopiero na mapach czas-częstość logarytmu gęstości energii. Problem ten można obejść stosując transformację Hilberta, gdyż po tej transformacji cała energia skupiona jest w dodatniej części widma. Własność tę ilustruje poniższy program:
from matplotlib.pyplot import specgram, plot, subplot, show, imshow
from tf import czas, gabor
from numpy import pi, log
from scipy.signal import hamming, hilbert
# parametry
t0 = 0.5
sigma = 0.1
T = 1.0
f = 30
phi = 0
Fs = 256.0
s = gabor(t0, sigma, T, f, phi, Fs)
t = czas(T, Fs)
subplot(411)
plot(t,s)
subplot(412)
h = hamming(32)
NFFT =len(h)
P,f,t,im1 = specgram(s,NFFT = len(h),Fs = Fs,window = h, noverlap = 31,sides = 'twosided')
imshow(P,aspect='auto',origin='lower',extent=(t[0]-(NFFT/2)/Fs,t[-1]-(NFFT/2)/Fs,f[0],f[-1]),interpolation='nearest')
subplot(413)
imshow(log(P),aspect='auto',origin='lower',extent=(t[0]-(NFFT/2)/Fs,t[-1]-(NFFT/2)/Fs,f[0],f[-1]),interpolation='nearest')
subplot(414)
s_ana = hilbert(s) # sygnał analityczny
P,f,t,im2 = specgram(s_ana,NFFT = len(h),Fs = Fs,window = h, noverlap = 31, sides = 'twosided')
imshow(log(P),aspect='auto',origin='lower',extent=(t[0]-(NFFT/2)/Fs,t[-1]-(NFFT/2)/Fs,f[0],f[-1]),interpolation='nearest')
show()
Ćwiczenie:
- Proszę zbadać rozdzielczość czasową spektrogramu posługując się funkcją delta oraz rozdzielczość częstotliwościową posługując się funkcją sinus (Trzeba „przeskanować” czas funkcją delta, a częstości sinusem). Proszę wykonać to dla kilku długości okienek h.
- Proszę zbadać rozdzielczość spektrogramu przy pomocy dwóch funkcji Gabora, dla różnych ich odległości w czasie i w częstości. Zaobserwować strukturę wyrazów mieszanych.
Ciągła transformata falkowa i skalogram
Ciągłą transformata falkowa
Definicja
Ciągła transformacja falkowa (ang. Continuous Wavelet Transform, CWT) dana jest wzorem:
- [math] P_x(t,a;\Psi)= \int_{-\infty}^{\infty}{x(s)\Psi^*_{t,a}(s) ds}[/math]
gdzie
- [math] \Psi_{t,a}(s) = \frac{1}{\sqrt{|a|}} \Psi\left(\frac{s-t}{a}\right)[/math]
a jest skalą. Od falki [math]\Psi[/math] wymagamy żeby miała średnią 0.
Transformację tę można interpretować jako rzutowanie sygnału na kolejne wersje falki [math]\Psi[/math] przesunięte o t i przeskalowane o a.
Inne spojrzenie na transformację falkową uwidacznia się gdy połączymy dwa powyższe wzory:
- [math]P_x(t,a;\Psi)= \frac{1}{\sqrt{|a|}}\int_{-\infty}^{\infty}{x(s) \Psi^*\left(\frac{s-t}{a}\right) ds} [/math]
Tu widać, że dla ustalonej skali a transformacja falkowa jest splotem sygnału z falką o skali a. Ten sposób myślenia o transformacji falkowej umożliwia zastosowanie szybkiego algorytmu obliczeniowego bazującego na tym, że splot w dziedzinie czasu odpowiada mnożeniu w dziedzinie częstości.
Skalogram
Podobnie jak dla STFT i spektrogramu, możemy dla CWT wprowadzić pojęcie skalogramu, będącego estymatą gęstości energii w przestrzeni czas-skala.
- [math]S_x(t,a;\Psi)=\left| P_x(t,a;\Psi)\right|^2[/math]
Dla falek, które są dobrze skupione wokół częstości [math]f_0[/math] dla skali [math]a_0=1[/math] można wprowadzić utożsamienie [math]f=\frac{f_0}{a}[/math]. Utożsamienie to pozwala przekształcić reprezentację czas-skala w reprezentację czas-częstość:
- [math]S_x(t,f;\Psi)=\left| P_x(t,f_0/f;\Psi)\right|^2[/math]
Implementacja
Przykładowa implementacja obliczania skalogramu dla falek Morleta przedstawiona jest poniżej. Korzysta ona z własności splotu.
def cwt(x, MinF,MaxF,Fs,w=7.0,df =1.0,plot = True):
'''w - parametr falki Morleta,
wiąże się z jej częstościa centralną i skalą w następujacy sposób:
f = 2*a*w / T
gdzie: a-skala, T-długość sygnału w sek.'''
T= len(x)/Fs
M = len(x)
t = np.arange(0,T,1./Fs)
freqs = np.arange(MinF,MaxF,df)
P = np.zeros((len(freqs),M))
X = np.fft.fft(x) # transformacja sygnału do dziedziny czestosci
for i,f in enumerate(freqs): # petla po kolejnych czestosciach
a = T*f/(2*w) # obliczenie skali dla danej czestosci
psi = np.fft.fft(ss.morlet(M, w=w, s=a, complete=True)) # transformacja falki Morleta do dziedziny czestosci. W bardziej wydajnym kodzie moznaby zastosowac analityczna postac tej falki w dziedzinie czestosci.
psi /= np.sqrt(np.sum(psi*psi.conj())) # normalizacja energii falki
CWT = np.fft.fftshift(ss.ifft(X*psi))
P[i,:] = (CWT*CWT.conj()).real
if plot:
py.imshow(P,aspect='auto',origin='lower',extent=(0,T,MinF, MaxF))
py.show()
return P,f,t
Matching pursuit
Dopasowanie kroczące (ang. matching pursuit, MP) jest procedurą polegającą na rozłożeniu sygnału na funkcje składowe pochodzące z określonego zbioru funkcji (słownika). Słowniki wykorzystywane w metodach czas-częstość często składają się z funkcji Gabora tj. funkcji sinus modulowanej funkcją Gaussa. MP jest algorytmem iteracyjnym. W pierwszym kroku wybierana jest funkcja dająca największy iloczyn skalarny z sygnałem. W każdym następnym kroku funkcja jest analogicznie dopasowywana do residuum sygnału, pozostałego po odjęciu wyniku poprzedniej iteracji.
Ćwiczenia
Zadanie 1
- Zapoznać się z opisem metod czas-częstość, wykonując polecenia opisane przy każdej z metod.
- Zbadać własności metod czas-częstość, m.in.:
- Proszę przyjrzeć się definicjom transformaty falkowej i STFT i opowiedzieć o analogiach i różnicach.
- Proszę zbadać własności przesunięć w czasie i w częstości dla skalogramu w sposób analogiczny jak było to pokazane dla spektrogramu.
- Proszę zbadać strukturę wyrazów mieszanych w sposób analogiczny jak było to pokazane dla spektrogramu.
Zadanie 2
Zbadaj działanie algorytmu MP na samodzielnie wytworzonych sygnałach symulowanych:
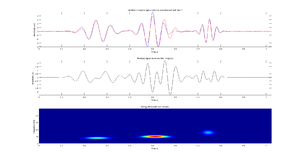
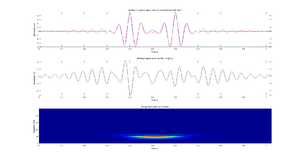
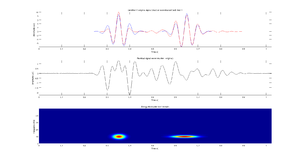
- Trzech funkcjach Gabora o różnych częstościach, amplitudach i położeniach w czasie i o podobnej rozciągłości w czasie tak, aby zasadniczo nie nachodziły na siebie (patrz rysunek). Wykonaj dopasowanie dla trzech atomów, narysuj sygnał oryginalny i nałożony na niego sygnał zrekonstruowany z wyliczonych atomów, różnicę tych sygnałów (residuum) oraz mapę czas-częstość.
- Dwóch jednakowych funkcji Gabora położonych w pewnej odległości od siebie w czasie. Zbadaj jakość dopasowania dokonując rekonstrukcji dwoma i trzema atomami na rysunkach podobnych jak w poprzedniej części zadania. Sprawdź co się dzieje przy zwiększaniu odległości w czasie pomiędzy tymi funkcjami Gabora.
Zadanie 3
Sporządź mapy czas-częstość
- kilku sygnałów zawierających artefakty;
- danych zawierających czynność alfa;
- sygnałów zawierających wzrokowe sygnały wywołane;
- sygnałów SSVEP.
Porównaj mapy uzyskane różnymi metodami: dekompozycją Wignera-Ville'a, spektrogramem, transformacją falkową i metodą MP. Wyróżnij struktury charakterystyczne dla poszczególnych rodzajów sygnałów.
Zadanie 4
Pobrać plik z danymi: https://www.fuw.edu.pl/~suffa/LabEEG/Characterize_ch4_F50_G4.mat
Opis danych: dane zawierają zapisy z lokalnych potencjałów polowych (LFP) z kory czuciowej małpy podczas podawania bodźca wibracyjnego do palca. Macierz zawiera 50 powtórzeń po 3 sekundy. Częstość próbkowania wynosi 5000 Hz. Bodziec podawany był pomiędzy 1 a 2 sekundą.
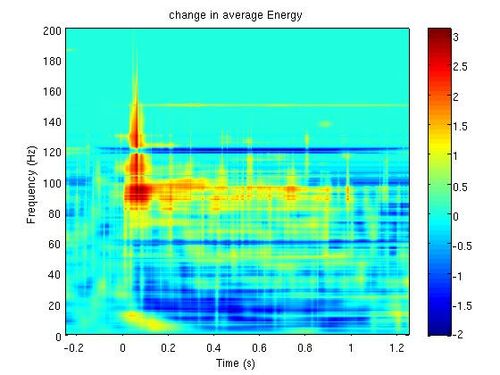
Zadania do wykonania:
- Otrzymać mapy czas-częstość dla pojedynczych realizacji a następnie uśrednić je po realizacjach.
- Na średniej mapie poszukać występowania odpowiedzi w częstościach high-gamma (100-200 Hz).
- W przypadku braku widocznej odpowiedzi, rozważyć następujące operacje:
- usunąć częstości sieci (60 Hz i wyższe harmoniczne);
- zastosować logarytmiczną skalę energii;
- policzyć zmiany gęstości energii względem jej wartości w okresie referencyjnym.
Mapa czas-częstość średniej gęstości energii otrzymaną metodą Matching Pursuit jest przedstawiona na rys. 1.
Zadanie 5
Wykonać analizę metodą MP dla danych z zadania 3.
Literatura
S. Mallat and Z. Zhang (1993) Matching pursuit with time-frequency dictionaries. IEEE Transactions on Signal Processing, 41:3397-3415.
Pinsky, Mark (2002), Introduction to Fourier Analysis and Wavelets, Brooks/Cole, ISBN 0-534-37660-6