Pracownia EEG 2/AR 1
Pracownia EEG 2 / Widmowa analiza parametryczna
Spis treści
Model autoregresyjny stochastycznego szeregu czasowego
Wstęp
Do tej pory, aby zbadać własności widmowe sygnałów, używaliśmy transformacji Fouriera. Sygnał X(t) z dziedziny czasu transformowaliśmy do dziedziny częstości X(f):
Następnie z transformaty estymowaliśmy funkcję gęstości widmowej mocy danego sygnału zgodnie ze wzorem:
Możliwe jest jednak trochę inne podejście: załóżmy, że nasz sygnał jest realizacją procesu stochastycznego opisanego pewną, znaną nam zależnością. Typowym założeniem w dziedzinie analizy sygnałów EEG jest opisanie ich jako procesów autoregresyjnych (AR):
Ze względu na charakter widma takiego procesu dobrze nadaje się on do opisu sygnałów składających się z kilku rytmów o częstościach zawierających się w pewnych zakresach oraz tła o charakterze szumu. EEG i wiele innych sygnałów biologicznych ma właśnie taką strukturę.
Co to znaczy opisać sygnał modelem AR? Musimy dopasować tak współczynniki A ze wzoru (Equation 3), czyli tzw. współczynniki modelu, aby realizowany za jego pomocą proces AR miał funkcję autokowariancji jak najbliższą do badanego sygnału. Jeśli się nam to uda, to wszystkie wnioski dotyczące badanego sygnału możemy wyciągać na podstawie analizy parametrów modelu, a nie wartości sygnału.
Parametryczna analiza widmowa
Równanie opisujące proces AR transformujemy do przestrzeni częstości za pomocą transformacji Z — jest to uogólnienie transformacji Fouriera stosowane dla dyskretnych ciągów wartości. Skorzystamy tu z faktu, że transformacja Z ma (podobnie do transformacji Fouriera) własność transformowania splotu sygnałów w iloczyn ich transformat. Zauważmy, że jeśli przepiszemy równanie (Equation 3) tak, aby włączyć X(t) do sumowania (możemy to zrobić przyjmując A(0) = 1 oraz zmieniając znak pozostałych współczynników), to po lewej stronie równania otrzymujemy splot ciągu współczynników A z ciągiem wartości X. Tak więc po przetransformowaniu tego równania otrzymujemy iloczyn odpowiednich transformat:
Z dziedziny zmiennej z możemy przejść do dziedziny częstości podstawiając z = e2πifΔt (f — częstość, Δt — odstęp czasu między kolejnymi próbkami sygnału):
Funkcję H(f) nazywamy macierzą przejścia modelu.
Gęstość widmową mocy uzyskamy ze znanej już zależności (Equation 2):
Opis własności sygnałów w języku modeli stochastycznych ma kilka zalet. Jedną z nich jest możliwość zastosowania w przypadku krótkich odcinków sygnału. Ale dla nas najważniejsza będzie łatwość modelowania sygnałów wielokanałowych przez jeden wielokanałowy model AR.
Wybór rzędu modelu
Przyglądając się równaniu (Equation 3) widzimy, że musimy również wiedzieć ile wcześniejszych próbek sygnału należy uwzględnić w naszych obliczeniach, czyli ustalić liczbę p. Liczbę tę nazywamy rzędem modelu. Wydawać by się mogło, że im więcej uwzględnimy poprzednich próbek, tym lepsze dopasowanie uzyskamy. Tak jednak nie jest. Ponieważ teoretyczne widmo procesu AR posiada maksima zależne od liczby użytych współczynników, modele o zbyt wysokich rzędach mają tendencję do generowania fałszywych maksimów w estymowanym widmie. Jeśli nie wiemy ilu składowych oczekujemy w naszym widmie, do oszacowania optymalnego rzędu modelu możemy zastosować jedno z kryteriów statystycznych, dostępnych w literaturze. Kryteria takie przeważnie mają dwie składowe: człon „nagradzający” za coraz „ściślejsze” dopasowanie wraz z rosnącym rzędem modelu oraz człon „karzący” za nadmierny wzrost rzędu. Szukamy wtedy minimum funkcji kryterium policzonej dla pewnego zakresu rzędów i tak wybraną wartość stosujemy potem w obliczeniach.
Jednym z popularnych kryteriów jest kryterium Akaikego (Hirotugu Akaike — matematyk japoński). Jest to funkcja:
gdzie:
N — liczba próbek w analizowanym sygnale, k — liczba kanałów.
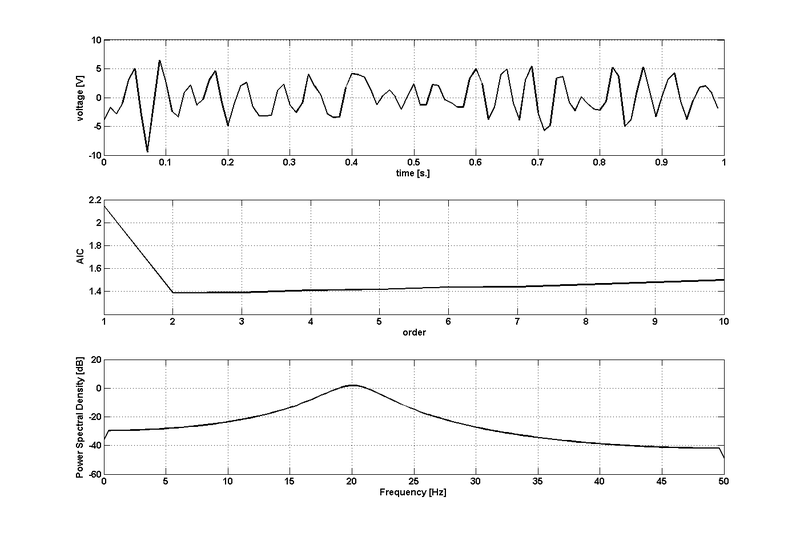
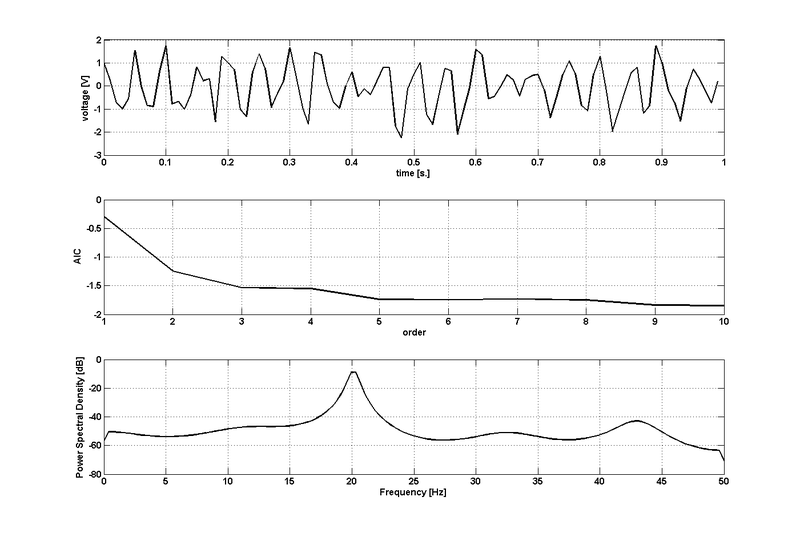
Logarytm wyznacznika macierzy wariancji szumów jest coraz bardziej ujemny, bo dopasowanie się polepsza i elementy macierzy V maleją. Funkcją kary jest tu 2pk2/N — funkcja liniowa rosnąca (od p). Szukamy pierwszego istotnego minimum krzywej opisywanej tą funkcją. W praktyce analizy EEG najczęściej stosuje się rzędy w zakresie od 4 do 9. Poniższe rysunki ilustrują możliwe sytuacje:
Sygnały wielokanałowe
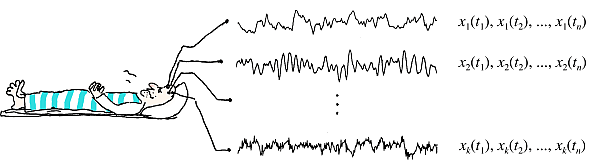
Sygnały wielokanałowe to zbiory danych, w których podczas jednej sesji zapisu zbieramy wartości wielu sygnałów w tych samych chwilach czasu. Zapisy EEG z wielu elektrod są oczywiście zapisami wielokanałowymi. Ważna jest tu jednoczesność rejestracji wielkości powiązanych ze sobą.
Przykładem danych wielokanałowych jest zapis EEG z wielu elektrod.
W przypadku wielokanałowego modelu w wyżej wypisanych wzorach opisujących model AR musimy dokonać pewnych modyfikacji. Jeśli zbieramy jednocześnie k sygnałów (kanałów), to X(t) jest w rzeczywistości wektorem k-wierszowym [X1(t), X2(t),..., Xk(t)]T, współczynniki modelu są (każdy z nich) macierzami rozmiaru k×k; wartości szumu są inne w każdym sygnale więc E(t) jest również wektorem [E1(t), E2(t),..., Ek(t)]T.
Po zaaplikowaniu transformacji Z i przejściu do dziedziny częstości, każda z uzyskanych transformat jest również albo wektorem k-wierszowym (X(f), E(f)) albo macierzą k×k (A(f), H(f)).
Gęstość widmowa mocy jest w tym przypadku dana jako (znak + oznacza tu transpozycję macierzy połączoną ze sprzężeniem zespolonym jej elementów):
Skorzystaliśmy tu z wiadomości, że widmo procesu czysto losowego E(f) jest funkcją stałą, a po wymnożeniu E(f)E+(f) dostajemy macierz wariancji szumów V (rozmiaru k×k), niezależną od częstości.
Z powyższego wzoru widać, że funkcja gęstości widmowej mocy jest macierzą rozmiaru k×k. Jej diagonalne elementy zawierają tzw. widma własne (auto-widma) każdego z sygnałów składowych, a elementy pozadiagonalne widma wzajemne (kross-widma).
Widzimy więc, że w przypadku analizy danych wielokanałowych mamy nie tylko wielkości opisujące każdy kanał osobno, ale również wielkości mówiące o informacji zawartej w zależnościach istniejących pomiędzy kanałami.
Widmo wzajemne opisuje istnienie spójnej zależności między dwoma sygnałami dla danej częstości. Jego moduł mówi nam o tym jak silna jest ta zależność, a faza mówi o wzajemnym przesunięciu fazowym składowych o danej częstości w każdym z dwóch sygnałów. Jeśli oba sygnały zawierają daną częstość, ale faza wzajemna tych składowych zmienia się, to widmo wzajemne będzie mieć wartość niską. Aby mieć wygodniejsze narzędzie porównawcze wprowadza się znormalizowaną wersję widma wzajemnego zwane koherencją (zwyczajną):
Moduł koherencji zawiera się w przedziale [0,1], co znacznie ułatwia porównywanie wyników.
Miary cząstkowe
W przypadku, gdy nasz zbiór danych składa się z dwóch kanałów, interpretacja koherencji jest w zasadzie jednoznaczna. Wydawać by się mogło, że jeśli będziemy ich używać do badania układów trzy- i więcej-kanałowych, to poza większą ilością obliczeń sytuacja ideowo nie będzie się różnić. Niestety, wraz ze wzrostem liczby kanałów sytuacja ulega zmianie.
Już w sytuacji trzech kanałów możemy napotkać tzw. wspólne źródło: kanał będący źródłem sygnału, który pojawia się w pozostałych kanałach (jak ta sama audycja u dwóch słuchaczy radia w innych miastach). Wtedy wartości koherencji nawet pomiędzy kanałami-odbiorcami sygnału będą wskazywać na istnienie związku między nimi, chociaż kanały te mogą nie być w żaden inny sposób ze sobą związane.
Aby móc łatwiej odróżnić taką sytuację dobrze byłoby umieć jakoś „odjąć” wpływ kanału-źródła na pozostałe. Czynność taka nazywa się w literaturze parcjalizacją względem danego kanału.
W ogólności mamy do dyspozycji funkcję koherencji cząstkowej, która zachowuje się podobnie do koherencji zwyczajnej, ale pokazuje związek między kanałami po odjęciu wszystkich kombinacji liniowych pozostałych kanałów. Zdefiniowana jest ona następująco:
We wzorze tym Mij jest minorem macierzy widmowej S, czyli wyznacznikiem macierzy S w której usunięto i-ty wiersz i j-tą kolumnę. Można tę definicję przekształcić do łatwiejszej do zastosowania postaci z użyciem elementów macierzy odwrotnej S−1. Jeśli dij(f) = [S−1]ij(f), mamy:
Tak więc miary cząstkowe muszą operować na więcej niż dwóch kanałach jednocześnie. Dzięki zastosowaniu wielokanałowego modelu AR założenie to jest spełnione i możemy w prosty sposób policzyć zarówno koherencje zwyczajne jak i cząstkowe dla dowolnej liczby kanałów w zestawie.
Ćwiczenia
W tekście ćwiczeń używać będziemy następujących założeń: posiadamy k kanałów danych, używamy modelu AR rzędu p, częstość próbkowania danych wynosi fs. W każdym kanale zebrano N próbek danych.
Aby ułatwić zapoznanie się z parametrycznymi metodami analizy widmowej, a nie rozpraszać uwagi na dopasowywanie współczynników modelu, przygotowana została biblioteka procedur (w języku Python) estymacji współczynników wielokanałowego modelu AR dla posiadanych danych. Aby jej użyć musimy napisać: import mtmvar
W zaimportowanym module mamy do dyspozycji funkcję mult_AR, która oczekuje parametrów:
- macierzy danych o wymiarach (k, N);
- wybranego rzędu modelu;
- numeru metody liczenia współczynników (aktualnie należy wybrać zawsze liczbę 1).
Funkcja zwraca krotkę zawierającą dwa obiekty:
- macierz policzonych współczynników, rozmiaru (p, k, k) — czyli p współczynników macierzowych rozmiaru k×k;
- macierz wariancji szumów V, rozmiaru (k, k) — patrz równanie (Equation 8).
Uwaga: macierz danych wejściowych musi mieć zawsze rozmiar (k,N), nawet jeśli k=1 (możemy ją wtedy uzyskać z pojedynczego wektora dane funkcją numpy.reshape(dane,(1,-1))).
Kilka słów o transformacji Z
Dla skończonego ciągu współczynników A(0), A(1), ..., A(p) ich transformata Z może być obliczona następująco:
Aby obliczyć wartość transformaty dla konkretnej częstości f musimy w powyższym wzorze dokonać podstawienia
gdzie Δt = 1 / fs.
Uwaga: procedura mult_AR zwraca współczynniki od A(1) do A(p) jak dla równania (Equation 3). Aby mieć zgodność z równaniem (Equation 4) musimy założyć A(0) = 1 oraz zmienić znak pozostałych współczynników na przeciwny.
Ćwiczenie 1
Z danych EEG zebranych na zajęciach dotyczących EEG spoczynkowego wyodrębnij jeden kanał. Wytnij z niego sygnał o długości 1000 próbek. Przefiltruj wycięty sygnał filtrem górnoprzepustowym (np. Butterwortha) o częstości odcięcia 1 Hz.
Oblicz współczynniki modelu AR dla wyciętego sygnału dla rzędów od 1 do 5. Zobacz również jak ze wzrostem rzędu modelu zmienia się macierz wariancji szumu.
Powtórz to samo dla sygnału w postaci pojedynczego sinusa oraz dla szumu.
Napisz funkcję liczącą kryterium Akaikego dla posiadanych danych dla zakresu rzędów 1-20. Funkcja powinna działać dla dowolnej liczby kanałów. Następnie napisz procedurę rysującą policzone kryterium tak, aby można było ocenić wizualnie jego przebieg i wybrać optymalny rząd modelu AR.
Ćwiczenie 2
Napisz funkcję obliczającą macierze A(f) i H(f) z równań (Equation 4) i (Equation 5) dla wybranego zestawu częstości z zakresu f0-fmax. Wykorzystaj tutaj równanie (Equation 12). Funkcja ma działać dla danych wielokanałowych (no i oczywiście jednokanałowych jako przypadek szczególny), tzn. jej argumentami powinny być: macierz zawierająca sygnał i rząd modelu.
Stosując napisaną funkcję oraz równanie (Equation 8) oblicz macierz gęstości widmowej mocy w zakresie częstości od 0 Hz do częstości Nyquista dla danych z poprzedniego ćwiczenia (z użyciem optymalnego rzędu modelu AR). Narysuj wykresy widm własnych i wzajemnych.
Ćwiczenie 3
- Wygeneruj dwa sygnały sinusoidalne o długości 1000 próbek każdy, o tej samej częstości 32 Hz i częstości próbkowania 128 Hz, ale różnych fazach początkowych.
- Pierwszy sygnał powinien mieć fazę początkową równą 0, drugi sygnał sinusoidalny powinien mieć fazę początkową równą π/4.
- Do drugiego z sygnałów dodaj małą (o amplitudzie ok 0,2 amplitudy sinusoidy) składową losową (czyli dodatkowy niezależny szum biały) o średniej 0.
- Z tak otrzymanych sygnałów utwórz jeden sygnał dwukanałowy (macierz o rozmiarze (2,1000)).
Podobnie jak poprzednio, ustal optymalny rząd modelu AR (tym razem dwukanałowego) i oblicz macierz gęstości widmowej mocy. Oblicz koherencje między tymi sygnałami. Narysuj moduł i fazę koherencji C12 i C21.
Zmień fazę początkową drugiego sygnału. Jak zmienia się funkcja koherencji?
Ćwiczenie 4
Wygeneruj układ trzech sygnałów w następujący sposób:
- jako pierwszego kanału użyj sygnału z ćwiczenia 1;
- sygnał_w_drugim_kanale(t) = 0,4 * sygnał_z_pierwszego_kanału(t−1) + szum1;
- sygnał_w_trzecim_kanale(t) = 0,3 * sygnał_z_pierwszego_kanału(t−2) + szum2.
Oblicz macierz koherencji zwyczajnych dla tego układu i na ich podstawie wyznacz zależności między kanałami. Powtórz to samo dla koherencji cząstkowych.
Wygeneruj zestaw danych jak poprzednio używając w kanale 1 sygnału z ćwiczenia 1. Powtórz obliczenia i porównaj wyniki.
Wyniki wszystkich obliczeń przedstaw na rysunkach.
Ćwiczenie 5
Z danych zawierających spoczynkowe EEG wytnij dwa fragmenty: zawierający i nie zawierający czynności alfa. Fragmenty powinny mieć cztery wybrane kanały danych (dwa z tyłu i dwa z przodu głowy, na przykład O1, O2, F3, F4) oraz długość ok. 500 próbek.
Dopasuj czterokanałowe modele AR do wyciętych fragmentów danych. Oblicz macierze gęstości widmowej mocy, koherencji zwyczajnych i koherencji cząstkowych dla obu fragmentów. Narysuj wykresy otrzymanych funkcji.