WnioskowanieStatystyczne/Bootstrap
Wnioskowanie_Statystyczne_-_wykład
Bootstrap
W poprzednim rozdziale zapoznaliśmy się z efektywnymi metodami oceny złożonych prawdopodobieństw w sytuacji, gdy znamy model rządzący zjawiskiem. Aby ocenić "prawdziwy" rozrzut badanej wielkości, generowaliśmy wiele powtórzeń tego samego eksperymentu. Rozkład wyników w tym zestawie danych (czyli próbie wylosowanej z populacji wszystkich możliwych wyników) przybliżał rozkład prawdopodobieństwa badanej wielkości — na przykład liczby wygranych gier. Dokładny rozkład prawdopodobieństwa uzyskalibyśmy dla nieskończonej liczby powtórzeń eksperymentu — mówimy, że populacja wyników tworzy zbiór nieskończony. Czasami mamy też do czynienia z próbą reprezentującą skończoną populację wyników, jak na przykład przy przewidywaniu wyników wyborów: kompletną populację stanowią wtedy opinie wszystkich obywateli uprawnionych do głosowania.
Niezależnie od tego, czy populacja (czyli przestrzeń możliwych wyników) jest skończona czy nie, nie wszystkie problemy daje się modelować w tak prostych kategoriach. Zwykle jest wręcz odwrotnie — dane, które mamy analizować, są jedyną dostępną informacją o całym badanym zjawisku. Co robić w takiej sytuacji? Jak na podstawie kilku czy kilkudziesięciu wylosowanych liczb określić np. rozrzut wartości średniej, skoro mamy tylko jedną próbę, z której ją (wartość średnią) wyliczamy? Oczywiście najlepiej byłoby powtórzyć eksperyment i uzyskać więcej danych, ale może się to okazać zbyt drogie lub wręcz niemożliwe. Co wtedy?
A może z tego jednego zestawu danych (próby) wygenerować inne próby, które zastąpią niezależne losowania z tej samej populacji lub powtarzanie eksperymentu? Pomysł ten przypomina opowieści barona von Münchhausena o tym, jak "wydobył się z bagna, ciągnąc się z całej siły za włosy" (za Słownikiem mitów i tradycji kultury Władysława Kopalińskiego) — stąd (pośrednio) nazwa bootstrap.[1] Idea tej metody jest niezmiernie prosta:
Jeśli nie możemy wylosować więcej prób z populacji, losujemy ze zwracaniem próby z danych, którymi dysponujemy.
Wróćmy do przykładu z poprzedniego rozdziału, czyli gry w "pięć rzutów kostką". Dzięki dokładnemu modelowi całej gry mogliśmy tanim kosztem symulować właściwie dowolną liczbę powtórzeń, dzięki czemu określiliśmy nie tylko prawdopodobieństwo wygranej w pojedynczej grze, ale też ryzyko, jaki podejmujemy decydując się na sto gier. A gdyby wewnętrzne mechanizmy gry nie były znane, albo były tak skomplikowane, że nie dało by się ich zamodelować nawet językiem prawdopodobieństwa? Wyobraźmy sobie, że:
jedyną informacją o procesie jest 18 wygranych w stu grach.
Co można w tej sytuacji powiedzieć o szansach? Cóż, możemy ocenić prawdopodobieństwo wygranej na około 18.
"około"?
Żeby oszacować rozrzut tej wielkości, trzeba by mieć wyniki przynajmniej kilkuset takich serii. Albo... wyciągnąć się z bagna za włosy, czyli wygenerować setki serii z tej jednej serii!
Jak?
Jeśli się nad tym zastanowimy, poznamy od razu ograniczenia metody: otóż zakładamy, że próbka zawiera informację reprezentatywną dla całej populacji, w tym przypadku wszystkich możliwych wyników stu gier. W pewnym sensie jest to truizm, bo przecież i tak nie mamy dostępu do innych informacji niż zawarte w próbie. Wynika stąd, że proporcję wygranych w tej próbie (0,18) musimy uznać za prawdopodobieństwo wygranej w jednej grze. Repróbkowanie będzie polegało na losowaniu ze zwracaniem stu elementów spośród 18 jedynek i 82 zer. Każdy wylosowany w ten sposób zestaw będziemy traktować jak niezależną próbę: obliczamy dla tych danych interesującą nas wielkość — w tym przypadku po prostu sumę elementów, odpowiadającą liczbie wygranych. Możemy to zaprogramować np. wedle algorytmu z tabeli %i 1. W pakietach obliczeniowych coraz częściej pojawiają się gotowe funkcje realizujące podstawowy algorytm bootstrapu — warto to sprawdzić, zanim zabierzemy się do pisania pętli.
jedynki = 0
powtarzaj 100 razy:
wylosuj x od 1 do 100
jeśli x mniejszy lub równy od 18
jedynki = jedynki + 1
wypisz jedynki
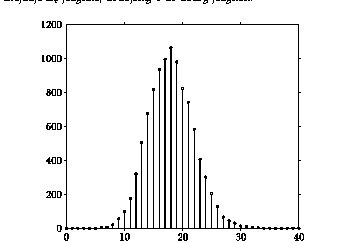
Średnia tych wyników powinna oczywiście dążyć do 18 — niestety nie mamy szansy przybliżyć się na podstawie tej jednej próby do "prawdziwej" średniej, którą uzyskalibyśmy przy większej liczbie powtórzeń symulacji lub "prawdziwych" eksperymentów. Ale możemy odzyskać inną bardzo ważną informację — rozrzut wyników. Spróbujmy powórzyć 10 tysięcy takich losowań "z próby" według algorytmu z tabeli 16, i obejrzeć ich rozkład na rysunku %i 1.
Działa!!!
Otrzymany rozkład jest bardzo podobny do rozkładu dziesięciu tysięcy "prawdziwych" symulacji (rys. %i 1)! Szerokość (i kształt) rozkładu są niemal identyczne, przesunięte jest tylko maksimum — w tym przypadku wypada dla wartości 18, a nie jak w przypadku "prawdziwych" symulacji w okolicach najbardziej prawdopodobnej wartości (około 20). Ale na to już nie ma rady, liczba sukcesów w próbie, na której przeprowadzaliśmy repróbkowanie, wynosiła właśnie tyle, i dane te nie są wystarczające, aby ocenić, czy wynik ten leży "na prawo czy na lewo" od dokładnej wartości prawdopodobieństwa. Za to rozrzut udało się odtworzyć wręcz doskonale!
Scyzoryk (jacknife )
Jest to metoda analogiczna do bootstrapu, w ktorej powtórzenia generowane są przez usuwanie z próby kolejno po jednym elemencie. W porównaniu z bootstrapem daje w niektórych przypadkach oszczędność ilości obliczeń, ale ze względu na generowanie prób o mniejszej liczebności niż oryginalna wymaga stosowania mniej intuicyjnych wzorów.
<references>
- ↑ Bootstrap to po angielsku "pętla ze skóry lub materiału przyszyta z boku lub od góry tylnej strony buta dla ułatwienia jego wciągania"(za The American Heritage Dictionary of the English Language). Bradley Efron, który zaproponował tę technikę, pisze o nazwie: "The name bootstrap, which is derived from the old saying about pulling yourself up by your own bootstraps, reflects the fact that the one available sample gives rise to many others" (w Diaconis, P. & Efron, B. (May 1983). "Computer-intensive methods in statistics". Scientific American: 116–130.). W książce (strona 5) precyzuje explicite, że powiedzenie to wedle ogólnego przekonania wywodzi się właśnie z opowieści barona von Münchhausena. Jednak Kopaliński w odniesieniu do opowieści barona wspomina zdecydowanie o wyciąganiu z bagna za włosy, a nie za buty. W związku z tymi niezgodnościami, jak również z faktem, że ten sam termin używany od dość dawna w odniesieniu do procedur komputerowych nie doczekał się polskiego tłumaczenia, najsensowniejszym wydaje się pozostawienie oryginalnego brzmienia. Cz. Domański i K. Pruska podają "metody sznurowadłowe" jako odpowiednik terminu "metody bootstrapowe".