WnioskowanieStatystyczne/Elementy statystyki wielowymiarowej
Wnioskowanie_Statystyczne_-_wykład
Spis treści
Elementy statystyki wielowymiarowej
Przypomnijmy najpierw pojęcia
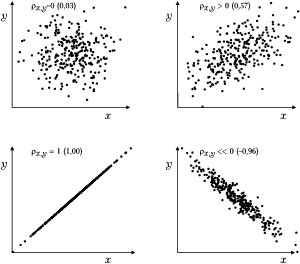
Kowariancja i współczynnik korelacji
Miarą związku między zmiennymi [math]x[/math] i [math]y[/math] jest kowariancja
[math] \sigma_{x, y} = E\left( (x-\mu_{x})(y-\mu_{y})\right) [/math]
lub unormowany do jedności współczynnik korelacji zmiennych [math]x[/math] i [math]y[/math]:
[math] \rho_{x, y}= \frac{\sigma_{x, y}}{\sigma_x \sigma_y}= \frac{E\left( \left(x-\mu_{x})(y-\mu_{y}\right)\right)} {\sqrt{E\left( (x-\mu_{x})^2\right) E\left( (y-\mu_{y})^2\right)}}, [/math]
gdzie [math]\mu_x[/math] i [math]\mu_y[/math] to odpowiednio wartości oczekiwane zmiennych [math]x[/math] i [math]y[/math]. Jeśli zmienne [math]x[/math] i [math]y[/math] związane są deterministyczną zależnością liniową (typu [math]y=c_1 x+c_2[/math]), to ich korelacja wynosi [math]1[/math] (lub [math]-1[/math], jeśli [math]c_1\lt 0[/math]). Jeśli wzrostowi zmiennej [math]x[/math] towarzyszy statystycznie wzrost zmiennej [math]y[/math], to ich korelacja jest dodatnia (pomiędzy [math]0[/math] a [math]1[/math]). Dla zmiennych niezależnych korelacja wynosi [math]0[/math].
Macierz kowariancji
[math] C=E[(x-\mu )(x-\mu )^{T}], \qquad \\ c_{ij}=E[(x_{i}-\mu_{i})(x_{j}-\mu _{j})] [/math]
dla dwóch wymiarów: [math]x=(x_{1,}x_{2})[/math] i [math]\mu =(\mu _{1}, \mu _{2})[/math]
[math] C=E\left[ \left(\begin{matrix}{x_{1}-\mu _{1}}\\ {x_{2}-\mu _{2}} \end{matrix} \right) \left( x_{1}-\mu_{1},x_{2}-\mu _{2}\right) \right] = [/math]
[math] \left[ \begin{matrix} E\left[ \left( x_{1}-\mu _{1}\right) ^{2}\right] & E\left[ \left( x_{1}-\mu _{1}\right) \left( x_{2}-\mu _{2}\right) \right] \\ E\left[ \left( x_{2}-\mu _{2}\right) \left( x_{1}-\mu _{1}\right) \right] & E \left[ \left( x_{2}-\mu _{2}\right) ^{2}\right] \end{matrix} \right] = [/math]
[math]
\left[
\begin{matrix}
\sigma _{1}^{2} & \sigma _{12} \\
\sigma _{21} & \sigma _{2}^{2}
\end{matrix}
\right]
[/math]
ogólnie
[math]
S=\left[
\begin{matrix}
\upsilon ar(x_{1}) & co\upsilon (x_{1},x_{2}) & ... & co\upsilon
(x_{1},x_{k}) \\
co\upsilon (x_{2},x_{1}) & \upsilon ar(x_{2}) & ... & co\upsilon
(x_{2},x_{k}) \\
... & ... & ... & ... \\
co\upsilon \left( x_{k},x_{1}\right) & co\upsilon (x_{k},x_{2}) & ... &
\upsilon ar(x_{k})
\end{matrix}
\right]
[/math]
Analiza wariancji wielu zmiennych (Multivariate ANalysis of VAriance — MANOVA)
Wcześniej rozpatrywaliśmy podział na grupy pomiarów opisanych jedną zmienną (analiza wariancji jednej zmiennej). Jeśli zmienna losowa [math]X[/math] jest opisana wektorem ([math]x_{1},...,x_{k})[/math], wartość wektorem o tym samym wymiarze: ([math] \mu _{1},...,\mu _{k})[/math], to w miejsce wariancji mamy do czynienia z macierzą kowariancji:
[math]
S=\left[
\begin{matrix}
\upsilon ar(x_{1}) & co\upsilon (x_{1},x_{2}) & ... & co\upsilon
(x_{1},x_{k}) \\
co\upsilon (x_{2},x_{1}) & \upsilon ar(x_{2}) & ... & co\upsilon
(x_{2},x_{k}) \\
... & ... & ... & ... \\
co\upsilon \left( x_{k},x_{1}\right) & co\upsilon (x_{k},x_{2}) & ... &
\upsilon ar(x_{k})
\end{matrix}
\right]
[/math]
gdzie:
[math]
\upsilon ar(x_{i})=\sigma _{x_{i}}=E((x_{i}-\mu _{i})^{2})
[/math]
[math]
co\upsilon (x_{i},x_{k})=\sigma _{x_{i},x_{k}}=E((x_{i}-\mu _{i})(x_{k}-\mu
_{k}))
[/math]
Zakladamy, że dane pochodzą z wielowymiarowego rozkładu normalnego, opisanego macierzą kowariancji [math]S[/math]
[math]
\Phi (X)=\frac{1}{\sqrt{(2\pi )^{k}}\sqrt{\left| S\right| }}e^{-\frac{(X-\mu
)^{\prime }S^{-1}(X-\mu )}{2}}
[/math]
Jeśli [math]X[/math] pochodzą z próby
podzielonej na grupy, to podobnie jak w ANOVA możemy
skonstruować macierze wariancji wewnątrzgrupowych i międzygrupowych i
dowieść, że [math]S=S_{wew}+S_{pom}[/math].
Testujemy hipotezę o równości średnich w grupach
[math] H_0: \mu_1 = \mu_2 = \cdots = \mu_k [/math]
Jako statystykę testową możemy wybrać np. iloraz wyznaczników macierzy [math]S_{wew}[/math] i [math]S[/math], który podlega rozkładowi [math]\Lambda [/math] Wilksa:
[math]
\Lambda =\frac{\left| S_{wew}\right| }{\left| S\right| }=\frac{\left| S_{wew}\right| }{\left| S_{wew}+S_{pom}\right| }
[/math]
Uczenie (maszynowe, ML) nienadzorowane (unsupervised learning)
Analiza składowych głównych (Principal Components Analysis, PCA)
Jeśli zmienne są bardzo silnie skorelowane, mamy do czynienia z redundancją. Możemy ją zmniejszyć, redukując wymiar danych. W tym celu macierz kowariancji
[math]
S=\left[
\begin{matrix}
\upsilon ar(x_{1}) & co\upsilon (x_{1},x_{2}) & ... & co\upsilon
(x_{1},x_{k}) \\
co\upsilon (x_{2},x_{1}) & \upsilon ar(x_{2}) & ... & co\upsilon
(x_{2},x_{k}) \\
... & ... & ... & ... \\
co\upsilon \left( x_{k},x_{1}\right) & co\upsilon (x_{k},x_{2}) & ... &
\upsilon ar(x_{k})
\end{matrix}
\right]
[/math]
przedstawiamy w postaci diagonalnej
[math]
S=\left[
\begin{matrix}
r_{11} & r_{12} & ... & r_{1k} \\
r_{21} & r_{22} & ... & r_{2k} \\
... & ... & ... & ... \\
r_{k1} & r_{k2} & ... & r_{kk}
\end{matrix}
\right] \left[
\begin{matrix}
\lambda _{1} & 0 & ... & 0 \\
0 & \lambda _{2} & ... & 0 \\
... & ... & ... & ... \\
0 & 0 & ... & \lambda _{k}
\end{matrix}
\right] \left[
\begin{matrix}
r_{11} & r_{21} & ... & r_{k1} \\
r_{12} & r_{22} & ... & r_{k2} \\
... & ... & ... & ... \\
r_{1k} & r_{2k} & ... & r_{kk}
\end{matrix}
\right]
[/math]
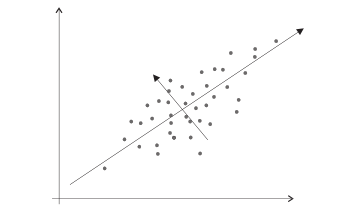
Wielkości [math]\lambda _{i}[/math] są rozwiązaniami równania
[math]\left| S-\lambda I\right| =0,[/math] a wektor [math]r_{i}[/math]
osiami nowego układu współrzędnych. Składowe PCA są
liniowymi kombinacjami obserwowanych zmiennych.
Analiza skupień — Cluster Analysis
Wejściem dla tej klasy procedury są nieoznaczone dane, a wyjściem ich podział na grupy. Obecnie metody tego typu określamy czasem jako "unsupervised learning".
Metody polegające na kolejnym łączeniu punktów
Startujemy z N klastrów jednopunktowych, w każdym kroku łączymy najbliższe. Wynikiem działania jest drzewo łączenia, na którym sami musimy wybrać ilość klastrów. Wynik zależy silnie od przyjętych definicji odległości między klastrami oraz definicji odległości między punktami.
Odległości między punktami:
- Odległość Euklidesowa [math]d(x,y)=\sqrt{\underset{i=1}{\overset{k}{\sum }}(x_{i}-y_{i})^{2}}[/math] (czuła na różne skale cech).
- Odległość korelacyjna [math]d(x,y)=1-\rho (x,y),[/math] gdzie [math]\rho (x,y)=\frac{\underset{i=1}{\overset{k}{\sum }}(x-\overline{x})(y- \overline{y})}{\sigma _{x}\sigma _{y}} [/math] (znormalizowana do przedziału (0,2), mniejsza im lepiej skorelowane punkty).
Odległości między klastrami:
- Najbliższego sąsiada (single linkage) - odległość między dwoma najbliższymi elementami klastrów A i B: [math]d(A,B)=\min_{x,y}d(x,y),\ \ \ \ \ x\in A,\ y\in B[/math]
- (complete linkage ) - odległość między dwoma najbliższymi elementami klastrów A i B: [math]d(A,B)=\max_{x,y}d(x,y),\ \ \ \ \ x\in A,\ y\in B [/math]
- (centroid) - odległość między środkami klastrów,
- (average) - średnia odległości, itd...
Metoda K–średnich (K – means )
Wybieramy ilość klastrów, podział dokonywany jest w iteracyjnej procedurze dążącej do minimalizacji stosunku wariancji pomiędzy klastrami do wariancji wewnątrz klastrów — niejako [math]ANOVA[/math] bez ustalonego wstępnie przyporządkowania, maksimum [math] F[/math] poszukiwane drogą przemieszczania elementów między klastrami.