WnioskowanieStatystyczne/Test t
Wnioskowanie_Statystyczne_-_wykład
Rozkład [math]t[/math] Studenta
W poprzednim rozdziale rozważaliśmy rzadki w praktyce przypadek, w którym dokładną postać rozkładu — włącznie z parametrami, czyli wartością oczekiwaną i wariancją — któremu podlega statystyka testowa, mogliśmy uznać za znaną.[1] W praktyce częściej zdarza się sytuacja, w której informacje musimy czerpać bezpośrednio z testowanych danych. Załóżmy, że nie mamy możliwości niezależnej oceny rozrzutu prawidłowych wyników, ale za to każdy student przynosi wyniki kilku ([math]N[/math]) pomiarów. Na podstawie tej próby możemy estymować wariancję wyników dla danego układu, czyli populacji wszystkich możliwych wyników. Według wzorów na estymator wartości oczekiwanej (wartość średnią) i estymator wariancji wartości średniej jej estymatą będzie:
[math] { s_{x}^{2}=\frac{1}{N-1}\underset{i=1}{\overset{N}{\sum }}(x_{i}- \overline{x})^{2}\ } [/math]
a estymatą wariancji wartości średniej próby
[math] { s_{\overline{x}}^{2}=\frac{1}{N(N-1)}\underset{i=1}{\overset{N}{\sum }}(x_{i}-\overline{x})^{2}\ }. [/math]
Jaką funkcję wybrać na statystykę testową? Tak jak poprzednio zakładamy, że wyniki pochodzą z rozkładu normalnego o średniej równej tablicowej wartości przyspieszenia ziemskiego (9,81), jednak nie znamy jego wariancji.
Jako miarę rozbieżności możemy wybrać ponownie różnicę między wartością oczekiwaną według hipotezy zerowej i wartością otrzymaną w wyniku eksperymentu (w tym przypadku weźmiemy średnią otrzymanych wyników), ale podzieloną tym razem przez estymowaną wariancję wartości średniej próby. W poprzednim przypadku wariancję populacji prawidłowo przeprowadzanych eksperymentów uznaliśmy za znaną, np. wyznaczoną w niezależnie przeprowadzonym eksperymencie. Tym razem wariancję będziemy estymować z tej samej próby, która podlega ocenie w przeprowadzanym teście.
Przypomnijmy, że gdy dysponujemy "prawdziwą" wartością wariancji, transformacja zmiennej losowej [math]x_i[/math] pochodzącej z rozkładu Gaussa o średniej [math]\mu[/math] i wariancji [math]\sigma^2[/math]
[math] \overline{x}\longrightarrow \frac {\overline{x} - \mu}{\sigma_{\overline{x}}} [/math]
daje zmienną ze standardowego rozkładu Gaussa o [math]\mu=0[/math] i [math]\sigma=1[/math]. Jednak jeśli w miejsce wariancji wartości średniej [math]\overline{x}[/math] wstawimy jej estymatę, dostaniemy zmienną [math]t[/math]:
Przy założeniu normalnego rozkładu populacji, z której losowano [math]x_i[/math], zmienna [math]t[/math] podlega[2] rozkładowi Studenta[3] o [math]f=(N-1)[/math] stopniach swobody[4]:
gdzie [math]\Gamma[/math] — funkcja Eulera; [math]\Gamma(x+1)=\int_0^\infty t^xe^{-t}dt[/math]; [math]\Gamma(n+1)=n![/math] dla [math]n=1,2,\ldots[/math]
Cóż, nie udało się "dojść" do rozkładu Gaussa, ale rozkład dany równaniem (2) możemy równie dobrze wykorzystywać do weryfikacji hipotez, używając wciąż tego samego schematu. Statystykę testową będziemy obliczać według wzoru (1), a obszar akceptacji testu dla tej statystyki będziemy wyznaczać z rozkładu danego równaniem (2).
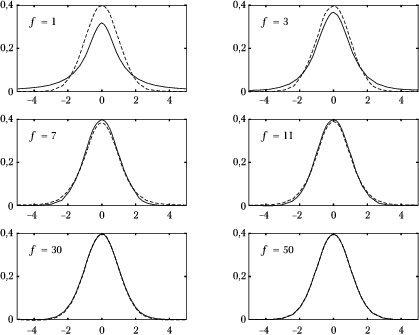
Mimo zupełnie różnego wzoru, rozkład Studenta dla dużej liczby stopni swobody [math]f[/math] dąży asymptotycznie do rozkładu Gaussa; zbieżność tę ilustruje rysunek (1).
Test [math]t[/math] (Studenta) różnicy średnich
W praktyce najczęściej występuje sytuacja, w której nie znamy żadnego z parametrów rozkładów określających hipotezę zerową. Wprowadzony w poprzednim rozdziale rozkład Studenta najczęściej wykorzystujemy w sytuacji, gdy mamy dwie próby (grupy wyników) i pytamy, czy pochodzą z tej samej populacji. Wartości średnie prób oznaczymy [math]\overline{x}_{1}[/math] i [math]\overline{x}_{2}[/math], a ich wariancje, zgodnie ze wzorem na estymator wariancji, estymujemy przez
[math] s_{x_i}^2= \frac{1}{(N_i-1)}\sum\limits_{j=1}^{N_i} (x_{j}-\overline{x}_{i})^{2} [/math]
dla [math]i=1[/math] lub [math]2[/math]. Estymatą wariancji populacji [math]s^2[/math] (jeśli próby pochodzą z jednej populacji) będzie suma kwadratów odchyleń od średniej w każdej próbie, czyli [math](N_i-1)s_{x_i}^2[/math], podzielona przez liczbę stopni swobody, czyli sumę liczb elementów w obu próbach minus dwa, gdyż wyliczamy dwie średnie w próbach:
[math] s^{2}=\frac{(N_1-1)s_{x_{1}}^{2}+(N_2-1)s_{x_{2}}^{2}}{N_{1}+N_{2}-2}. [/math]
Przy założeniu losowania obu grup z tej samej populacji, wariancje średnich będą wynosić [math]s_{\overline{x}_{i}}^{2}=\frac{s^{2}}{N_{i}}[/math] (według wzoru na estymator wariancji wartości średniej), więc estymatą wariancji różnicy wartości średnich będzie suma tych wariancji:
[math] s_{\Delta }^{2}=s_{\overline{x}_{1}}^{2}+s_{\overline{x}_{2}}^{2} =\frac 1{N_1} s_1^2+\frac 1{N_2}s_2^2 =\frac{N_{1}+N_{2}}{N_{1}N_{2}}s^{2}. [/math]
Wielkość
podlega rozkładowi Studenta z liczbą stopni swobody [math]f=N_{1}+N_{2}-2[/math].
Ta właśnie statystyka liczona jest w popularnym teście różnicy wartości średnich dwóch grup ([math]\overline{x}_1[/math] i [math]\overline{x}_2[/math]). Do obliczania granic obszaru akceptacji użyjemy oczywiście wzoru (2)), któremu w świetle hipotezy zerowej podlega wielkość [math]t[/math] z równania (3).
Podobnie jak inne testy parametryczne[5], wyprowadzony powyżej test podlega zasadniczemu ograniczeniu. Otóż rozumowanie, które doprowadziło nas do wyprowadzenia postaci rozkładu statystyki testowej opiera się na założeniu, że zmienne pochodzą z populacji o rozkładzie gaussowskim. Jeśli nie jest ono spełnione,[6] różnica średnich nie będzie podlegać rozkładowi Studenta. Nawet jeśli równość ta nie jest spełniona, to według wzoru (3) większa wartość [math]t[/math] odpowiada większej różnicy średnich grup, niezależnie od rozkładu populacji, z której grupy pochodzą. Jednak dla innych niż gaussowski rozkładów zmiennych wejściowych nie możemy obliczać poziomów istotności według wzoru (2), który wyprowadzono w oparciu o założenie losowania prób z rozkładu normalnego. Jeśli założenia nie będą spełnione, otrzymamy nieprawdziwe wyniki. Obliczony w ten (błędny) sposób poziom istotności dla akceptacji hipotezy zerowej nie będzie odpowiadał rzeczywistości, co może prowadzić np. do odrzucenia zamiast przyjęcia hipotezy.
Jest to podstawowy problem, z którym stykamy się używając testów statystycznych opartych o założenie normalnego rozkładu populacji. Alternatywą są oczywiście opisane w części pierwszej testy permutacyjne, lub — pozostając w ramach statystyki klasycznej — testy nieparametryczne. Jednak jeśli założenie o normalności rozkładu jest spełnione (uzasadnione), test parametryczny oferuje większą moc (dzięki wykorzystaniu dodatkowej informacji o rozkładzie).
Przykład
Zastosujmy test [math]t[/math] do danych z przykladu — przypomnijmy:
liczby braków w kolejnych dniach przed remontem lini produkcyjnej wynosiły: 12, 9, 21, 14, 7 i 17, a po remoncie: 5, 9, 3, 11, 8, 19, 7, 5, 9, 12, 5, 11, 9, 6, 8, 17, 9 i 12. Pytamy, czy remont zmienił średnią ilość braków na dzień.
Przede wszystkim zastanówmy się, czy w ogóle możemy zastosować do tych danych test [math]t[/math]? Musielibyśmy wtedy przyjąć odpowiedzialność za założenie, że dane pochodzą z populacji o rozkładzie normalnym.[7] Jednak w tym przypadku trudno znaleźć a priori uzasadnienie dla takiego założenia, a samych danych mamy za mało, żeby zastosować np. sprawdzian proponowany w rozdziale o teście [math]\chi^2[/math] Pearsona. Tak więc w przypadku braku dodatkowych informacji należy stwierdzić, że nie ma wystarczającego uzasadnienia dla zastosowania testu [math]t[/math] i należy skorzystać np. z testu permutacyjnego lub nieparametrycznego testu Manna-Whitney'a-Wilcoxona, który również nie wymaga spełnienia założenia o normalności rozkładów.
Załóżmy jednak, że po przeprowadzeniu dodatkowych badań (tj. zebraniu większej ilości danych lub badaniach istoty samego procesu) uzyskaliśmy wyniki uzasadniające przyjęcie założenia o normalności.[8] Wtedy obliczona według wzoru (3). wartość statystyki [math]t[/math] wyniesie 2,0185. Porównywać ją będziemy z rozkładem [math]t[/math] (wzór (2)) dla 22 stopni swobody, gdyż mamy 6+18 liczb i dwa więzy (średnie w dwóch grupach). Wartość krytyczna poziomu istotności dla testu jednostronnego (testujemy hipotezę o zmniejszeniu liczby braków) wyniesie 2,8%, czyli na poziomie istotności 5% możemy odrzucić hipotezę o braku różnic między grupami, co sugeruje istotne zmniejszenie liczby braków po remoncie.
Zwróćmy uwagę, że zastosowany dla tych samych danych test permutacyjny dał tę samą odpowiedź, jednak przy większej wartości krytycznej poziomu istotności (3,8%). Świadczy to o większej mocy (por. rys 3 z poprzedniego rozdziału) testu ([math]t[/math]) opartego na dodatkowych założeniach, czyli wykorzystującego więcej informacji (znajomość postaci rozkładu).
<references>
- ↑ Założyliśmy postać rozkładu normalnego i oba określające go parametry — wariancję [math]\sigma^2[/math] i średnią [math]\mu[/math].
- ↑ Dowód tego faktu można znaleźć w książce "Probabilistyka. Rachunek Prawdopodobieństwa. Statystyka matematyczna. Procesy stochastyczne" Agnieszki i Edmunda Plucińskich.
- ↑ Rozkład ten wprowadził do statystyki w roku 1908 William S. Gosset] — chemik z browaru Guinessa, posługujący się pseudonimem "Student".
- ↑ Liczba stopni swobody to w skrócie liczba zmiennych niezależnych pomniejszona o liczbę wyznaczanych na ich podstawie wielkości; w tym przypadku mamy [math]N[/math] zmiennych i korzystamy z wyznaczonej na ich podstawie jednej wielkości — wartości średniej [math]\overline{x}[/math], czyli [math]f=N-1[/math].
- ↑ Czyli oparte na założeniu normalności rozkładu populacji, z których pochodzą badane próby.
- ↑ W tym przypadku dodatkowym wymogiem jest równość (w praktyce podobna wartość) wariancji obu prób — założyliśmy ją wyprowadzając statystykę testową.
- ↑ Oraz o równości wariancji, lecz w tym przypadku wydają się one wystarczająco podobne.
- ↑ W przypadku danych określających liczby zliczeń bardziej uzasadnione będzie zwykle założenie rozkładu Poissona. Jednak dla dużych wartości parametru [math]\lambda[/math] rozkład Poissona przechodzi w rozkład Gaussa — załóżmy, że mamy do czynienia właśnie z takim przypadkiem.