WnioskowanieStatystyczne/Twierdzenie Bayesa
Wnioskowanie_Statystyczne_-_wykład
Spis treści
Prawdopodobieństwo warunkowe i zdarzenia niezależne
Zapis [math]P(A\mid B)[/math] oznacza prawdopodobieństwo zdarzenia [math]A[/math] liczone w sytuacji, gdy mamy pewność wystąpienia zdarzenia [math]B[/math]. Odpowiada to w pewnym sensie wystąpieniu obydwu zdarzeń ([math]A\cap B[/math]), jednak prawdopodobieństwo tej sytuacji należy obliczać inaczej niż [math]P(A\cap B[/math]).
Przykład: Niech [math]A[/math] oznacza wyrzucenie szóstki, a [math]B[/math] — wyrzucenie parzystej liczby oczek w rzucie kostką. Wtedy [math]A\cap B[/math] oznacza wyrzucenie szóstki, [math]P(A\cap B)=\frac{1}{6}[/math]. Jednak jeśli bierzemy pod uwagę tylko te przypadki, w których wyrzucono parzystą liczbę oczek (2, 4 lub 6), to [math]P(A\mid B)=\frac{1}{3}[/math].
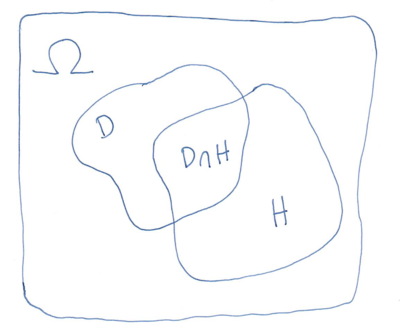
Rozważmy [math]P(A\mid\Omega)[/math]; dla dowolnego [math]A[/math]
mamy
- [math] P(A)=P(A\mid\Omega)=P(A\cap\Omega)[/math]
bo oczywiście [math]A\in\Omega[/math].
Rozbijając przestrzeń wszystkich możliwych zdarzeń [math]\Omega[/math] na część odpowiadającą zdarzeniu [math]B[/math] i pozostałą [math]\overline B[/math] ([math]\Omega=B\cup\overline{B}[/math]), dostajemy:
- [math] P(A)=P(A\mid\Omega)=\\ P\left(A\cap(B\cup\overline{B})\right)=\\ P\left((A\cap B)\cup(A\cap\overline{B})\right)=\\ P(A\cap B) + P(A\cap\overline{B})[/math]
czyli prawdopodobieństwo zdarzenia [math]A[/math] jest równe sumie
prawdopodobieństw zajścia [math]A[/math], jeśli zaszło również
[math]B[/math], oraz prawdopodobieństwa zajścia [math]A[/math], jeśli
[math]B[/math] nie zaszło. Jeśli wiemy, że zaszło zdarzenie
[math]B[/math] (wszak liczymy [math]P(\cdot\mid B)[/math]), to drugi
człon znika ([math]P(\overline{B})=0[/math]). Aby uzyskać wzór na
[math]P(A\mid B)[/math], pozostały człon musimy podzielić przez
[math]P(B)[/math] (aby dla [math]B=A[/math] było [math]P(A\mid
A)=1[/math])
- [math] P(A\mid B)=\frac{P(A\cap B)}{P(B)} [/math]
Jeśli wystąpienie zdarzenia [math]B[/math] nie ma żadnego wpływu na
prawdopodobieństwo wystąpienia zdarzenia [math]A[/math], czyli
[math]P(A\mid B)=P(A)[/math], to mówimy, że zdarzenia [math]A[/math] i
[math]B[/math] są niezależne. Z powyższego równania wynika, że dla zdarzeń niezależnych [math]A[/math] i [math]B[/math] zachodzić będzie
[math]
P(A\cap B)=P(A)P(B)
[/math]
W przykładzie z kostką:
- [math]P(\textrm{parzysta liczba oczek})=\frac{1}{2}[/math],
- [math]P(\mathrm{szóstka})=\frac{1}{6}[/math],
- [math]P(\mathrm{szóstka} | \textrm{parzysta liczba oczek}) = \dfrac{\frac16}{\frac12} = \frac13[/math].
Twierdzenie Bayesa
Twierdzenie Bayesa można wyprowadzić z elementarnych reguł prawdopodobieństwa, wychodząc z powyższej definicji prawdopodobieństwa warunkowego. Ponieważ interesuje nas głównie weryfikacja hipotez statystycznych, przekształćmy ten wzór, wstawiając od razu zamiast zdarzeń [math]A[/math] i [math]B[/math] hipotezę [math]H[/math] i dane [math]D[/math]. Wtedy [math]P(D\mid H)[/math] będzie prawdopodobieństwem wylosowania danych [math]D[/math] pod warunkiem, że prawdziwa jest hipoteza [math]H[/math]:
Analogicznie
[math] P(H\mid D) = \frac{P(H\cap D)}{P(D)} \Longrightarrow P(H\cap D)=P(H\mid D) P(D). [/math]
Ponieważ
[math]P(D\cap H)=P(H\cap D)[/math]
czyli
[math]P(D\mid H) P(H) = P(H\mid D) P(D)[/math]
dostajemy
Prawdopodobieństwo [math]P(D)[/math] uzyskania w doświadczeniu danych
[math]D[/math] trudno ocenić bezpośrednio, jeśli nie wiemy, czy
prawdziwa jest odnosząca się do nich hipoteza [math]H[/math]. W tej
sytuacji należy wziąć pod uwagę wszystkie możliwe hipotezy
[math]H_i[/math], tworzące kompletny, czyli pokrywający całą
przestrzeń [math]\Omega[/math]: [math]\sum_i H_i=\Omega[/math] zbiór
hipotez [math]H_i[/math] wykluczających się wzajemnie [math]\left(
P(H_i\cap H_j)=0 \right)[/math]. Wtedy
[math]
P(D)=P(D\cap\Omega)=\sum_i P(D\cap H_i).
[/math]
Korzystając z (1) dostajemy
[math]
P(D)=\sum_i P(D\mid H_i) P(H_i) \,\,\,\,\,\, (3)
[/math]
Wstawiając tę zależność do (2), i podstawiając za
[math]H[/math] jedną z możliwych [math]H_i[/math], dostajemy wzór
wyrażający twierdzenie Bayesa:
[math]
P(H_i\mid D)=\frac{P(D\mid H_i)P(H_i)}{\sum_j P(D\mid H_j)P(H_j)}.
[/math]
Prawdopodobieństwo hipotezy [math]H_i[/math] wyrażone jest przez:
- prawdopodobieństwo uzyskania w jej świetle danych [math]D[/math], czyli [math]P(D\mid H_i)[/math]
- stopień naszego zaufania do hipotezy [math]H_i[/math] (niezależny od eksperymentu, w którym uzyskaliśmy dane [math]D[/math]), czyli [math]P(H_i)[/math]
- całkowite prawdopodobieństwo uzyskania danych [math]D[/math] w świetle wszystkich możliwych hipotez [math]H_j[/math], czyli [math]\sum_j P(D\mid H_j)P(H_j)[/math]
Najbardziej bulwersujące jest tu [math]P(H_i)[/math], wyrażające naszą wiarę w hipotezę [math]H_i[/math] niezależną od danych [math]D[/math]. Wielkość tę określa się mianem prawdopodobieństwa "a priori", lub jak proponuje R. Nowak, "prawdopodobieństwem zaczątkowym" lub "zaczątkiem" . Dla odróżnienia od (szukanego) prawdopodobieństwa [math]P(H)[/math] oznaczmy zaczątek jako [math]P_0[/math]; wzór Bayesa przyjmie wtedy postać
Jeśli nie dysponujemy informacją o kompletnym zbiorze hipotez [math]H_i[/math], możemy badać stosunek prawdopodobieństw dwóch hipotez [math]H_1[/math] i [math]H_2[/math]:
Przykłady
Celem wnioskowania statystycznego powinna być ocena prawdopodobieństwa prawdziwości hipotezy [math]H[/math] w świetle zdarzenia opisanego obserwowanymi danymi [math]D[/math], a nie odwrotnie. Mylenie tych dwóch prawdopodobieństw prowadzi np. do tzw. błędu rozumowania prokuratorskiego.
Poniższe przykłady zaczerpnięto z raportu Giuglio D'Agostini "Bayesian Reasoning in High Energy Physics - Principles and Applications".
Prawdopodobieństwo zarażenia w świetle wyników testu na HIV
Przypadkowo wybrany z populacji (w której na 60 milionów jest około stu tysięcy nosicieli wirusa) obywatel poddany jest testowi na obecność wirusa HIV. Użyty test wykrywa niemal 100% przypadków zakażenia, i daje około 0,2% „fałszywych alarmów”. Jakie jest prawdopodobieństwo, że badany obywatel jest nosicielem wirusa, jeśli test dał wynik pozytywny?
Na pierwszy rzut oka wydaje się, że skoro test wykrywa wirusa fałszywie tylko w dwu przypadkach na tysiąc, to szukane prawdopodobieństwo wynosi 1-0,2%[math]\approx[/math] 99.8%. Jednakże, jeśli wziąć pod uwagę prawdopodobieństwo a priori (zaczątek) wynoszące 100 000/60 000 000 [math]\approx[/math] 2% otrzymamy wartość bliską 50%!
Na początek wyobraźmy sobie wynik tego testu na całej populacji: będzie on pozytywny dla stu tysięcy zarażonych i dla 0,2% pozostałych, czyli w sumie 220 tysięcy. Wśród nich faktycznych nosicieli będzie tylko sto tysięcy, pozostali będą ofiarami błędu testu. Prawdopodobieństwo, że jesteśmy nosicielem, jeśli znaleźliśmy się w tej grupie, jest równe [math]\frac{100 000}{220000}\approx[/math] 45% (a nie 99,8%!).
Formalnie możemy dowieść tego wyniku korzystając z (2) i (4). Oznaczmy:
- [math]P(+)[/math] — prawdopodobieństwo pozytywnego wyniku testu,
- [math]P(HIV)[/math] — prawdopodobieństwo, że badany jest nosicielem (zaczątek),
- [math]P(\overline{HIV})[/math] — prawdopodobieństwo, że badany nie jest nosicielem (również zaczątek).
Z opisu przykładu dostaniemy:
[math]P(+|HIV)\approx 1[/math],
[math]P(+|\overline{HIV})=0,002[/math],
[math]P(HIV)= \frac{100 000}{60 000 000} = \frac{1}{600}[/math]
[math]P(\overline{HIV}) \approx 1[/math].
Szukamy [math]P(HIV|+)[/math]:
[math]\begin{matrix} P(HIV|+)& =& \frac{P(+|HIV)P(HIV)}{P(+)}\\ P(\overline{HIV}|+)& = &\frac{P(+|\overline{HIV})P(\overline{HIV})}{P(+)}\\ \frac{P(HIV|+)}{P(\overline{HIV}|+)}&=&\frac{P(+|HIV)P(HIV)}{P(+|\overline{HIV})P(\overline{HIV})} = \frac{1 \cdot \frac{1}{600}}{0,002 \cdot 1} = \frac{1}{1,2}. \end{matrix}[/math]
Ponieważ [math]P(HIV|+) + P(\overline{HIV}|+) = 1[/math], dostajemy [math]P(HIV|+) \approx 0.455[/math], czyli ok. 45%
Uaktualnianie prawdopodobnieńswa zaczątkowego czyli Bayes w barze
Spotykamy w barze znajomego, który proponuje prostą grę losową: za drinki płaci ten, kto wyciągnie z zakrytej talii niższą kartę. Zgadzamy się wierząc w losowość gry (czyli uczciwość znajomego, który grę prowadzi), ale jeśli przegramy kilka razy z rzędu zaczynamy wątpić. Opiszmy to liczbami:
Na początku przyjmujemy, że znajomy proponuje uczciwą grę losową, z prawdopodobieństwem na przykład [math]P_0(U)=0.95[/math]. Poziom naszej początkowej wiary z możliwość przeciwną, czyli że jeteśmy oszukiwani, wynosi wtedy [math]P_0(O)=0.05[/math]. Dla uproszczenia załóżmy, że jeśli prowadzący grę znajomy oszukuje, to zawsze wygra, czyli prawdopodobieństwo wygrania w każdej z gier wyniesie wtedy [math]P(W|O)=1[/math]. Jeśli gra byłaby uczciwa (losowa), to prawdopodobieństwo wygrania w każdej grze wynosiłoby [math]0.5[/math], czyli [math]P(W|U)=2^{-1}[/math]. Jeśli kolejne gry są zdarzeniami niezależnymi, to prawdopodobieństwo wygrania w [math]n[/math] kolejnych grach wyniesie [math]P(W_n|U)=2^{-n}[/math].
Ostatecznie
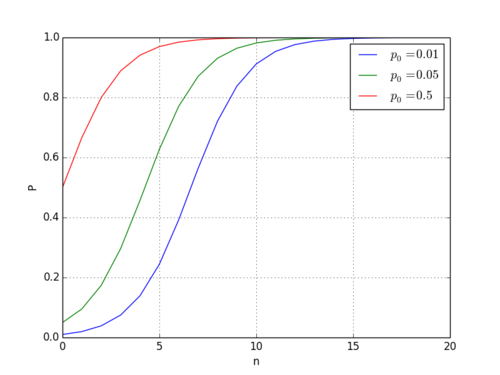
[math] P(O|W_n)=\frac{ P(W_n|O) P_0(O) }{ P(W_n|O) P_0(O) + P(W_n|U) P_0(U) } [/math]
[math]
P(O|W_n)=\frac{P_0(O) }{ P_0(O) +2^{-n} [1 - P_0(O)] }
[/math]
| kod |
import matplotlib.pyplot as plt
import numpy
t = numpy.arange(0, 20.0, 1.0)
def p(n,p0c):
return p0c/(p0c+(1-p0c)*0.5**n)
plt.plot(t, p(t, 0.01), label='$p_0=0.01$')
plt.plot(t, p(t, 0.05), label='$p_0=0.05$')
plt.plot(t, p(t, 0.5), label='$p_0=0.5$')
plt.xlabel('n')
plt.ylabel('P')
plt.grid(True)
plt.legend()
plt.show()
|
|
Referencja
Polecam doskonały tekst Giuglio D'Agostini z 1995 roku pt. "Probability and Measurement Uncertainty in Physics — a Bayesian Primer", dostępny z https://arxiv.org/abs/hep-ph/9512295