WnioskowanieStatystyczne/Z komputerem
Wnioskowanie_Statystyczne_-_wykład
Spis treści
Statystyka — z komputerem zamiast wzorów
Statystyka jest sztuką wyciągania wniosków na podstawie niepełnych danych (dostępnych doświadczeń); każdy z nas jest statystykiem, lepszym lub gorszym. Na co dzień podejmujemy decyzje — na przykład: czy szybciej dojedziemy do celu krótszą trasą przez centrum miasta, czy dłuższą, na której jednak zwykle nie ma korków? Decyzji takiej zwykle nie da się oprzeć na całkowicie ścisłym rozumowaniu, gdyż czas przejazdu zależy od wielu nieprzewidywalnych czynników. Mimo to staramy się ocenić, która trasa będzie lepsza — na podstawie doświadczenia („jeżdżę tą trasą od lat i rzadko trafiam na korki”) i/lub dodatkowych informacji („piątek po południu, trasa wylotowa z miasta… będzie tłok”). Przy tym jesteśmy świadomi, że nie będzie to ocena dokładna, tylko w najlepszym razie dość prawdopodobna.
Jak widać, intuicyjnie używamy nawet pojęcia prawdopodobieństwa… Mimo to prawie każdy, kto zetknął się z kursem statystyki, uznaje ją za dział wiedzy wysoce odległy od intuicji, skomplikowany i w dużej mierze niezrozumiały.
Dlaczego? Niestety, klasyczne teorie statystyczne po prostu takie są: skomplikowane, oparte na dalekich od intuicji i kontrowersyjnych założeniach. Co gorsza, ich poprawne zastosowanie bywa przez to trudnym zadaniem. Na szczęście w większości przypadków teorię można dziś zastąpić praktyką, czyli zdroworozsądkowymi metodami oceny szans (nie musimy ich nawet nazywać prawdopodobieństwem) za pomocą komputerów. Monte Carlo i repróbkowanie (czyli resampling, a w tym bootstrap i testy permutacyjne) to proste metody, które opiszemy w tej książce w całości bez używania wzorów. Mimo prostoty można nimi efektywnie zastąpić wiele skomplikowanych metod klasycznych. Zacznijmy od Monte Carlo.
Hazard symulowany
W grach hazardowych wszystko zależy od szczęścia... Wszystko? W takim razie dlaczego kasyna (albo toto-lotek) nie bankrutują? Zdarza się, że muszą wypłacić wielkie wygrane, ale „na dłuższą metę wychodzą na swoje".
Wiadomo, że większą szansę (czyli prawdopodobieństwo trafienia) mamy na karetę „z ręki” w pokerze niż na szóstkę w toto-lotku. A skąd to wiemy? Na pewno wśród znajomych mamy wielu, którym trafiły się cztery karty jednego nominału w rozdaniu pokera (jeśli tylko w pokera grywali), a o kimś, kto trafił szóstkę w toto-lotku zwykle w najlepszym razie słyszeliśmy (bo loterie to podatek płacony przez ludzi nie rozumiejących statystyki). Taki sposób oceny prawdopodobieństwa — na podstawie doświadczeń — jest najpewniejszy. Jednak nie zawsze dysponujemy wystarczającą liczbą doświadczeń, aby ocenić szanse wygranej; wyobraźmy sobie dla przykładu nową grę, w którą wcześniej nie graliśmy:
Za wpłaconą złotówkę rzucamy pięć razy kostką; jeśli wyrzucimy przynajmniej dwie szóstki, wygrywamy pięć złotych. W przeciwnym razie tracimy wpłaconą złotówkę. Warto zagrać?
Cóż, możemy spróbować: zagrajmy kilka razy i zobaczmy, czy się wzbogaciliśmy czy nie...
A może by tak spróbować „na sucho”, nie ryzykując pieniędzy? Doskonały pomysł! Jeżeli tylko wierzymy, że w prawdziwej grze będziemy rzucać „uczciwą”, czyli w pełni symetryczną kostką, która z równym prawdopodobieństwem ląduje na każdej z sześciu ścianek — możemy całą grę zasymulować. Znajdujemy kostkę i rzucamy: pięć rzutów, jedna szóstka — „przegraliśmy”. Następna symulowana gra: żadnej szóstki. Trzecia... widać, że trzeba do sprawy podejść systematycznie.
Wykonajmy na przykład sto eksperymentów: rzucamy kostką pięć razy, i jeśli wyrzuciliśmy przynajmniej dwie szóstki, zapisujemy „wygraną".
(...)
Trochę to było męczące, ale w końcu mamy: na sto zasymulowanych gier „wygraliśmy” 18, czyli 18 uzyskać w stu prawdziwych grach — poznaliśmy go nie ryzykując. Policzmy więc: za sto gier wpłacilibyśmy 100 zł, a dostali [math]18\cdot 5=90[/math], czyli przegralibyśmy 10 zł.
Dzięki symulacji uniknęliśmy straty, ale czy ostateczny wniosek brzmi „nie warto grać”? Żeby „wyjść na swoje” trzeba wygrać przynajmniej 20 razy na 100, a w symulacji wygraliśmy 18... a może gdyby powtórzyć tę symulację jeszcze raz, wylosowalibyśmy więcej niż 20 wygranych na 100, czyli odnieślibyśmy sukces? Trzeba by spróbować, może kilka razy po sto razy po pięć rzutów kostką, zapisać... nie! Najwyższy czas użyć komputera!
Jak zmusić komputer do rzucania kostką
Nie jest to specjalnie trudne, lecz nie da się ukryć, że wymaga trochę lepszego zaznajomienia z komputerem niż napisanie listu. Konieczny jest jakikolwiek język programowania, pozwalający korzystać z dwóch elementów: pętli i generatora liczb losowych. Może to być kompilator dowolnego „klasycznego” języka programowania (C, Pascal, Java etc.), lub interpreter możliwie prostego języka, zawierającego wymienione elementy. Interpretery języków spełniających ten warunek zawarte są coraz częściej w programach powszechnego stosowania (np. w pakietach biurowych), jak również we wszystkich „poważniejszych” środowiskach obliczeniowych („Matlab”, „Mathematica” etc.). Wreszcie istnieją specjalizowane programy do obliczeń tego typu (np. Resampling Stats).
Symulacja rzutów monetą
Na początek spróbujmy skłonić komputer do symulacji rzutów monetą. Wykorzystamy do tego „generator liczb losowych”, który losuje liczby zwykle spomiędzy zero i jeden. Robi to w taki sposób, że wylosowanie każdej z liczb z tego przedziału jest równie prawdopodobne, a wynik konkretnego losowania w żaden sposób nie zależy od wyniku losowań poprzednich (losowania niezależne).[1] Jeśli wylosowanie „każdej” liczby spomiędzy 0 i 1 jest równie prawdopodobne, to w szczególności wylosowanie liczby mniejszej niż [math]\frac{1}{2}[/math] powinno być tak samo prawdopodobne, jak wylosowanie liczby większej niż [math]\frac{1}{2}[/math]. Co to znaczy „równie prawdopodobne”? To samo, co mamy na myśli mówiąc, że w rzucie symetryczną monetą wyrzucenie orła jest równie prawdopodobne jak wyrzucenie reszki.
Czyli wystarczy umówić się, że wylosowanie liczby mniejszej od [math]\frac{1}{2}[/math] to orzeł, a większej (lub równej) — reszka. Do symulacji będziemy jeszcze potrzebować instrukcji pętli, bądź dowolnego innego mechanizmu pozwalającego na wygodne powtarzanie fragmentów programu. Jeśli już wiemy, jak to zrobić, możemy przystąpić do napisania krótkiego programu realizującego przepis (czyli algorytm) symulacji stu rzutów monetą — na przykład tak, jak w tabeli %i 1.
Zapis „reszki=reszki+1” oznacza zwiększenie zmiennej „reszki” o jeden — tak zwykle zapisujemy tę operację w popularnych językach programowania. Jeśli potraktować to dosłownie jako równanie z niewiadomą reszki, dostajemy zdanie fałszywe (albo reszki=[math]\infty[/math]).
reszki = 0
powtarzaj 100 razy:
wylosuj x
jeśli x mniejszy niż 1/2
reszki = reszki + 1
wypisz reszki
Za każdym razem, gdy uruchomimy ten program, możemy uzyskać inny wynik (oczywiście Twoje wyniki będą pewnie inną sekwencją liczb (taka jest idea generatora liczb losowych). (reszki): np. 46, 52, 44, 46... Wyniki o podobnym rozrzucie powinniśmy uzyskać w stu rzutach „prawdziwą” (symetryczną) monetą. Czyli zamiast rzucać monetą, możemy kazać komputerowi powtarzać prosty fragment programu. Wynika stąd zasadnicza korzyść, gdyż komputer potrafi powtarzać proste operacje bez porównania szybciej niż człowiek. Milion rzutów monetą? Proszę bardzo, zamieniamy w powyższym programie 100 na 1000000 i... wynik pojawia się szybciej niż zdołalibyśmy zapisać rezultat jednego rzutu monetą.
Jeśli udało nam się zmusić komputer do wykonania powyższych prostych symulacji i widzimy ich związek z fizycznym eksperymentem polegającym na rzucaniu monetą, to znaczy, że mamy już za sobą właściwie wszystkie większe problemy — ideowe i praktyczne.
Symulacja rzutów kostką
Symulacja rzutów kostką będzie tylko trochę bardziej skomplikowana: dzielimy przedział między zerem i jedynką na sześć równych części, i każdej z nich przypisujemy jeden z możliwych wyników, na przykład: od zera do [math]\frac{1}{6}[/math] — jedno oczko, od [math]\frac{1}{6}[/math] do [math]\frac{2}{6}[/math] — dwa oczka, i tak dalej. Aby upewnić się, że wyrzucenie każdej liczby oczek jest w tej symulacji faktycznie równie prawdopodobne, najwygodniej będzie skorzystać z graficznej prezentacji wyników — prosty dostęp do funkcji graficznej prezentacji danych oferuje większość wspomnianych programów, jedynie w przypadku tradycyjnych języków programowania wymagałoby to napisania specjalnego fragmentu kodu lub skorzystania z gotowej biblioteki.
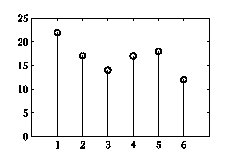
I tak, wynik stu rzutów kostką — na przykład: 22 jedynki, 17 dwójek, 14 trójek, 17 czwórek, 18 piątek i 12 szóstek — możemy przedstawić jak na rys. %i 1.
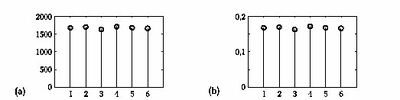
Jeśli będziemy powtarzać po dziesięć tysięcy rzutów kostką, możemy otrzymać wyniki podobne jak na rysunku %i 2(a). Zamiast liczby wystąpień każdego z wyników możemy rysować proporcje ich występowania (po podzieleniu przez całkowitą liczbę rzutów), jak na rysunku %i 2(b).
Skoro wyświetlamy proporcje, czyli prawdopodobieństwa wyrzucenia każdej liczby oczek, możemy już porównywać wyniki otrzymane dla różnych ilości powtórzeń (rzutów) — na przykład stu, dziesięciu tysięcy i miliona — jak na rysunku %i 3.
Widać, że w każdym przypadku otrzymane dla każdej liczby oczek prawdopodobieństwa są bliskie [math]\frac{1}{6}[/math] (czyli 0,166...) — zgodnie ze zdrowym rozsądkiem, skoro mamy do czynienia z sześcioma równie prawdopodobnymi możliwościami, tak właśnie powinno być. Rozumowanie to nazywa się klasyczną (bądź częstościową) definicją prawdopodobieństwa}; ścisłe sformułowanie znajduje się w rozdziale o prawdopodobieństwie. Ponadto, im więcej powtórzeń eksperymentu, tym wyniki bliższe „teoretycznej” [math]\frac{1}{6}[/math].
Ten wniosek nazywa się Prawem Wielkich Liczb. Dla miliona dostajemy już prawie dokładnie jednakowe wartości, toteż możemy powiedzieć, że prawy rysunek dobrze przybliża teoretyczny „rozkład prawdopodobieństwa” wyników rzutu kostką — czyli jednakowe prawdopodobieństwo każdego wyniku od 1 do 6.
Oceniamy szanse
Skoro już sprawdziliśmy, że komputer prawidłowo rzuca kostką, możemy wrócić do pytania postawionego na początku rozdziału.
Przede wszystkim powinniśmy nieco inaczej sformułować problem. Odpowiedź na pytanie „czy warto” może zależeć od zbyt wielu, częściowo subiektywnych, czynników. Ale na pewno jednym z nich powinna być szansa wygranej! Tak więc zamiast „czy warto zagrać” możemy zapytać o szansę (prawdopodobieństwo) wygranej:
Jaka jest szansa wyrzucenia co najmniej dwóch szóstek w pięciu rzutach kostką?
Do dzieła. Skoro potrafimy już wykorzystać komputer do symulacji rzutów kostką, wystarczy tylko tak zmodyfikować program, żeby zliczał ilość szóstek w każdych pięciu rzutach i wypisywał liczbę sukcesów (czyli wyrzucenia dwóch lub więcej szóstek) — na przykład tak jak w tabeli %i 2, symulując sto „gier”.
sukcesy = 0
powtarzaj 100 razy:
szóstki = 0
powtarzaj 5 razy:
wylosuj x
jeśli x większy niż 5/6
szóstki = szóstki + 1
jeśli szóstki > 1
sukcesy=sukcesy + 1
wypisz sukcesy/100
Kolejne wyniki mogą wyglądać tak: 19, 21, 27, 19, 19, 21, 16, 20, 11,
15... Widać spory rozrzut — między 11 a 27 wygranych na sto gier
występuje spora różnica — można wygrać, można przegrać... no ale
jak to jest w końcu z tym prawdopodobieństwem?
Zgodnie ze zdrowym rozsądkiem i intuicją (a także zgodnie z częstościową definicją prawdopodobieństwa)
prawdopodobieństwo wygranej możemy określić jako liczbę sukcesów podzieloną przez całkowitą liczbę gier, jeśli liczba gier jest duża.
Zamieńmy więc w programie z tabeli %i 2 liczbę 100 na przykład na milion. Tym razem wykonanie programu trwa już zauważalną chwilę; dostajemy, dajmy na to, 195921 wygranych na milion gier, czyli prawdopodobieństwo około 0,196 (w tym stosunkowo prostym przypadku, wybranym dla ilustracji metody, możliwe jest dokładne znalezienie wartości tego prawdopodobieństwa — wynosi ona 0,1962 (z dokładnością do czwartego miejsca po przecinku), i jest wyprowadzona w rozdziale o prawdopodobieństwie). Wynik ten jest bliski średniej wartości wyników poprzednich uzyskiwanych dla 100 powtórzeń, i mniejszy od granicznej wartości 0,2. Przypomnijmy, że aby zyskać więcej niż włożyliśmy trzeba wygrać więcej niż 20 To wskazuje, że w tej grze mamy szansę raczej przegrać niż wygrać, ale znowu nie wiadomo dokładnie jaką szansę.
Powtórzmy w takim razie eksperyment z milionem gier; dostaniemy np. 196275, 195961, 196676 (...) wygranych, czyli prawdopodobieństwa ok. 0,196-0,197. Widać, że możliwe proporcje wygranych (czyli prawdopodobieństwa) zależą silnie od liczby powtórzeń: dla stu gier dostawaliśmy proporcje wygranych najczęściej między 0,1 a 0,3, a dla miliona różnice występują dopiero na trzecim miejscu po przecinku.[2]
Ale wróćmy do postawionego problemu: jak widać z dotychczasowych wyników, w milionie gier raczej na pewno wyjdziemy „na minus", ale np. w stu grach mamy duże szanse wygrać więcej niż graniczne 20, gdyż rozrzut obserwowanych wyników symulacji jest znacznie większy. Mamy tu do czynienia z typowym dla wnioskowania statystycznego procesem, którego zasadniczą i niekoniecznie najłatwiejszą częścią jest prawidłowe sformułowanie pytania, na jakie statystyka ma odpowiedzieć. Przeformułujmy więc pytanie o wynik po raz kolejny, odnosząc je do konkretnej sytuacji np. stu gier:
jaka jest szansa, że w stu grach wygramy więcej niż wpłaciliśmy?
W analizowanym przypadku szansa ta związana jest z rozrzutem wyników, czyli liczbą wygranych w 100 grach. Rozrzut wyników możemy ocenić oglądając ich rozkład — interesuje nas rozkład liczby wygranych w stu grach. Jeden wynik symulacji (według programu z tabeli %i 2) będzie określał liczbę sukcesów w jednej z możliwych realizacji „eksperymentu", polegającego na symulacji stu gier.
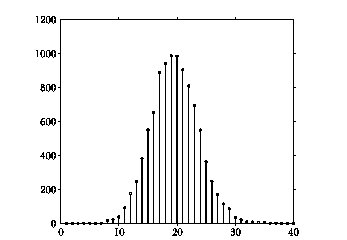
Dla przypomnienia: jedna gra polega na pięciu rzutach kostką, wpłacamy 1 zł, w przypadku wyrzucenia przynajmniej dwóch szóstek wygrywamy 5 zł. Realizujący tę symulację algorytm, zawarty w tabeli %i 2, za każdym uruchomieniem podaje jeden wynik takiej symulacji stu gier. Wynik jednego uruchomienia będziemy traktować jako jedną z liczb, których rozrzut chcemy oglądać. Oczywiście w praktyce dodajemy do programu z tabeli %i 2 jeszcze jedną zewnętrzną pętlę, w której zapamiętujemy wynik każdego z eksperymentów — ale to już szczegół techniczny. Jeśli wygenerujemy takich liczb dziesięć tysięcy, to ich rozkład może wyglądać tak, jak na rysunku %i 4.
Jeden obraz bywa wart więcej niż tysiąc słów, a jeden wykres więcej niż tysiąc liczb: rysunek %i 4 przedstawia dziesięć tysięcy liczb. Jak na dłoni widać, że większość wyników gromadzi się między 10 a 30 — w zdecydowanej większości przypadków powinniśmy wygrać pomiędzy dziesięć a trzydzieści gier ze stu.
Aby odpowiedzieć na pytanie o szansę finansowego sukcesu (przy ustalonej stawce) w stu grach, należy zliczyć liczbę symulacji, w których „wygraliśmy" więcej niż 20 gier na 100 (bo przy dwudziestu wychodzimy „na zero"), i podzielić przez 10 000. Dostajemy około 0,4 — i to jest wreszcie właściwe przybliżenie szukanego prawdopodobieństwa wygrania więcej niż wpłacimy w stu grach. Również w tym przypadku dokładną wartość możemy wyznaczyć analitycznie; wynosi ona 0,4034.
Dysponując danymi przedstawionymi na rysunku %i 4 możemy też oszacować szanse innych wyników — na przykład „czarnego scenariusza", określonego jako strata więcej niż połowy włożonej sumy. Będzie tak w przypadku, gdy na sto gier wygramy mniej niż dziesięć. Wartości te znajdują się na lewo od wartości 10; jest ich tak mało, że dokładną liczbę trudno odczytać bezpośrednio z rysunku. Korzystając z danych wygenerowanych przez program odczytujemy, że takich przypadków było 30 na 10 000, czyli prawdopodobieństwo „czarnego scenariusza” jest mniejsze niż 0,3%. A szansa, że w ogóle nie przegramy, czyli wygramy przynajmniej tyle, ile wpłacimy w stu grach? Odpowiada liczbie symulacji, w których wygraliśmy nie mniej niż 20 gier na 100, czyli sumie wartości na prawo od 20 (włącznie z 20). W tym przypadku jest to wartość bardzo bliska 50.
„Prawdziwe” Monte Carlo
W rozdziale tym poznaliśmy prostą i intuicyjną metodę pozwalającą na rozwiązywanie wielu problemów z zakresu prawdopodobieństwa i statystyki. Problem wymyślony dla ilustracji tego podejścia posiada również dokładne rozwiązanie metodami „tradycyjnej” statystyki, które możemy uzyskać kosztem dużo mniejszej ilości obliczeń, z użyciem dużo większej wiedzy. Jednak Monte Carlo nie jest bynajmniej metodą wyłącznie dla „matematycznie leniwych". Poniższy fragment pochodzi ze wspomnień wybitnego polskiego matematyka Stanisława Ulama (ten fragment wspomnień odnosi się do okresu 1946-49, gdy Ulam pracował w Los Alamos nad bombą wodorową):
(...) Pomysł ten, nazwany później metodą Monte Carlo, wpadł mi do głowy, kiedy podczas choroby stawiałem pasjanse. Zauważyłem, że znacznie praktyczniejszym sposobem oceniania prawdopodobieństwa ułożenia pasjansa (takiego jak Canfield, gdzie umiejętności gracza nie mają większego znaczenia) jest wykładanie kart, czyli eksperymentowanie z tym procesem i po prostu zapisywanie procentu wygranych, niż próba obliczenia wszystkich możliwości kombinatorycznych, których liczba rośnie wykładniczo i jest tak wielka, że pominąwszy najprostsze przypadki, jej oszacowanie jest niemożliwe. Jest to zaskakujące z intelektualnego punktu widzenia, i choć może nie całkiem upokarzające, to jednak zmusza do skromności i pokazuje granice tradycyjnego, racjonalnego rozumowania. Jeśli problem jest wystarczająco złożony, próbowanie jest lepszym sposobem niż badanie wszystkich łańcuchów możliwości.
<references>
- ↑ Tak naprawdę to komputery potrafią generować liczby zaledwie pseudo -losowe, czyli pochodzące z ciągów, które z dobrą dokładnością spełniają podane założenia — punkt startowy takiego ciągu wybieramy np. na podstawie aktualnego czasu. Prawdziwe liczby losowe mogą być generowane tylko przez prawdziwie fizyczne (nie symulowane) procesy, jak np. rozpad promieniotwórczy. Bliższe informacje o generatorach liczb pseudolosowych można znaleźć np. w książce Roberta Wieczorkowskiego i Ryszrada Zielińskiego „Komputerowe generatory liczb losowych”.
- ↑ Po raz kolejny natrafiamy na konsekwencję Prawa Wielkich Liczb. Jak widać, im więcej wyników przybliżających tę samą wielkość uśrednimy, tym większą dokładność (mniejszy rozrzut) uzyskujemy. Można udowodnić (równania XXXX), że rozrzut ten będzie odwrotnie proporcjonalny do pierwiastka liczby uśrednianych wyników.