WnioskowanieStatystyczne/Prawdopodobienstwo: Różnice pomiędzy wersjami
| (Nie pokazano 5 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 23: | Linia 23: | ||
<math> P(E)=\frac{M}{N}.</math> | <math> P(E)=\frac{M}{N}.</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
====Przykład==== | ====Przykład==== | ||
| Linia 142: | Linia 84: | ||
??? | ??? | ||
| − | Co się nie zgadza? Przykład ten nie podważa bynajmniej idei | + | Co się nie zgadza? Przykład ten nie podważa bynajmniej idei geometrycznej interpretacji prawdopodobieństwa w ogóle; po prostu wynik zależy od przepisu na "przypadkowe" przeprowadzenie cięciwy — każde z rozwiązań zakłada losowanie według równomiernego rozkładu innego parametru (położenia punktu na prostej, położenia punktu wewnątrz okręgu, kąta). Można więc powiedzieć, że problem nie został ściśle sformułowany. |
| − | geometrycznej interpretacji prawdopodobieństwa w ogóle; po prostu | ||
| − | wynik zależy od przepisu na "przypadkowe" przeprowadzenie cięciwy — | ||
| − | każde z rozwiązań zakłada losowanie według równomiernego rozkładu | ||
| − | innego parametru (położenia punktu na prostej, położenia punktu | ||
| − | wewnątrz okręgu, kąta). Można więc powiedzieć, że problem nie został | ||
| − | ściśle sformułowany. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ==== | + | ===Aksjomatyczna definicja prawdopodobieństwa=== |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Jak widać, w częstościowej definicji wykorzystane jest definiowane pojęcie (w | |
| − | + | odniesieniu do "równie prawdopodobnych" wyników), co z punktu widzenia | |
| + | teorii jest niewątpliwie poważnym defektem. Można go uniknąć, | ||
| + | wprowadzając prawdopodobieństwo jako liczbę spełniającą po prostu | ||
| + | poniższe aksjomaty (aksjomatyczna definicja | ||
| + | prawdopodobieństwa<ref>Podana przez Kołmogorowa w roku 1933.</ref>): | ||
| + | <equation id="eq:42"> | ||
| + | <math> | ||
| + | P(A)\geq 0 | ||
| + | </math> | ||
| + | </equation> | ||
| + | <equation id="eq:43"> | ||
| + | <math> | ||
| + | P(\Omega )=1 | ||
| + | </math> | ||
| + | </equation> | ||
| − | <math> P(A)=P(A | + | jeśli A i B wykluczają się nawzajem, to |
| + | <equation id="eq:44"> | ||
| + | <math> | ||
| + | P(A\cup B)=P(A)+P(B) | ||
| + | </math> | ||
| + | </equation> | ||
| − | + | Oznaczmy symbolem <math>\overline{A}</math> dopełnienie zdarzenia | |
| − | + | <math>A</math> do przestrzeni <math>\Omega</math>. Wtedy <xr | |
| − | + | id="eq:42">(%i)</xr> i <xr id="eq:43">(%i)</xr> implikują: | |
| − | |||
<math> | <math> | ||
| − | + | 1=P(\Omega )=P(A\cup \overline{A})=P(A)+P(\overline{A}) | |
| − | P( | + | </math> |
| − | czyli | + | czyli |
| − | + | <equation id="eq:45"> | |
| − | + | <math> | |
| − | + | \ 0\leq P(A)\leq 1 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | <equation id="eq: | ||
| − | <math> | ||
</math> | </math> | ||
</equation> | </equation> | ||
| − | + | (Ten wniosek bywa dołączany jako czwarty aksjomat.) | |
| − | + | ||
| − | + | Ta definicja jest już formalnie poprawna, jednak nie dostarcza żadnego | |
| − | + | przepisu na sposób obliczania definiowanej wielkości, co uniemożliwia | |
| − | + | jej praktyczne zastosowanie. Z kolei różne od klasycznego, | |
| − | + | [[WnioskowanieStatystyczne/Twierdzenie Bayesa|Bayesowskie podejście do statystyki określa | |
| − | + | prawdopodobieństwo jako miarę wiary w możliwość wystąpienia danego | |
| + | zdarzenia]] — jego obliczanie również bywa niełatwe. | ||
| + | Pojęcie prawdopodobieństwa leży u podstaw klasycznej teorii | ||
| + | statystyki, stąd problemy z jego ścisłą definicją mogą rzucać cień na | ||
| + | wiarę w jej spójność. Z drugiej strony, jak zauważa [http://www.juliansimon.com/writings/Resampling_Philosophy/ J.L. Simon]: | ||
| − | + | <blockquote> | |
| + | (...) dyskusja ta przypomina kontrowersje wokół pojęcia | ||
| + | czasu (czym czas naprawdę "jest"), które powstrzymywały postęp w | ||
| + | fizyce, dopóki Einstein nie powiedział, że czas powinniśmy zdefiniować | ||
| + | po prostu jako to, co odczytuje się z zegara. | ||
| + | </blockquote> | ||
Aktualna wersja na dzień 06:09, 3 cze 2022
Wnioskowanie_Statystyczne_-_wykład
Spis treści
Definicje prawdopodobieństwa
Częstościowa definicja prawdopodobieństwa
Niech eksperyment [math]\Omega [/math] ma [math]N[/math] "równie prawdopodobnych" wyników [math]A_{i}[/math]:
[math] \Omega =A_{1},A_{2},...A_{N}. [/math]
Jeśli zdarzenie [math]E[/math] określone jest przez podzbiór przestrzeni [math]\Omega[/math] o liczebności [math]M[/math]
[math] E=A_{1}\cup A_{2}...\cup A_{M} [/math]
to prawdopodobieństwo zdarzenia [math]E[/math] określamy jako
[math] P(E)=\frac{M}{N}.[/math]
Przykład
Spróbujmy określić prawdopodobieństwo zdarzenia, że poprowadzona w sposób przypadkowy cięciwa okręgu będzie miała długość większą od promienia.
Rozwiązanie:
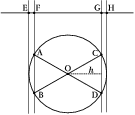
Jak "przypadkowo" poprowadzić cięciwę? Narysujmy dowolną prostą i wybierzmy na niej losowo punkt. Przez ten punkt prowadzimy prostopadłą, której punkty przecięcia z okręgiem będą wyznaczać cięciwy. Oczywiście nie wszystkie punkty na prostej dadzą prostopadłe, które będą miały w ogóle punkty wspólne z okręgiem — tylko punkty z odcinka E–H rys.%i 1. Z tych punktów graniczną cięciwę o długości równej promieniowi będzie wyznaczał punkt F, dla którego trójkąt AOB będzie równoboczny. Analogicznie z drugiej strony dla punktu G i trójkąta COD. Tak więc wszystkie punkty z odcinka EH będą generować cięciwy, a punkty z odcinka FG — cięciwy dłuższe od promienia. Prawdopodobieństwo "wylosowania" cięciwy dłuższej niż promień będzie równe stosunkowi długości odcinka FG do EH. Jeśli pamiętamy wzór na wysokość trójkąta równobocznego, łatwo znajdziemy jego wartość: [math]\frac{\sqrt{3}} 2[/math].
Inne rozwiązanie:
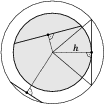
Wybieramy losowo punkt wewnątrz okręgu, i prowadzimy przez niego prostą prostopadłą do promienia przechodzącego przez ten sam punkt. Jak widać z rys.%i 2, prosta ta wyznaczy cięciwę dłuższą niż promień, jeśli punkt będzie położony w odległości mniejszej niż [math]\frac{\sqrt{3}}{2}[/math] od środka. Wyznacza to wnętrze okręgu o promieniu [math]\frac{\sqrt{3}}{2}[/math], którego pole wyniesie [math]\frac{3\pi}{4}[/math] (przyjmujemy jednostkowy promień ,,dużego okręgu). Szukane prawdopodobieństwo jest stosunkiem tej wielkości do pola ,,dużego okręgu, czyli wynosi [math]\frac{3}{4}[/math].
Jeszcze inne rozwiązanie:
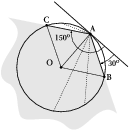
Wyznaczmy na okręgu punkt, z którego będziemy prowadzić cięciwy (punkt A na rys.%i 3). Parametrem określającym jednoznacznie cięciwę będzie kąt między styczną do okręgu w danym punkcie a jej kierunkiem, od [math]0^\circ[/math] do [math]180^\circ[/math]. Cięciwy o długości większej niż długość promienia będą wyznaczone przez kąty od [math]30^\circ[/math] do [math]150^\circ[/math] (trójkąty BOA i COA na rys.%i 3 są równoboczne). Stanowi to dwie trzecie zakresu kątów wyznaczających cięciwy, więc szukane prawdopodobieństwo wynosi [math]\frac{2}{3}[/math].
???
Co się nie zgadza? Przykład ten nie podważa bynajmniej idei geometrycznej interpretacji prawdopodobieństwa w ogóle; po prostu wynik zależy od przepisu na "przypadkowe" przeprowadzenie cięciwy — każde z rozwiązań zakłada losowanie według równomiernego rozkładu innego parametru (położenia punktu na prostej, położenia punktu wewnątrz okręgu, kąta). Można więc powiedzieć, że problem nie został ściśle sformułowany.
Aksjomatyczna definicja prawdopodobieństwa
Jak widać, w częstościowej definicji wykorzystane jest definiowane pojęcie (w odniesieniu do "równie prawdopodobnych" wyników), co z punktu widzenia teorii jest niewątpliwie poważnym defektem. Można go uniknąć, wprowadzając prawdopodobieństwo jako liczbę spełniającą po prostu poniższe aksjomaty (aksjomatyczna definicja prawdopodobieństwa[1]):
jeśli A i B wykluczają się nawzajem, to
Oznaczmy symbolem [math]\overline{A}[/math] dopełnienie zdarzenia [math]A[/math] do przestrzeni [math]\Omega[/math]. Wtedy (1) i (2) implikują:
[math] 1=P(\Omega )=P(A\cup \overline{A})=P(A)+P(\overline{A}) [/math]
czyli
(Ten wniosek bywa dołączany jako czwarty aksjomat.)
Ta definicja jest już formalnie poprawna, jednak nie dostarcza żadnego przepisu na sposób obliczania definiowanej wielkości, co uniemożliwia jej praktyczne zastosowanie. Z kolei różne od klasycznego, Bayesowskie podejście do statystyki określa prawdopodobieństwo jako miarę wiary w możliwość wystąpienia danego zdarzenia — jego obliczanie również bywa niełatwe.
Pojęcie prawdopodobieństwa leży u podstaw klasycznej teorii statystyki, stąd problemy z jego ścisłą definicją mogą rzucać cień na wiarę w jej spójność. Z drugiej strony, jak zauważa J.L. Simon:
(...) dyskusja ta przypomina kontrowersje wokół pojęcia czasu (czym czas naprawdę "jest"), które powstrzymywały postęp w fizyce, dopóki Einstein nie powiedział, że czas powinniśmy zdefiniować po prostu jako to, co odczytuje się z zegara.
- ↑ Podana przez Kołmogorowa w roku 1933.