WnioskowanieStatystyczne/Rozklady-przyklady: Różnice pomiędzy wersjami
(→Dowód) |
(→Dowód) |
||
| (Nie pokazano 17 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 296: | Linia 296: | ||
| − | <math> | + | <math> |
| − | + | \sigma ^{2}(k) = | |
| − | \sigma ^{2}(k) | + | \\[5pt] |
| − | + | = E(k^{2})-\{E(k)\}^{2} | |
\\ | \\ | ||
| − | + | = \underset{k=0}{\overset{\infty } | |
| − | + | {\sum}}k^{2}\frac{\lambda ^{k}}{k!}e^{-\lambda } -\lambda ^{2} \qquad\longleftarrow \textrm{zerowy wyraz sumy jest zerem} | |
| − | {\sum}}k^{2}\frac{\lambda ^{k}}{k!}e^{-\lambda } -\lambda ^{2} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
\\ | \\ | ||
| + | = \lambda e^{-\lambda}\underset{k=1}{\overset{\infty }{\sum }}\frac{k^2 \lambda ^{k-1}}{k(k-1)!}-\lambda ^{2} | ||
| + | \\[5pt] | ||
| + | = \lambda e^{-\lambda}\underset{k=1}{\overset{\infty }{\sum }}\frac{k\lambda ^{k-1}}{(k-1)!}-\lambda ^{2} | ||
| + | \\[5pt] | ||
| + | = \lambda e^{-\lambda}\underset{k=1}{\overset{\infty }{\sum }}\frac{\left( (k-1)+1\right)\lambda ^{k-1}}{(k-1)!}-\lambda ^{2} | ||
| + | \\[5pt] | ||
| + | = \lambda e^{-\lambda}\underset{k=1}{\overset{\infty }{\sum }}\frac{ (k-1)\lambda ^{k-1}}{(k-1)!} + | ||
| + | \lambda e^{-\lambda}\underset{k=1}{\overset{\infty }{\sum }}\frac{\lambda ^{k-1}}{(k-1)!} - | ||
| + | \lambda ^{2} | ||
| + | \\[5pt] | ||
| + | = \lambda e^{-\lambda}\underset{k=2}{\overset{\infty }{\sum }}\frac{ \lambda \lambda ^{k-2}}{(k-2)!} + | ||
| + | \lambda e^{-\lambda}\underset{k=1}{\overset{\infty }{\sum }}\frac{\lambda ^{k-1}}{(k-1)!} - | ||
| + | \lambda ^{2} | ||
| + | \\[5pt] | ||
| + | = \lambda^2 e^{-\lambda}\underset{k=2}{\overset{\infty }{\sum }}\frac{ \lambda^{k-2}}{(k-2)!} + | ||
| + | \lambda e^{-\lambda}\underset{k=1}{\overset{\infty }{\sum }}\frac{\lambda ^{k-1}}{(k-1)!} - | ||
| + | \lambda ^{2} \qquad\longleftarrow l=k-2, m=k-1 | ||
| + | \\[5pt] | ||
| + | = \lambda^2 e^{-\lambda}\underset{l=0}{\overset{\infty }{\sum }}\frac{ \lambda^{l}}{l!} + | ||
| + | \lambda e^{-\lambda}\underset{m=0}{\overset{\infty }{\sum }}\frac{\lambda ^{m}}{m!} - | ||
| + | \lambda ^{2} \qquad\longleftarrow \textrm{rozwinięcie } e^x \textrm{ w szereg Taylora wokół } x=0: e^x=\sum_{n=0}^{\infty} \frac{x^n}{n!} | ||
| + | \\[10pt] | ||
| + | = \lambda^2 e^{-\lambda } e^\lambda + \lambda e^{-\lambda} e^\lambda -\lambda^2 | ||
| + | \\[10pt] | ||
| + | = \lambda^2 + \lambda - \lambda^2 = \lambda . | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</math> | </math> | ||
| Linia 338: | Linia 344: | ||
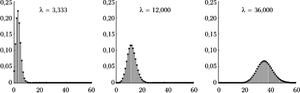
[[Plik:Rozklad_poissona.png|300px|thumb|left|<figure id="fig:rozw2"></figure>Rozkłady Poissona dla różnych wartości parametru <math>\lambda</math>.]] | [[Plik:Rozklad_poissona.png|300px|thumb|left|<figure id="fig:rozw2"></figure>Rozkłady Poissona dla różnych wartości parametru <math>\lambda</math>.]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
Aktualna wersja na dzień 19:38, 17 mar 2024
Wnioskowanie_Statystyczne_-_wykład
Spis treści
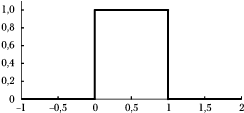
Rozkład równomierny
... zwany też jednostajnym, prostokątnym lub płaskim, przyjmuje jednakowe wartości dla wszystkich liczb z jakiegoś odcinka (na przykład między zero a jeden), a poza tym odcinkiem ma wartość zero:
[math]\begin{matrix} p(x) = 1 & \textrm{ dla } & 0\leq x\leq 1 \\ p(x) = 0 & \textrm{ dla } & x\gt 1\ \textrm{ lub }\ x\lt 0. \end{matrix}[/math]
Wartość oczekiwana
[math] \mu =E(x)=\int\limits_0^1 x dx=\left[\frac{x^{2}}{2}\right]_0^1=\frac{1}{2}. [/math]
Wariancja
[math] \sigma ^{2}=E((x-\mu )^{2})= \int\limits_0^1 \left(x-\frac 1 2 \right)^2 dx = \int\limits_0^1\left(x^2 - x +\frac 14\right) dx = \left[\frac{x^3}3 - \frac{x^2}2 +\frac x 4 \right]^1_0 = \frac 1 {12}. [/math]
Oczywiście rozkład jednostajny może być określony na dowolnym odcinku [math](a, b)[/math] — wystarczy przeskalować opisaną powyżej kanoniczną postać:
[math]\begin{matrix} p(x) = \frac{1}{b-a} & \textrm{ dla } & a\leq x\leq b \\ p(x) = 0 & \textrm{ dla } & x\lt a\ \textrm{ lub }\ x\gt b. \end{matrix}[/math]
Proste modyfikacje przytoczonych powyżej całek wykażą, że jego wartość oczekiwana wynosi
[math]\frac{a+b}{2},[/math]
a wariancja
[math]\frac{(b-a)^2}{12}[/math].
Rozkład dwumianowy
Powtarzamy [math]n[/math] razy doświadczenie o dwóch możliwych wynikach [math]A[/math] i [math]\overline{A}[/math] oraz prawdopodobieństwach odpowiednio [math]p[/math] i [math]q[/math], przy czym [math]p+q=1[/math]. Wynik [math]A[/math] nazywamy sukcesem i pytamy, jakie jest prawdopodobieństwo [math]k[/math] sukcesów?
Liczba [math]k[/math]-elementowych podciągów ciągu [math]n[/math]-elementowego wynosi [math]\frac{n!}{(n-k)!}[/math], czyli [math]n(n-1)(n-2)...(n-k+1)[/math]; na pierwszym miejscu każdego z ciągów możemy ustawić każdy z [math]n[/math] elementów, po jego ustaleniu na drugim miejscu każdy z [math]n-1[/math] elementów itd. Jeśli ponadto nie rozróżniamy podciągów o różnej kolejności elementów, to liczbę tę podzielić należy przez liczbę permutacji (przestawień) zbioru [math]k[/math]-elementowego, czyli [math]k![/math]. W rezultacie dostajemy
[math] \frac{n!}{k!(n-k)!}=\binom{n}{k}. [/math]
Niech [math]P_{n}(k)[/math] oznacza prawdopodobieństwo wystąpienia
[math]k[/math] razy zdarzenia o prawdopodobieństwie [math]p[/math] w
serii [math]n[/math] powtórzeń. Prawdopodobieństwo jednej serii
[math]k[/math] zdarzeń [math]A[/math] i [math](n-k)[/math] zdarzeń
[math]\overline{A}[/math] wynosi [math]p^k q^{(n-k)}[/math]. Zgodnie
z powyższymi rozważaniami, takich serii, które różnią się kolejnością
wystąpienia zdarzeń [math]p[/math] i [math]q[/math], będzie
[math]\binom n k[/math]. Ostatecznie rozkład dwumianowy możemy opisać
następującym wzorem:
[math] P_{n}(k)=\binom{n}{k}p^{k}q^{n-k}=\frac{n!}{k!(n-k)!}p^{k}(1-p)^{n-k}. [/math]
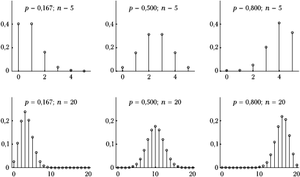
Rysunek %i 3 przedstawia rozkłady dwumianowe dla różnych wartości [math]p[/math] i [math]n[/math]. Wartość oczekiwana [math]\mu[/math] i wariancja [math]\sigma^2[/math] rozkładu dwumianowego wyrażają się następującymi wzorami:
[math] \mu=np, \qquad \sigma^2=npq. [/math]
Dowód
Bezpośrednie rachunki są w tym przypadku żmudne, więc dla znalezienia wartości oczekiwanej i wariancji rozkładu dwumianowego posłużymy się zmienną losową [math]x_{i}[/math], opisującą wynik pojedynczego doświadczenia. Przyjmuje ona wartość 1, jeśli zaszło zdarzenie [math]A[/math] (sukces) i 0 w przypadku porażki. Rozkład liczby sukcesów w serii [math]n[/math] powtórzeń opisuje zmienna będąca ich sumą [math]X=\sum\limits_{i=1}^n x_{i}[/math].
Wartość oczekiwana zmiennej [math]x_i[/math], czyli wyniku pojedynczego doświadczenia, wynosi
[math] E(x_i)=\sum\limits_i x_i P(X=x_i) = 1\cdot p + 0\cdot q = p. [/math]
Wartość oczekiwana sumy [math]n[/math] zmiennych [math]x_i[/math], dającej wartość zmiennej opisywanej rozkładem dwumianowym, będzie (z liniowości wartości oczekiwanej) sumą wartości oczekiwanych — stąd wartość oczekiwana rozkładu dwumianowego wyniesie [math]n p[/math]. Z kolei wariancja [math]x_i[/math] wynosi
[math] \sigma^2(x_i)=E((x_{i}-\mu)^{2})=\sum\limits_i (x_i-p)^2P(X=x_i)= (1-p)^{2}p+(0-p)^{2}q =q^{2}p+p^{2}q=pq(p+q)=pq. [/math]
Wariancja rozkładu dwumianowego będzie równa wariancji sumy [math]n[/math] zmiennych [math]x_i[/math]. Ponieważ zmienne te są niezależne,
[math] \sigma^2\left(\sum_{i=1}^{n}x_i\right) = n\sigma^2(x_i) = npq. [/math]
Przykład: rozkład dwumianowy
Obliczmy rozkład prawdopodobieństwa wyrzucenia [math]k[/math] szóstek w pięciu rzutach kostką (symulowany w rozdziale o metodzie Monte Carlo): [math]p=\dfrac{1}{6}[/math], [math]q=\dfrac{5}{6}[/math], [math]\binom{5}{0}=1[/math], [math]\binom{5}{1}=5[/math] i tak dalej.
| [math]k=[/math] | 0 | 1 | 2 | 3 | 4 | 5 |
| [math]P_5(k)\approx[/math] | 0,4019 | 0,4019 | 0,1608 | 0,0322 | 0,0032 | 0,0001 |
Wartości te przedstawione są na wykresie w lewym górnym rogu rysunku %i 3. Prawdopodobieństwo wyrzucenia przynajmniej dwóch (czyli od dwóch do pięciu) szóstek wynosi
Przykład: trzy dziewczynki
Obliczmy prawdopodobieństwo, że wśród czworga dzieci będą co najmniej trzy dziewczynki — zakładając, że prawdopodobieństwa urodzenia dziecka każdej płci są równe.
"Co najmniej trzy dziewczynki" można zasymulować jako cztery lub trzy "sukcesy" w czterech "losowaniach płci" o prawdopodobieństwie sukcesu [math]\frac{1}{2}[/math], czyli
zgodnie z wynikiem symulacji z zadania.
Przykład: trening koszykarski
W rzutach do kosza uzyskiwaliśmy średnio 6 trafień na 10 rzutów. Po zmianie techniki w pierwszych 10 rzutach uzyskaliśmy 9 trafień. Czy należy wnioskować, że nowa technika rzutów poprawia średnią trafień?
Jeśli zmiana techniki nie wpłynęła na skuteczność, to prawdopodobieństwo uzyskania 9 lub więcej trafień na 10 rzutów odpowiada 9 lub 10 sukcesom w 10 losowaniach o prawdopodobieństwie 0,6, czyli:
Czyli mniej niż 5% — zgodnie z wynikiem symulacji.
Rozkład Poissona
W granicy dużej liczby [math]n[/math] zdarzeń o niskim prawdopodobieństwie [math]p[/math], tj. [math]n\rightarrow \infty ,[/math] [math]np=\lambda =const., [/math] otrzymujemy z rozkładu dwumianowego rozkład Poissona:
Dowód
[math]\begin{matrix} P_{n}(k)&=&\dfrac{n!}{k!(n-k)!}p^{k}q^{n-k}= \dfrac{n!}{k!(n-k)!} \left(\dfrac{\lambda }{n}\right)^{k}\dfrac{(1-\frac{\lambda }{n})^{n}}{(1-\frac{\lambda }{n})^{k}}=\\ &=&\dfrac{\lambda ^{k}}{k!}\dfrac{n(n-1)...(n-k+1)(1-\frac{\lambda }{n})^{n}}{n^{k}(1-\frac{\lambda }{n})^{k}}= \\ &=&\dfrac{\lambda ^{k}}{k!}\left(1-\dfrac{\lambda }{n}\right)^{n}\dfrac{(1-\frac{1}{n}) (1-\frac{2}{n})...(1-\frac{k-1}{n})}{(1-\frac{\lambda }{n})^{k}}. \end{matrix}[/math]
Ponieważ
[math]\underset{n\rightarrow \infty }{\lim } \frac{(1-\frac{1}{n}) (1-\frac{2}{n})...(1-\frac{k-1}{n})}{(1-\frac{\lambda }{n})^{k}} = 1[/math]
[math]e=\underset{n\rightarrow \infty }{\lim
}(1+\frac{1}{n})^{n}[/math]
[math]\underset{n\rightarrow \infty }{\lim
}(1-\frac{\lambda }{n})^{n}=e^{-\lambda}[/math]
dostajemy [math] P_{n}(k)=P_{\lambda}(k)=\dfrac{\lambda ^{k}}{k!}e^{-\lambda }. [/math]
Sprawdźmy warunek [math]P(\Omega)=1[/math]
Przestrzeń wszystkich możliwych zdarzeń wyczerpują tu liczby sukcesów [math]k[/math] od zera do [math]n[/math] [math](n\rightarrow\infty)[/math], czyli
gdyż
Wartość oczekiwana i wariancja
wynoszą:
Dowód
[math] E(k)=\underset{k=0}{\overset{\infty }{\sum }}k\frac{\lambda ^{k}}{k!} e^{-\lambda }=\lambda e^{-\lambda }\underset{k=1}{\overset{\infty }{\sum }} \frac{\lambda ^{k-1}}{(k-1)!}=\lambda e^{-\lambda }\underset{l=0}{\overset{ \infty }{\sum }}\frac{\lambda ^{l}}{l!}=\lambda e^{-\lambda } e^{\lambda }=\lambda, [/math]
[math] \sigma ^{2}(k) = \\[5pt] = E(k^{2})-\{E(k)\}^{2} \\ = \underset{k=0}{\overset{\infty } {\sum}}k^{2}\frac{\lambda ^{k}}{k!}e^{-\lambda } -\lambda ^{2} \qquad\longleftarrow \textrm{zerowy wyraz sumy jest zerem} \\ = \lambda e^{-\lambda}\underset{k=1}{\overset{\infty }{\sum }}\frac{k^2 \lambda ^{k-1}}{k(k-1)!}-\lambda ^{2} \\[5pt] = \lambda e^{-\lambda}\underset{k=1}{\overset{\infty }{\sum }}\frac{k\lambda ^{k-1}}{(k-1)!}-\lambda ^{2} \\[5pt] = \lambda e^{-\lambda}\underset{k=1}{\overset{\infty }{\sum }}\frac{\left( (k-1)+1\right)\lambda ^{k-1}}{(k-1)!}-\lambda ^{2} \\[5pt] = \lambda e^{-\lambda}\underset{k=1}{\overset{\infty }{\sum }}\frac{ (k-1)\lambda ^{k-1}}{(k-1)!} + \lambda e^{-\lambda}\underset{k=1}{\overset{\infty }{\sum }}\frac{\lambda ^{k-1}}{(k-1)!} - \lambda ^{2} \\[5pt] = \lambda e^{-\lambda}\underset{k=2}{\overset{\infty }{\sum }}\frac{ \lambda \lambda ^{k-2}}{(k-2)!} + \lambda e^{-\lambda}\underset{k=1}{\overset{\infty }{\sum }}\frac{\lambda ^{k-1}}{(k-1)!} - \lambda ^{2} \\[5pt] = \lambda^2 e^{-\lambda}\underset{k=2}{\overset{\infty }{\sum }}\frac{ \lambda^{k-2}}{(k-2)!} + \lambda e^{-\lambda}\underset{k=1}{\overset{\infty }{\sum }}\frac{\lambda ^{k-1}}{(k-1)!} - \lambda ^{2} \qquad\longleftarrow l=k-2, m=k-1 \\[5pt] = \lambda^2 e^{-\lambda}\underset{l=0}{\overset{\infty }{\sum }}\frac{ \lambda^{l}}{l!} + \lambda e^{-\lambda}\underset{m=0}{\overset{\infty }{\sum }}\frac{\lambda ^{m}}{m!} - \lambda ^{2} \qquad\longleftarrow \textrm{rozwinięcie } e^x \textrm{ w szereg Taylora wokół } x=0: e^x=\sum_{n=0}^{\infty} \frac{x^n}{n!} \\[10pt] = \lambda^2 e^{-\lambda } e^\lambda + \lambda e^{-\lambda} e^\lambda -\lambda^2 \\[10pt] = \lambda^2 + \lambda - \lambda^2 = \lambda . [/math]
Jeśli wariancja rozkładu Poissona jest równa jego wartości oczekiwanej ([math]\lambda[/math]), to odchylenie standardowe [math]\sigma[/math] (czyli pierwiastek z wariancji) wyniesie
[math] \sigma ^{2}(k)=\lambda \Rightarrow \sigma (k)=\sqrt{\lambda }=\sqrt{np}. [/math]
Wynik ten przytaczany bywa jako "prawo" określające błąd liczby zliczeń jako jej pierwiastek.